【吴恩达课后编程作业】第三周作业 (附答案、代码)隐藏层神经网络 神经网络和深度学习
上一篇:【课程1 - 第二周作业】 ✌✌✌✌ 【目录】 ✌✌✌✌ 下一篇:【课程1 - 第三周作业】
首先说明一下,大学生一枚,最近在学习神经网络,写这篇文章只是记录自己的学习历程,起总结复习的作用,别无它意,本文参考了zsffuture的博客、布衣先生real的博客、孔小爽的博客、何宽的博客以及Github上fengdu78老师的文章进行学习
✌ 我们要实现一个能够分类样本点的神经网络
- numpy:常用数学工具库
- matplotlib:python的画图工具
- LogisticRegression:逻辑回归模型
- lightgbm:lgb模型
- cross_val_score:交叉验证
import numpy as np
import matplotlib.pyplot as plt
from testCases import *
import sklearn.datasets
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets
from sklearn.linear_model import LogisticRegression
import lightgbm as lgb
from sklearn.model_selection import cross_val_score
✌ 加载训练测试数据集
- X:特征矩阵
- Y:标签
X, Y = load_planar_dataset()
✌ 打印数据集的详细数据
print('样本数量:',X.shape[1])
print('特征数量:',X.shape[0])
print('X的维度:',X.shape)
print('Y的维度:',Y.shape)
查看输出结果:
样本数量: 400
特征数量: 2
X的维度: (2, 400)
Y的维度: (1, 400)
✌ 神经网络介绍
现在我们的准备工作已经做好了,接下来就是搭建神经网络
z = w . T ∗ X + b z=w.T*X+b z=w.T∗X+b
y = a = s i g m o i d ( z ) y=a=sigmoid(z) y=a=sigmoid(z)
单一样本的损失:
L ( y , a ) = − ( y ∗ l o g ( a ) + ( 1 − y ) ∗ l o g ( 1 − a ) ) L(y,a)=-(y*log(a)+(1-y)*log(1-a)) L(y,a)=−(y∗log(a)+(1−y)∗log(1−a))
计算所有样本的平均损失值:
J = 1 / m ∑ i = 0 m L ( y , a ) J=1/m\sum_{i=0}^mL(y,a) J=1/mi=0∑mL(y,a)
搭建神经网络的主要步骤是:
-
定义模型结构(例如输入特征的数量)
-
初始化模型的参数
-
不断迭代(调整参数):
3.1 计算当前损失(正向传播)
3.2 计算当前梯度(反向传播)
3.3 更新参数(梯度下降)
✌ 定义sigmoid函数
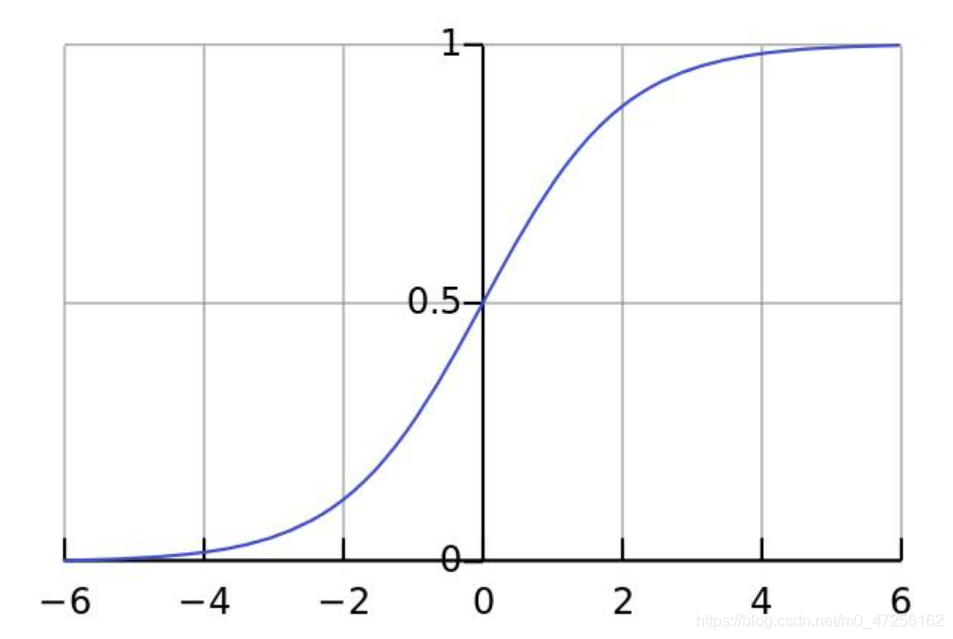
a = s i g m o i d ( z ) a=sigmoid(z) a=sigmoid(z)
s i g m o i d = 1 / ( 1 + e − x ) sigmoid=1/(1+e^-x) sigmoid=1/(1+e−x)
因为我们要做的是二分类问题,所以到最后要将其转化为概率,所以可以利用sigmoid函数的性质将其转化为0~1之间
def sigmoid(z):
"""
功能:激活函数,计算sigmoid的值
参数:
z:任何维度的矩阵
返回:
s:sigmoid(z)
"""
s=1/(1+np.exp(-z))
return s
✌ 定义各网络层的节点数
这里我们为什么要获取各个层的节点数呢?
原因是在初始化w、b等参数时需要确定其维度,以便于后面的传播计算
def layer_size(X,Y):
"""
功能:获得各个网络层的节点数
参数:
X:特征矩阵
Y:标签
返回:
in_layer:输出层的节点数
hidden_layer:隐藏层的节点数
out_layer:输出层的节点数
"""
# 本数据集为两个特征
in_layer=X.shape[0]
# 自己定义隐藏层为4个节点
hidden_layer=4
# 输出层为1维
out_layer=Y.shape[0]
return in_layer,hidden_layer,out_layer
✌ 定义初始化w、b的函数
在进行梯度下降之前,要初始化w和b的值,但是这里会有个问题,为了方便我们会把w、b的值全部初始化为0,这样做是不正确的,原因是:如果都为0,会导致在传播计算时,模型对称,各个节点的参数不起作用,可以自己推到一下
所以我们要给w、b进行随机取值
本文参数维度:
- W1:(4,2)
- b1:(4,1)
- W2:(1,4)
- b2:(1,1)
def init_w_b(in_layer,hidden_layer,out_layer):
"""
功能:初始化w,b的维度和值
参数:
in_layer:输出层的节点数
hidden_layer:隐藏层的节点数
out_layer:输出层的节点数
返回:
init_params:对应各层参数的字典
"""
# 定义随机种子,以便之后每次产生随机数唯一
np.random.seed(2021)
# 初始化参数,符合高斯分布
W1=np.random.randn(hidden_layer,in_layer)*0.01
b1=np.random.randn(hidden_layer,1)
W2=np.random.randn(out_layer,hidden_layer)*0.01
b2=np.random.randn(out_layer,1)
init_params={
'W1':W1,
'b1':b1,
'W2':W2,
'b2':b2}
return init_params
✌ 定义向前传播函数
神经网络分为正向传播和反向传播
正向传播计算求出损失函数,然后反向计算各个梯度
然后进行梯度下降,更新参数
计算公式:
Z 1 = W 1 ∗ X + b 1 Z1=W1*X+b1 Z1=W1∗X+b1
A 1 = t a n h ( Z 1 ) A1=tanh(Z1) A1=tanh(Z1)
Z 2 = W 2 ∗ A 1 + b 2 Z2=W2*A1+b2 Z2=W2∗A1+b2
A 2 = s i g m o i d ( Z 2 ) A2=sigmoid(Z2) A2=sigmoid(Z2)
def forward(W1,b1,W2,b2,X,Y):
"""
功能:向前传播,计算出各个层的激活值和未激活值(A1,A2,Z1,Z2)
参数:
W1:隐藏层的权值参数
b1:隐藏层的偏置参数
W2:输出层的权值参数
b2:输出层的偏置参数
X:特征矩阵
Y:标签
返回:
forward_params:对应各层数据的字典
"""
# 计算隐藏层
Z1=np.dot(W1,X)+b1
# 激活
A1=np.tanh(Z1)
# 计算第二层
Z2=np.dot(W2,A1)+b2
# 激活
A2=sigmoid(Z2)
forward_params={
'Z1':Z1,
'A1':A1,
'Z2':Z2,
'A2':A2,
'W1':W1,
'b1':b1,
'W2':W2,
'b2':b2}
return forward_params
✌ 定义损失函数
损失函数为交叉熵,数值越小,表明模型越优秀
计算公式:
J ( W 1 , b 1 , W 2 , b 2 ) = 1 / m ∑ i = 0 m − ( y ∗ l o g ( A 2 ) + ( 1 − y ) ∗ l o g ( 1 − A 2 ) ) J(W1,b1,W2,b2)=1/m\sum_{i=0}^m-(y*log(A2)+(1-y)*log(1-A2)) J(W1,b1,W2,b2)=1/mi=0∑m−(y∗log(A2)+(1−y)∗log(1−A2))
def loss_fn(W1,b1,W2,b2,X,Y):
"""
功能:构造损失函数,计算损失值
参数:
W1:隐藏层的权值参数
b1:隐藏层的偏置参数
W2:输出层的权值参数
b2:输出层的偏置参数
X:特征矩阵
Y:标签
返回:
loss:模型损失值
"""
# 样本数
m=X.shape[1]
# 向前传播,获取激活值A2
forward_params=forward(W1,b1,W2,b2,X,Y)
A2=forward_params['A2']
# 计算损失值
loss=np.multiply(Y,np.log(A2))+np.multiply(1-Y,np.log(1-A2))
loss=-1/m*np.sum(loss)
# 降维,如果不写,可能会有错误
loss=np.squeeze(loss)
return loss
✌ 定义向后传播函数
反向计算各个梯度
然后进行梯度下降,更新参数
计算公式:
d Z 2 = A 2 − Y dZ2=A2-Y dZ2=A2−Y
d W 2 = 1 / m ∗ d Z 2 ∗ A 1. T dW2=1/m*dZ2*A1.T dW2=1/m∗dZ2∗A1.T
d b 2 = 1 / m ∗ ∑ i = 0 m d Z 2 db2=1/m*\sum_{i=0}^mdZ2 db2=1/m∗i=0∑mdZ2
第一层的参数同理,这里要记住计算各参数梯度,就是高数中的链式法则,这也就是为什么叫做向后传播,想要计算前一层的参数导数值就要先计算出后一层的梯度值
y = 2 ∗ x y=2*x y=2∗x
z = 3 ∗ y z=3*y z=3∗y
∂ z / ∂ x = ( ∂ z / ∂ y ) ∗ ( d y / d x ) ∂z/∂x=(∂z/∂y )*(dy/dx) ∂z/∂x=(∂z/∂y)∗(dy/dx)
记住这个一切都OK!!!
def backward(W1,b1,W2,b2,X,Y):
"""
功能:向后传播,计算各个层参数的梯度(偏导)
参数:
W1:隐藏层的权值参数
b1:隐藏层的偏置参数
W2:输出层的权值参数
b2:输出层的偏置参数
X:特征矩阵
Y:标签
返回:
grads:各参数的梯度值
"""
# 样本数
m=X.shape[1]
# 进行前向传播,获取各参数值
forward_params=forward(W1,b1,W2,b2,X,Y)
A1=forward_params['A1']
A2=forward_params['A2']
W1=forward_params['W1']
W2=forward_params['W2']
# 计算梯度
dZ2= A2 - Y
dW2 = (1 / m) * np.dot(dZ2, A1.T)
db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)
dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2))
dW1 = (1 / m) * np.dot(dZ1, X.T)
db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)
grads = {
"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2 }
return grads
✌ 定义整个传播过程
一个传播流程包括:
- 向前传播
- 计算损失函数
- 向后传播
3.1 计算梯度
3.2 更新参数
def propagate(W1,b1,W2,b2,X,Y):
"""
功能:传播运算,向前->损失->向后->
参数:
W1:隐藏层的权值参数
b1:隐藏层的偏置参数
W2:输出层的权值参数
b2:输出层的偏置参数
X:特征矩阵
Y:标签
返回:
grads,loss:各参数的梯度,损失值
"""
# 计算损失
loss=loss_fn(W1,b1,W2,b2,X,Y)
# 向后传播,计算梯度
grads=backward(W1,b1,W2,b2,X,Y)
return grads,loss
✌ 定义优化器函数
目标是通过最小化损失函数 J来学习 w 和 b 。对于参数 λ,更新规则是 W 1 = W 1 − λ ∗ d J / d W 1 W1=W1-λ*dJ/dW1 W1=W1−λ∗dJ/dW1 b 1 = b 1 − λ ∗ d J / d b 1 b1=b1-λ*dJ/db1 b1=b1−λ∗dJ/db1 W 2 = W 2 − λ ∗ d J / d W 2 W2=W2-λ*dJ/dW2 W2=W2−λ∗dJ/dW2 b 2 = b 2 − λ ∗ d J / d b 2 b2=b2-λ*dJ/db2 b2=b2−λ∗dJ/db2,其中 λ 是学习率。
num_iter代表梯度下降时的迭代次数,就是w的改变次数,求取损失函数的最小值,即全局最优解,这里可能会产生局部最优解,会影响模型结果,这里不与阐述,可以选择其他较好的优化器
大多数优化器都是基于梯度下降这种方法,只不过具体的数学计算有些不同
def optimizer(W1,b1,W2,b2,X,Y,num_iter,lr,print_loss=False):
"""
功能:优化函数,进行梯度下降,不断更新权重值,求取最优解
参数:
W1:隐藏层的权值参数
b1:隐藏层的偏置参数
W2:输出层的权值参数
b2:输出层的偏置参数
X:特征矩阵
Y:标签
num_iter:梯度下降时的迭代次数
lr:学习率 w=w-lr*dw
print_loss:是否每100次迭代打印一次缺失值
返回:
params:训练好后的w和b值
losses:各迭代次数下的损失值
"""
# 存储不同迭代次数下的loss值
losses=[]
# 开始迭代
for i in range(num_iter):
# 获取损失和梯度值
grads,loss=propagate(W1,b1,W2,b2,X,Y)
dW1=grads['dW1']
db1=grads['db1']
dW2=grads['dW2']
db2=grads['db2']
# 参数更新
W1=W1-lr*dW1
b1=b1-lr*db1
W2=W2-lr*dW2
b2=b2-lr*db2
if i%100==0:
losses.append(loss)
if print_loss and i%100==0:
print('迭代次数:%d,误差值:%f'%(i+1,loss))
params={
'W1':W1,
'b1':b1,
'W2':W2,
'b2':b2}
return params,losses
✌ 定义预测函数
上面optimizer函数会输出已经训练好的w、b参数,我们可以利用它们进行预测新的样本集
进行预测两个步骤:
- y = a = s i g m o i d ( w . T ∗ X + b ) y=a=sigmoid(w.T*X+b) y=a=sigmoid(w.T∗X+b)
- 利用概率将其转化为0-1类别
- 将结果存储到y_pred中
def predict(W1,b1,W2,b2,X,Y):
"""
功能:利用优化好的w和b值进行预测
参数:
W1:隐藏层的权值参数
b1:隐藏层的偏置参数
W2:输出层的权值参数
b2:输出层的偏置参数
X:特征矩阵
Y:标签
返回:
y_pred:预测值(1,样本数)维
"""
# 样本数
m=X.shape[1]
# 预测矩阵
y_pred=np.zeros((1,m))
# 一层激活
A1=np.tanh(np.dot(W1,X)+b1)
# 二层激活
A2=sigmoid(np.dot(W2,A1)+b2)
# 进行分类
for i in range(m):
y_pred[0,i]=1 if A2[0,i]>0.5 else 0
return y_pred
✌ 定义模型函数
我们已经将所需要的所有函数已经封装好了,现在需要一个训练函数调用它们,完成模型的训练,model的作用就是如此
def model(x_train,x_test,y_train,y_test,num_iter,lr,print_loss=False):
"""
功能:利用前面封装好的函数进行训练
参数:
x_train:训练数据(特征数,样本数)
x_test:初始化好的权重矩阵(特征数,样本数)
y_train:初始化好的权重矩阵(1,样本数)
y_test:初始化好的权重矩阵(1,样本数)
num_iter:梯度下降的迭代次数
lr:学习率
print_loss:是否每100次打印loss值
返回:
d:预测结果以w,b等数据
"""
# 获取各层的节点数
in_layer,hidden_layer,out_layer=layer_size(x_train,y_train)
# 初始化参数
init_params=init_w_b(in_layer,hidden_layer,out_layer)
W1=init_params['W1']
b1=init_params['b1']
W2=init_params['W2']
b2=init_params['b2']
# 梯度下降
params,losses=optimizer(W1,b1,W2,b2,x_train,y_train,num_iter,lr,print_loss)
W1=params['W1']
b1=params['b1']
W2=params['W2']
b2=params['b2']
# 预测训练集和测试集
y_pred_train=predict(W1,b1,W2,b2,x_train,y_train)
y_pred_test=predict(W1,b1,W2,b2,x_test,y_test)
print('训练集的准确性:%.3f'%((y_pred_train==y_train).sum()/y_train.shape[1]*100),'%')
print('测试集的准确性:%.3f'%((y_pred_test==y_test).sum()/y_test.shape[1]*100),'%')
d = {
"losses" : losses,
"y_pred_train" : y_pred_train,
"y_pred_test" : y_pred_test,
"W1" : W1,
"b1" : b1,
"W2":W2,
"b2":b2,
"learning_rate" :lr,
"num_iter" : num_iter }
return d
✌ 分割数据集
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(X.T,np.squeeze(Y),test_size=0.2,random_state=2021)
x_train=x_train.T
x_test=x_test.T
y_train=np.array([y_train])
y_test=np.array([y_test])
✌ 进行测试
我们将我们处理好的训练测试集传入,测试下模型的效果,并每迭代100次打印下损失函数的值,观察模型效果是否得到了优化
print("====================测试model====================")
d = model(x_train,x_test,y_train,y_test,3000,4.2,True)
查看输出结果:
====================测试model====================
迭代次数:1,误差值:0.915083
迭代次数:101,误差值:0.341307
迭代次数:201,误差值:0.314505
迭代次数:301,误差值:0.301869
迭代次数:401,误差值:0.293965
迭代次数:501,误差值:0.288318
迭代次数:601,误差值:0.283970
迭代次数:701,误差值:0.280468
迭代次数:801,误差值:0.277569
迭代次数:901,误差值:0.275129
迭代次数:1001,误差值:0.273056
迭代次数:1101,误差值:0.271282
迭代次数:1201,误差值:0.269751
迭代次数:1301,误差值:0.268418
迭代次数:1401,误差值:0.267231
迭代次数:1501,误差值:0.266127
迭代次数:1601,误差值:0.265013
迭代次数:1701,误差值:0.263849
迭代次数:1801,误差值:0.263058
迭代次数:1901,误差值:0.262612
迭代次数:2001,误差值:0.262124
迭代次数:2101,误差值:0.261580
迭代次数:2201,误差值:0.261060
迭代次数:2301,误差值:0.260638
迭代次数:2401,误差值:0.260392
迭代次数:2501,误差值:0.248556
迭代次数:2601,误差值:0.243686
迭代次数:2701,误差值:0.241531
迭代次数:2801,误差值:0.240559
迭代次数:2901,误差值:0.240050
训练集的准确性:90.000 %
测试集的准确性:91.250 %
✌ 测试简易神经网络(逻辑回归模型)
我们想要对比下加入了隐藏层和不加隐藏层的效果,我们需要建立一个不带隐藏层的神经网络,不过为了方便(懒得搭了),我们直接调用sklearn中的LogisticRegression库,其实是一样的,参数采取默认参数,如果参数调整一下,模型效果可能会更好
from sklearn.linear_model import LogisticRegression
clf=LogisticRegression()
score=cross_val_score(clf,X.T,np.squeeze(Y),cv=10)
for i,val in enumerate(score):
print('第%d折:%.3f'%(i+1,val))
print('Logistic模型平均效果:%.3f'%score.mean())
查看输出结果:
第1折:0.675
第2折:0.975
第3折:0.550
第4折:0.075
第5折:0.200
第6折:0.325
第7折:0.000
第8折:0.550
第9折:0.875
第10折:0.650
Logistic模型平均效果:0.487
✌ 测试LGB模型
import lightgbm as lgb
from sklearn.model_selection import cross_val_score
clf = lgb.LGBMClassifier(
boosting_type='gbdt', num_leaves=55, reg_alpha=0.0, reg_lambda=1,
max_depth=15, n_estimators=6000, objective='binary',
subsample=0.8, colsample_bytree=0.8, subsample_freq=1,
learning_rate=0.06, min_child_weight=1, random_state=20, n_jobs=4
)
score=cross_val_score(clf,X.T,np.squeeze(Y),cv=10)
for i,val in enumerate(score):
print('第%d折:%.3f'%(i+1,val))
print('LGB模型平均效果:%.3f'%score.mean())
查看输出结果:
第1折:0.425
第2折:0.850
第3折:0.825
第4折:0.900
第5折:0.925
第6折:0.975
第7折:0.875
第8折:0.700
第9折:0.775
第10折:0.525
LGB模型平均效果:0.778