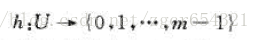前面讨论的各种数据结构中，记录在各种结构中的相对位置是随机的，和在记录的关键字之间不存在有确定的关系，因此在查找记录是需要进行一系列和关键字的比较。而理想的情况是不希望进行任何的比较，一次存取便能得到所查记录。那就必须在记录的存储位置和它的关键字之间建立一种确定的关系f，使每个关键字和结构中有一个唯一的存储位置与之相对应。我们称这个对应关系f为哈希函数，而按这个思想建立的表为哈希表。

在很多应用中，都要用到一种动态集合结构，它仅支持INSERT, SEARCH和DELETE字典操作。

实现字典的一种有效数据结构为散列表(hash table) 。在最坏情况下，在散列表中，查找一个元素的时间与在链表中查找一个元素的时间相同，在最坏情况下都是Θ(n)。但在实践中，散列技术的效率是很高的。

直接寻址表：

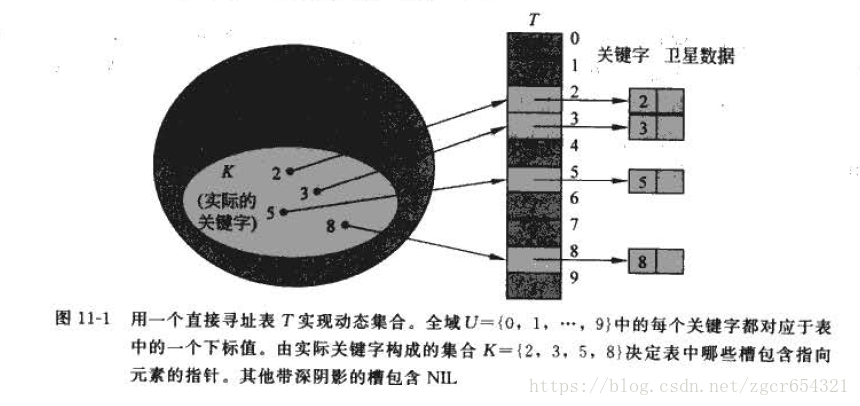
直接寻址表就是数组。当关键字的全域U比较小时，直接寻址是一种简单而有效的技术。如，如果全域为U={0，1，…,m-1}。则可以使用长度为m的数组。

如：

散列表：

直接寻址技术的缺点很明显：如果全域U很大，则存储大小为|U|的数组是不切实际的，而且如果实际存储的关键字集合K相对于全域U来说很小的时候，会造成巨大的浪费。此时采用散列表。

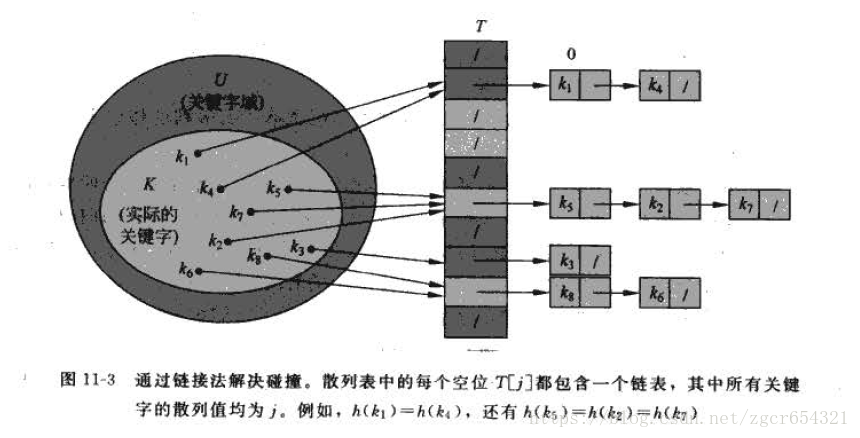
在直接寻址方式下，具有关键字k 的元素被存放在槽k中。在散列方式下，该元素处于h(k)中，即利用散列函数h, 根据关键字k计算出槽的位置。函数h将关键字域U 映射到散列表T[0...m-1]的槽位上：

采用散列函数的目的就在于缩小需要处理的下标范围，即我们要处理的值就从IUI降到m了，从而相应地降低了空间开销。

如：

这里会存在所谓“冲突”的问题：两个关键字可能被映射到同一个槽位中。由于全域|U|>M，所以冲突是无法避免的，所以一方面需要精心设计散列函数来尽量减少冲突的次数，另一方面是需要解决冲突的方法。

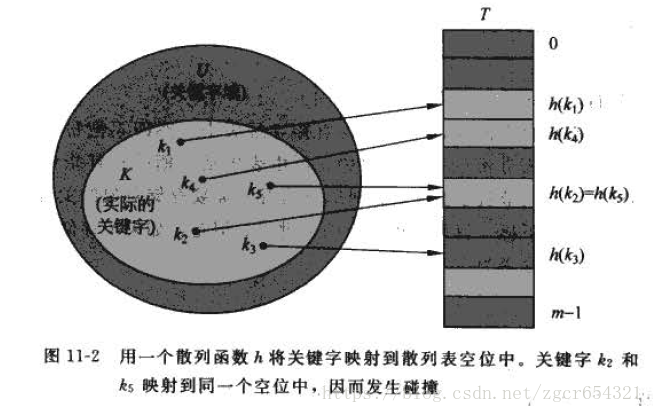
通过链接法解决碰撞：

在链接法中，把散列到同一槽中的所有元素都放在一个链表中，如下图所示。槽j中有一个指针， 它指向由所有散列到j的元素构成的链表的头；如果不存在这样的元素，则j中为NIL。

在采用链接法解决碰撞后，散列表T上的字典操作就很容易实现。

伪代码：

CHAINED-HASH-INSERT(T,x)
    insert x at the head of list T[h(key[x])]
CHAINED-HASH-SEARCH(T,k)
    search for an element with key k in list T[h(k)]
CHAINED-HASH-DELETE(T,x)
    delete x from the list T[h(key[x])]

插入操作的最坏情况运行时间为O(1) 。插入过程要快一些，因为假设要插入的元素x没有出现在表中；如果需要，在插入前执行搜索，可以检查这个假设（付出额外代价） 。查找操作的最坏情况运行时间与表的长度成正比。

对用链接法散列的分析：

给定一个具有m个槽位，存储了n个元素的散列表T，定义T的装载因子α为n/m，即，一个链表中的平均元素数目。α可能小于，等于，或大于1。

散列方法的平均性能依赖于所选取的散列函数h，将所有的关键字集合分布到m个槽位上的均匀程度。假定对于任何一个给定的元素，等可能的散列到m个槽位中的任何一个，且与其他元素被散列到什么位置上无关，称这个假设为简单均匀散列。

在简单均匀散列的情况下，对于采用链接法的散列表，一次不成功查找和一次成功查找所需的平均时间都为Θ(1+α)。

因此，若散列表的槽位数正比于其中的元素个数，我们有n = O(m)，于是，α = n/m = O(m)/m = O(1)。因此，查找时间平均为常数。由于插入操作首先需要调用CHAINED-HASH-SEARCH确认元素x的关键值未曾出现在表中，然后用O(1)时间将x插入到链表T[h(key[x])]中，所以期望的时间是O(1)。相仿地，删除操作对双向拉链表平均情形时间也是O(1)，所以所有的字典操作可以在O(1)的平均时间内得到支持。

散列函数：

 一个好的散列函数应（近似的）满足简单均匀散列假设：每个关键字都等可能的被散列到m个槽位中的任何一个，并与其它关键字已散列到哪个槽位无关。遗憾的是一般无法检查这一条件是否成立，因为很少能知道关键字的概率分布，而且各个关键字可能不是完全独立的。

如果知道关键字的概率分布，比如关键字都是随机的k，它们独立均匀分布在区间[0…1]中，那么散列函数h(k) = km就能满足简单均匀散列的条件。

将关键字解释为自然数：

多数散列函数都假定关键字域为自然数集N={0, 1, 2,··· } 。如果所给关键字不是自然数，则必须有一种方法来将它们解释为自然数。例如， 一个字符串关键字可以被解释为按适当的基数记号表示的整数。

除法散列法：

h(k) = k mod m

其中m为散列表的槽位数，使用除数散列法的时候，对于m的选择要慎重。比如m不应该是2的幂。否则如果m=2的p次方，则h(k)就是k的p个最低位数字（二进制）。除非已经知道关键字的最低p位数的排列是等可能的，否则在设计散列函数时，应该考虑关键字的所有位。

一个不太接近2的整数幂的素数是m个一个比较好的选择。

乘法散列法：

h(k) = m(kA mod 1)，其中"kA mod 1" 即kA的小数部分。

乘法方法的一个优点是对m的选择没有什么特别的要求， 一般选择它为2的某个幂次(m =2的p次方, p为某个整数)，最佳的选择为A。

直接定址法：

h(k) = k或 h(k) = ak + b 

其中a和b为常数。实际中能使用这种哈希函数的情况很少。

数字分析法：

假设关键字是以r为基的数（比如以10为基的十进制数），并且哈希表中可能出现的关键字都是事先知道的，则可取关键字的若干位组成哈希地址。

全域散列法：

全域散列的基本思想是在执行开始时，就从一族仔细设计的函数中、随机地选择一个作为散列函数。就像在快速排序中一样，随机化保证了没有哪一种输人会始终导致最坏情况性态。同时，随机化使得即使是对同一个输入，算法在每一次执行时的性态也都不一样。这样就可以确保对于任何输人，算法都具有较好的平均情况性态。

开放寻址法：

在开放寻址法(open addressing) 中，所有的元素都存放在散列表里。即每个表项或包含动态集合的一个元素，或包含NIL。当查找一个元素时，要检查所有的表项，直到找到所需的元素，或者最终发现该元素不在表中。

在开放寻址法中，散列表有可能会被填满，因而装载因子α <=  1。

在开放寻址法中，字典操作需要找到一个”槽序列”，比如要插入元素，需要按照某个槽序列探查散列表，直到找到一个空槽。探查的序列不一定是0,1…m-1。而是要依赖于待插入的关键字。对于每一个关键字k，探查序列为：h(k,i)   (0 <= i <= m-1)。

伪代码：

HASH_INSERT(T, k)            
    i= 0                      
    repeat j = h(k, i)                                     
        if T[j] == NIL
            then T[j]= k           
            return  j            
        else i=i+1               
    until  i==m
error  "hash table overflow"
HASH_SERACH(T,k)
    i = 0
    repeat j = h(k, i)
        if T[j] == k
            then return j
        i = i+1
        until T[j] == NIL or i ==m
    return NIL

查找关键字k的算法的探查序列与将k插入时的插入算法是一样的。当在查找过程中碰到一个空槽时，查找算法就（非成功地）停止，因为如果k确实在表中的话，也应该在该处，而不是探查序列的稍后位置上（之所以这样说，是因为我们假定了关键字不会被删除）。过程HASH-SEARCH的输入为一个散列表T和一个关键字k，如果槽j中包含关键字k则返回j；如果k不在表T中，则返回NIL 。

删除操作执行起来比较困难，当我们从槽i中删除关键字时，不能简单地让T[i]=NIL，因为这样会破坏查找的过程。假设关键字k在i之后插入到散列表中，如果T[i]被设为NIL，那么查找过程就再也找不到k了。解决这个问题的方法是引入一个新的状态DELETED，而不是NIL，这样在插入过程中，一旦发现DELETED的槽，便可以在该槽中放置数据，而查找过程不需要任何改动。但如此一来，查找时间就不再依赖于装载因子了，所以在必须删除关键字的应用中，往往采用链接法来解决碰撞。

均匀散列：

假设每个关键字的探查序列等可能的为（0,1,……m-1）的m!种排列中的任何一种。真正的均匀散列难以实现，有三种技术常用来计算开放寻址法中的探查序列：线性探查，二次探查，双重探查。这些技术均不满足均匀散列的假设。

线性探查：

h(k,i) = (h’(k) + i) mod m    i = 0,1,…,m-1

给定一个关键字k，首先探查槽位h’(k)，然后是h’(k) + 1，以此类推，直到最后的h’(k)-1。在线性探查中，初始探查位置决定了整个序列，所以有m种不同的探查序列。

线性探查有个缺点，就是一次群集。当表中i，i+1，i+2位置上都已经填满时，下一个哈希地址为i，i+1，i+2，i+3的关键字记录都将竞争i+3的位置。随着连续被占用的槽位不断增加，平均查找时间也不断增加。

二次探查：

h(k,i) = (h'(k) + c1i +c2i^2) mod m     i = 0,1,…,m-1

后续的探查位置要在此基础上加上一个偏移量，该偏移量以二次的方式依赖于探查号i。这种探查的效果要比线性探查好。但是，如果两个关键字的初始探查位置相同，那它们的探查序列也是相同的，这一性质会导致二次群集。类似于线性探查，二次探查也仅有m个不同的探查序列。

双重散列：

h(k,i) = (h1(k) +i*h2(k)) mod m     i = 0,1,…,m-1

其中h1和h2为辅助散列函数。初始探查位置为T(h1(k) ] , 后续的探查位置在此基础上加上偏移量h2(k)模m 。

双重散列是开放寻址法中的最好方法之一，不像线性和二次探查，双重探查的的探查序列以两种不同的方式依赖于关键字k。

为能查找整个散列表，值h2(k)要与表的大小m互质。确保这个条件成立的一种方法是取m为2的幕，并设计一个总产生奇数的h2。另一种方法是取m为质数，并设计一个总是产生较m小的正整数的h2。

如：

我们可以取m为质数，并取h1(k) = k mod m, h2(k) = 1 + (k mod m')，其中m' 略小于m( 如m-1) 。比如，如果k=123456 ，m=701， m'=700，则有h1(k)=80，h2(k) = 257, 可知第一个探查位置为80, 然后检查每第257个槽（模m), 直到找到该关键字，或查过了所有的槽。

给定一个装载因子为a=n/m< l 的开放寻址散列表，在一次不成功的查找中，期望的探查数至多为1/ (1 一a) 。假设散列是一致的。

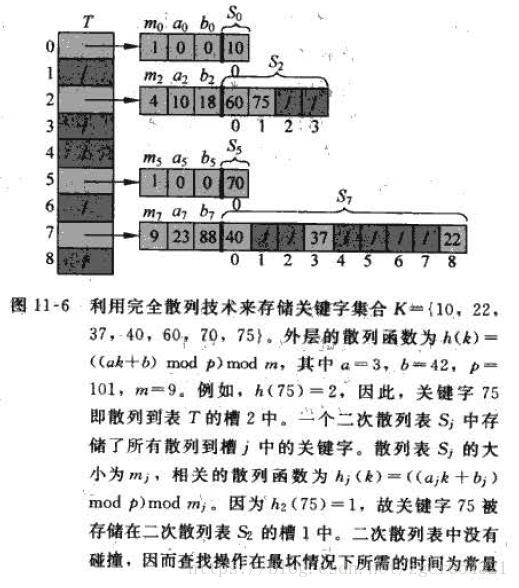
完全散列：

完全散列将关键字通过一级散列函数h1和二级散列函数h2后映射到二级散列中，其中，关键字个数等于桶数(n=m)，二级散列的大小N(T[i])为关键字个数的平方，用以保证完全O(n)的存储空间，以及O(1)的访问效率。但实际上，不可能真正地完全实现无冲突。

如：