GRU-ODE-Bayes论文翻译

1 Introduction

本文提出（1）门控循环单元的连续时间版本，以及（2）处理零星观测的贝叶斯更新网络。我们将这两个想法结合起来，形成了GRU-ODE-Bayes方法。

在2D Ornstein-Uhlenbeck过程和高度相关的Wiener过程

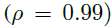上比较GRU-ODE-Bayes和NeuralODE-VAE。 点是从中获得零星观测值的实际基础过程（虚线）的值。实线和阴影区域是推断的平均值和95％的置信区间。请注意， GRU-ODE-Bayes与NeuralODE-VAE的误差较小且方差较小。 还要注意， GRU-ODE-Bayes可以推断出一个变量的跳跃也意味着另一个未观察到的变量（红色箭头）的跳跃。同样， 它也学习了由于新的输入观测值而导致的方差的减少

如图1所示，GRU-ODE-Bayes可以（1）快速推断潜在随机过程的未知参数，并且（2）了解其变量之间的相关性（图1中的红色箭头）。相反，Chen等人提出的基于编码器-解码器的方法NeuralODE-VAE。（2018）捕获了流程的一般结构，但无法恢复变量之间的详细交互（详细比较请参见第4节）。

我们假设观测值yi是从D维随机过程Y（t）的实现中采样的，该过程的动力学是由未知SDE驱动的：

Wiener Process 是随机过程的一种，而且是非常重要的一种，也称为布朗运动或（标准）布朗运动过程。

dW(t)是 维纳过程。 Y(t)的分布然后根据著名的福克 - 普朗克方程进行演化。我们将其概率密度函数（PDF）的均值和协方差参数称为

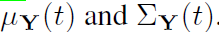
我们的目标是根据零星的测量值yi来模拟未知的时间函数

。这些是通过在时间ti对随机向量Y(t)采样并带有一些观察噪声而获得的。并非每次都采样所有维度，导致yi值缺失。与经典的SDE推论相反，我们认为函数

是由神经网络参数化的。

2 Proposed method

在较高的层次上，我们提出了一种双模系统，该双模系统由

（1）受GRU启发的连续时间状态演化 ( GRU-ODE)，它在观察之间及时传播系统的隐藏状态h。

（2）更新当前隐藏状态以合并传入的观测值 (GRU-Bayes)。每当有新的观测值可用时，系统就会从传播切换到更新，然后再切换回来。

2.1 GRU-ODE derivation

为了得出基于GRU的ODE，我们首先证明Cho等人提出（2014）的GRU.

首先，令

为GRU的重置门，更新门和更新向量：

都是[0,1]的范围

其中

为元素乘积。然后，GRU的隐藏状态h的标准更新为

我们也可以写成

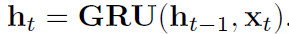。通过从该状态更新方程式中减去

并分解出（

），我们得到一个差分方程式

这个差分方程自然会导致h(t)的以下ODE：

2.2 General properties of GRU-ODE

GRU-ODE几个有用的性质：

有界：首先，隐藏状态h（t）保持在[-1，1]范围内。此限制对于与GRU-Bayes模型的兼容性至关重要，它来自公式 3中的负反馈项，可以稳定生成的系统。详细地说，如果起始状态h（0）的第j维在[-1，1]之内，则h（t）j将始终保持在[-1，1]之内，因为：

转存失败重新上传取消

连续性：其次，GRU-ODE是具有常数K = 2的 Lipschitz连续。重要的是，这意味着GRU-ODE编码了潜在过程h（t）之前的连续性。这符合产生观察结果的连续隐藏过程的假设（等式1）。

Lipschitz连续： 一个连续函数

上面额外施加了一个限制，要求存在一个常数

使得定义域内的任意两个元素

都满足：

此时称函数

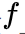的Lipschitz常数为K

一般数值积分： 作为参数化的 ODE ， GRU-ODE 可以与任何数值求解器集成。特别地，可以使用 自适应步长求解器 。然后，我们的模型可以利用内部方程 3 的连续时间公式，在内部动力学较慢时提供较大的时间步长。还可以通过复杂的 ODE 集成方法使其更快。我们实现了以下方法： Euler ，显式中点和 Dormand-Prince （自适应步长方法）。

2.3 GRU-Bayes

GRU-Bayes是处理偶发进入的观测值以更新隐藏矢量，从而更新Y(t)的估计PDF(概率密度函数)的模块。该模块基于标准GRU，因此在GRU-ODE所需的[-1,1]区域中操作。特别是,GRU-Bayes 能够将h(t)更新到该区域中的任何点。只需一次观察，任何调整都将触手可及。

要为GRU-Bayes内部的GRU单元提供一个无法完全观测的向量，我们首先使用fprep用mask对它进行预处理，如附录D所述。对于给定的时间序列，在时间t = t [k]时使用掩码m [k]和隐藏向量h（t_）的第k个观测值y [k]的结果更新为

其中h（t_）和h（t +）表示从GRU-Bayes更新跳转之前和之后的隐藏表示。

2.4 GRU-ODE-Bayes

提出的GRU-ODE-Bayes结合了GRU-ODE和GRU-Bayes。 GRU-ODE用于在观察之间的连续时间内演化隐藏状态h（t），而GRU-Bayes基于观察y将隐藏状态从h（t_）转换为h（t +）。如图2最佳所示，GRU-ODE和GRU-Bayes之间的交替会导致ODE发生跳跃，其中跳跃位于观测点的位置。

最好将GRU-ODE-Bayes理解为一种过滤方法。根据以前的观察（直到时间t[k]），它可以估计将来观察的概率。像著名的卡尔曼滤波器一样，它在预测（GRU-ODE）和滤波（GRU-Bayes）阶段之间交替。通过在时间上集成隐藏过程h（t）来预测时间序列的未来值，如图2中的绿色实线所示。当有新的测量可用时，更新步骤将离散地更新隐藏状态（蓝色虚线）。请注意，与卡尔曼滤波器不同，我们的方法能够为隐藏过程学习复杂的动力学。

Objective function

第一个损失

是在 观测值更新之前计算的，它是观测值的负对数似然（NegLL）。为了观察单个样本，我们有（出于可读性考虑，我们删除了时间索引）：

其中，

是观测掩码，而

是更新前维度j的分布参数。因此，仅根据观察到的y值计算误差。

第二个损失，让

表示GRU-Bayes之前的预测分布（来自h_）

对于

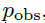，给出噪声观察（带有噪声矢量）的Y（t）的PDF(概率密度函数)，我们首先计算贝叶斯更新的类似物

让

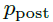表示应用GRU-Bayes后的预测分布（来自h +）。然后，将跳后损失定义为

之间的KL散度：

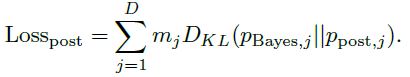
通过这种方式，我们强迫我们的模型学习模仿贝叶斯更新。

与跳跃前的损失类似，仅针对观察到的尺寸计算损失后。然后，通过将两个损失与加权参数lambda相加来获得总损失

算法1中描述了GRU-ODE-Bayes的伪代码，其中显示了单个时间序列的前向通过。

为了对多个时间序列进行小批量处理，我们 对所有时间序列的观测时间进行排序，并针对每个唯一时间点t [k]， 创建一个具有观测值的时间序列的列表。算法的主循环遍历这组独特的时间点。在GRU-ODE步骤中，我们共同传播所有隐藏状态。 GRU-Bayes更新和损失计算仅在该特定时间点具有观察力的时间序列上执行。然后， 我们的方法的复杂性随观察次数成线性比例，随观察维度成二次比例。

当内存成本成为瓶颈时，可以使用 伴随方法计算梯度，而无需通过求解器操作进行反向传播

对于二项分布和高斯分布，可以通过分析来计算Losspost。在高斯分布的情况下，我们可以计算贝叶斯更新的均值

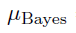和方差

：

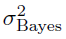4 Application to synthetic SDEs

图1展示了我们的方法与NeuralODE-VAE相比，在由带有随机参数的多变量Ornstein-Uhlenbeck（OU）SDE驱动的过程中生成的数据上的能力。与检索样本平均动态的NeuralODE-VAE相比，我们的方法可以检测两个特征之间的相关性，并在进行新观察时更精确地更新其预测到达。特别要注意的是，即使仅观察到另一特征，GRU-ODE-Bayes也会利用其相关性这一事实来更新其对特征的预测和置信度。这可以在图1的左窗格中看到，其中在时间t = 3时，由于观察到了维度2（绿色），因此维度1（蓝色）已更新。

通过将零星输入直接输入到ODE中，GRU-ODE-Bayes依次过滤隐藏状态，从而估计未来观测值的PDF。这是所提出方法的核心优势，使其能够进行长期预测

在附录I中，我们进一步表明，我们的模型可以准确地表示带有随机变量的多变量OU过程的动力学。我们的模型还可以处理非线性SDE，如附录J所示，在这里，我们举了一个实例，该实例受Brusselator（Prigogine，1982年）的启发，是一种混沌的ODE。

5 Empirical evaluation

我们根据来自不同应用领域的两个数据集评估了我们的模型：医疗保健和气候预测。在这两种应用中，我们都假设数据由来自底层的嘈杂观测组成。如方程式中未观察到的潜在过程。 1.我们专注于预测未来时间点的时间序列的一般任务。对模型进行训练以最大程度地减少负面对数可能性。

5.1 Baselines

NeuralODE-VAE：我们将隐藏表示的时间导数建模为2层MLP。为了考虑到要素之间的缺失，我们添加了一种机制来提供观察蒙版

Imputation Methods：我们实现了两种插补方法，如Che等人所述。（2018）：GRU-Simple和GRU-D。

Sequential VAEs ：我们通过提供观察掩模并相应地更新损耗函数，扩展了深度卡尔曼滤波器的结构。

T-LSTM：我们重用了建议的时间感知LSTM单元，以设计带有观测蒙版的预测RNN。

5.2 Electronic health records

电子病历（EHR）分析对于实现数据驱动的个性化医学至关重要（Lee等人，2017; Goldstein等人，2017; Esteva等人，2019）。但是，对这种类型的数据进行有效建模仍然具有挑战性。确实，它由零星观察到的纵向数据组成，并具有额外的障碍，即没有标准的方法可以对齐患者的轨迹（例如，在入院时，患者的病情进展可能会非常不同）。这些困难使EHR分析非常适合GRU-ODE-Bayes。我们使用可公开获得的MIMIC-III临床数据库（Johnson等，2016），其中包含针对60,000多名重症监护患者的EHR。我们选择了具有充分观察力的21,250名患者的子集，并在患者入院后48小时内提取了96种不同的纵向实值测量值。我们将向读者介绍附录K，以获取有关队列选择的更多详细信息。我们专注于在36小时的观察窗口之后的下3次测量的预测。

5.3 Climate forecast

从短期天气预报到长期预测或评估系统变化，例如全球变暖，气候数据一直是时间序列分析的流行应用。通常认为此数据是在很长一段时间内定期采样的，这有助于对其进行统计分析。但是，这种假设通常在实践中不成立。数据丢失是气候研究中经常遇到的一个问题，其原因之一是测量错误，传感器故障或数据采集错误。然后，实际数据是零星的，研究人员通常在统计分析之前求助于插补（Junninen等，2004； Schneider，2001）。我们使用公开可用的美国历史气候学网络（USHCN）每日数据集（Menne等人），该数据集包含150年来5个气候变量（每日温度，降水和降雪）的测量值，这些数据分布在美国各地的1,218个气象站状态。我们选择了1114个站的子集，并选择了4年（1996年至2000年）的观测窗口。为了使时间序列零星分布，我们对数据进行二次采样，以使每个站在这4年中的平均观测值约为60。附录L包含有关此过程的其他详细信息。然后的任务是在观察的前3年中预测接下来的3次测量。

5.4 Results

我们使用5倍交叉验证报告性能。使用内部保留验证集（20％）选择超参数（丢失和权重衰减）

在一个遗漏的测试集（10％）上评估性能。为了重现性和公平比较，这些折痕可重新用于我们评估的每个模型（更多详细信息，请参见附录O）。表1中报告了这两个任务（NegLL和MSE）的性能指标。GRU-ODE-Bayes更自然地处理了零星数据，并且可以更精细地对观察到的特征之间的动力学和相关性进行建模，与其他方法相比，其性能更高。两个数据集。特别是，GRU-ODE-Bayes在这两个数据集上的性能均优于其他所有方法。

5.5 Impact of continuity prior

为了说明第2.1节中介绍的派生GRU-ODE单元的功能，我们考虑了使用小样本量进行时间序列预测的情况。在EHR预测领域中，这可以被构造为一种罕见的疾病设置，其中仅可用于少数患者的数据。在样品数量稀少的情况下，嵌入到GRU-ODE中的连续性至关重要，因为它提供了有关基础过程的重要先验信息。

为了强调GRU-ODE电池的重要性，我们比较了模型的两个版本：经典GRU-ODE-Bayes和一个版本，其中GRU-ODE电池被离散的自主GRU代替。我们称后者为GRU-Discretized-贝叶斯。表2显示了MIMIC-III在训练集中患者人数不同的结果。虽然我们的离散版本与完整数据集上的连续版本相匹配，但当样本数量较少时，GRU-ODE像元可实现更高的准确性，从而强调了连续性的重要性。对数似然结果在附录M中给出。

转存失败重新上传取消

小样本方案（MSE）中GRU-ODE与离散版本之间的比较。

附录A: GRU-ODE单元的完整公式：

其中：

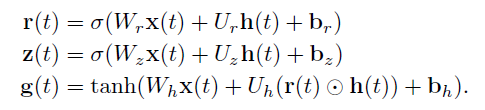
矩阵

和偏差向量为

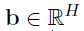是单元的参数，D是隐藏过程和输入的维数。

附录B： GRU-ODE Lipschitz连续

由于h在t上是可微的和连续的，我们从中值定理知道，对于任何

，存在这样的

取前面表达式的欧几里德范数，我们发现

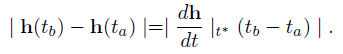
此外，我们还证明了h是在【-1，1】上有界的。因此，由于ODE中出现了有界函数（sigmoids和双曲正切），h的导数本身就有界于[-2，2]。我们的结论是h（t）是Lipschitz连续的，常数K=2。

附录C:数值积分方法的比较

我们实现了三种数值积分方法，其中包括经典的Euler方法和Dormand-Prince方法（DOPRI）。 DOPRI是一种流行的自适应步长数值积分，该方法依赖于2个阶数为4和5的Runge-Kutta求解器。自适应步长方法的优势在于，它们可以自动调整步数以将ODE积分到所需的点。

图3说明了在给定相同数据和相同ODE的情况下两个求解器采取的步骤数。我们观察到，使用自适应步长会导致一半的时间步长。更多步骤是如在图的右侧观察到的那样，在观察值附近获取并且随着基本过程变得更平滑，步长增大。但是，每个时间步骤所需的时间大大减少Euler的计算量要比DOPRI的计算量大，因此Euler的方法在我们到目前为止考虑的数据和模拟中显得更具竞争力。尽管如此，DOPRI仍可能是首选默认方法，因为它具有更好的数值稳定性

附录D 映射以处理跨要素缺失

GRU-Bayes的预处理步骤fprep处于隐藏状态h，并计算观测值

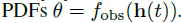的参数。在高斯的情况下，

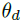包含Y（t）维d的均值和对数方差。然后，我们创建一个向量qd，该向量将

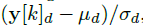与观测值y [k] d和归一化误差项连接起来，对于高斯情况为

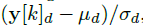，其中

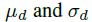是从d得出的平均值和标准偏差。然后，我们将向量qd与特定于维度的权重矩阵Wd相乘，并应用ReLU非线性。接下来，我们将所有没有观测值的结果归零（通过将它们乘以蒙版md）。最后，将结果的级联输入到GRU-Bayes的GRU单元中

附录E 观察模型映射

从隐藏的h到分布

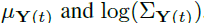的参数的映射。为此，我们使用具有25维隐藏层的经典多层感知器体系结构。请注意，我映射到方差的对数以保持正值。

附录F GRU-ODE-Bayes-seq

除了本文主要内容中描述的体系结构之外，我们还提出了一个变体，该变体可以顺序处理零星的输入。换句话说，GRU-Bayes将在隐藏的h上更新对一个输入维的预测，而不是对另一个输入维进行更新。我们称这种方法为GRU-ODE-Bayes-seq。

在针对GRU-Bayes的这种顺序方法中，我们首先在每个时间点应用预处理，然后将它们发送到GRU单元，从而对在时间t [k]观察到的所有y [k]维进行一对一处理。预处理步骤与非顺序方案中的步骤相同（附录D），但最后没有串联，因为一次只能处理一个维。请注意，尺寸的预处理无法并行完成，因为在处理每个尺寸后，隐藏状态h会发生变化，这会影响计算的

并因此影响所得的矢量qd。

附录G Minimal GRU-ODE

遵循与完整GRU单元相同的推理，我们还基于最小GRU单元得出了最小GRU-ODE单元。最小的GRU写道

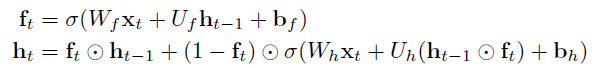
以上式子可以重写为微分方程：

则有ODE

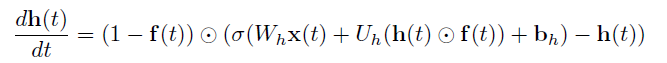
附录H GRU-Bayes的消融研究。

为了演示GRU-Bayes模块对我们的体系结构的适用性，我们进行了一项消融研究，在该消融研究中，我们用2层多层感知器代替了GRU-Bayes。我们对隐藏单元使用了tanh激活函数，对输出层使用了线性激活。我们在MIMIC数据集上针对预测任务评估了此修改后的体系结构的性能。结果显示在表3中。由于第2.2节和第2.3节中所述的特性，建议的体系结构优于简单的MLP模块。

附录I 在Ornstein-Uhlenbeck SDE中的应用

我们如Eq1所示，证明了我们的方法对由SDE驱动的流程生成的数据的功能。特别是，我们专注于多维相关的Ornstein-Uhlenbeck的扩展（OU）具有不同参数的过程。对于一个特定的样本i，动力学由遵循SDE：

其中W（t）是D维相关的维纳过程，ri是目标矢量，

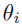是回复强度常数。为简单起见，我们将

参数视为标量。然后，通过实现具有样品特定参数的过程（5）来获得每个样品yi。

I.1 Representation capabilities

现在，我们证明我们的模型准确地捕获了方程5中定义的Y（t）分布的动力学。扩散过程的PDF演化由相应的Fokker-Planck方程给出。对于OU过程，该PDF是具有时间相关均值和协方差的高斯模型。基于在时间t的先前观察，得出

Y（t）的相关性是恒定的，并且等于Wiener过程的相关性。平均值和方差参数的动力学可以更好地表示为以下ODE形式：

初始条件为

接下来，我们研究如何用我们的GRU-ODE-Bayes表示此ODE的特定版本。

I.1.1 Standard Ornstein-Uhlenbeck process

当允许参数随样本变化时，这些参数必须以GRU-ODE-Bayes的隐藏状态编码，而不是以固定权重编码。对于

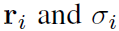，GRU-Bayes在观测值到达时计算并存储其当前估计值。这基于等式4中的先前隐藏和当前观察，然后，GRU-ODE模块只需在观察之间保持这些估计不变即可：

可以通过关闭更新门（即将这些维度的z（t）设置为1）轻松完成此操作，然后将这些隐藏状态用于输出等式6中的均值和方差。因此使模型能够代表与样本相关的

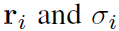的广义Ornstein-Uhlenbeck过程。

样本依赖的完美表示

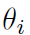需要将等式 6中的输入相乘。哪个GRU-ODE不能准确执行，但应该能够合理地近似。如果需要精确表示，则添加双线性层就足够了。

此外，当允许在同一样本中随时间改变参数时，同样的推理也适用。 GRU-Bayes再次能够使用新的估算值更新隐藏矢量

I.1.3 Non-aligned time series

我们的方法还可以处理将在时间上偏移的样本（即观察窗口未在固有时间尺度上对齐）。在第5节中介绍了在每个疾病的不同阶段记录的纵向患者数据的一个例子。该设置自然由GRU-Bayes模块处理。

I.2 Case Study: 2D Ornstein-Uhlenbeck Process

I.2.1设定

我们根据方程式中定义的相关布朗运动在二维OU过程中评估模型。 5.为了更好地说明其功能，我们考虑以下三种情况。在第一个设置中，ri随样本的不同而变化，分别为和

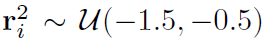。维纳过程之间的相关性设置为0.99。我们还设置

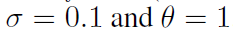1。第二种情况，我们称为随机滞后与第一种情况相似，但为每个样本添加了额外均匀分布的随机滞后。然后将样本时移某个

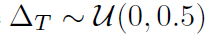。第三个设置与第一个设置相同，但值为0（即，两个维度都是独立的，并且它们之间没有共享信息）。

我们在时间t = 4之后评估样本预测的所有方法和设置。训练集包含10,000个样本，平均20个观察值分布在10秒的时间间隔内

图4：GRU-ODE-Bayes对带有未知参数的相关二维随机过程（虚线）的两个样本给出的预测示例（带阴影的置信区间）。点显示观察结果。该模型只需几个观察值即可推断出参数。此外，GRU-ODE-Bayes学习了尺寸之间的相关性，从而导致了未观察到的变量的更新（红色虚线箭头）。

使用负对数似然目标函数训练模型，但也报告了均方误差（MSE）。我们将我们的方法与NeuralODE-VAE进行了比较（Chen et al。，2018）。此外，我们考虑该模型的扩展版本，在该版本中还提供了称为NeuralODE-VAE-Mask的观察蒙版。

I.2.2 Empirical evaluation

图1显示了从随机ri设置发出的相同样本的NeuralODE-VAE和GRU-ODE-Bayes之间的预测比较。与检索样本平均动态的NeuralODE-VAE相比，我们的方法可以检测两个特征之间的相关性，并在观测值到达时更精确地更新其预测。特别要注意的是，即使仅观察到另一特征，GRU-ODE-Bayes也会利用其相关性这一事实来更新其对特征的预测和置信度。这可以在图1的左窗格中看到，其中在时间t = 3时，由于观察到了尺寸2（绿色），因此尺寸1（蓝色）已更新。

通过将零星输入直接输入到ODE中，GRU-ODE-Bayes依次过滤隐藏状态，从而估计未来观测值的PDF。这是所提出方法的核心优势，使其能够执行长期预测。相反，NeuralODE-VAE首先将整个动态存储在单个矢量中，然后将其映射到时间序列的动态（如图1所示）。

表4中显示的性能结果证实了这一分析。我们的方法在NegLL和MSE的所有设置上均表现更好。而且，该方法正确地处理了滞后（即第二种设置），因为它仅导致NegLL和MSE的边缘退化。当两个维度之间没有相关性（即

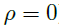）时，对一个维度的观察不包含关于另一个维度的信息，这会导致性能降低

图5说明了GRU-ODE-Bayes如何处理越来越多的观测结果，从而更新其预测和置信度。本示例适用于第一个设置（随机ri）。最初，预测具有较大的置信区间，并且反映了训练数据的一般统计数据。

然后，随着模型完善其对参数ri的预测，观测值逐渐减少了方差估计。随着更多数据的处理，预测收敛到基础过程的渐近分布。

图5：GRU-ODE-Bayes对随机ri设置的每次新观测都更新了其预测轨迹。阴影区域是根据先前的观察结果传播的置信区间。

J Application to synthetic nonlinear SDE: the Brusselator

除了扩展的多元OU过程之外，我们还研究了非线性SDE。我们从Ilya Prigogine提出的Brusselator ODE衍生出来，以模拟自动催化反应（Prigogine，1982年）。这是一个二维过程，其特征在于以下方程式：

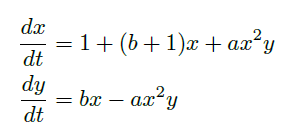
其中x和y代表过程的两个维度，而a和b是ODE的参数。当b> 1 + a时，该系统变得不稳定。我们在此过程中添加了一个随机组件，以使其成为以下SDE，我们将对其进行建模：

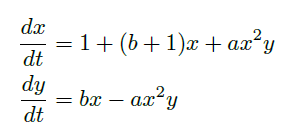
其中dW1（t）和dW2（t）是具有相关系数的相关布朗运动。我们模拟了由等式中给出的动力学驱动的1,000条轨迹。参数a = 0.3和b = 1.4的图7中所示，使得ODE不稳定。图6显示了此过程的一些实现。我们用于训练的数据集包含来自长度为50的那些轨迹的随机样本。我们以每10秒4个样本的平均速率进行零星采样。

图6：随机Brusselator Eq7在50秒内生成的轨迹示例。由于随机成分和对初始条件的敏感性，轨迹会有所不同。橙色和蓝色线代表该过程的两个组成部分。

图7显示了在所建议的随机Brusselator过程的不同样本（新生成的样本）上训练模型的预测。在每个时间点都会显示已过滤过程的平均值和标准偏差。我们强调，这意味着这些预测仅使用它们之前的观察结果。红色箭头表示在流程的两个维度之间共享信息。当仅观察到另一个维度时，该模型能够获取维度之间的相关性以更新其对一个维度的信念。这些图中显示的模型使用了带有DOPRI求解器的50维潜像。

图7：Brusselator的预测轨迹示例。该模型已使用DOPRI求解器进行了训练。实线表示预测的滤波平均值，阴影区域表示95％的置信区间，而虚线表示真实的生成过程。点显示可用于过滤的观察结果。红色箭头表示信念函数从一个维度到另一个维度的崩溃。

清风.伴酒.

发布了34 篇原创文章 · 获赞 3 · 访问量 741

私信关注

GRU-ODE-Bayes论文翻译

猜你喜欢