更多导数例子

在这个视频中我将给出一个更加复杂的例子，在这个例子中，函数在不同点处的斜率是不一样的，先来举个例子:

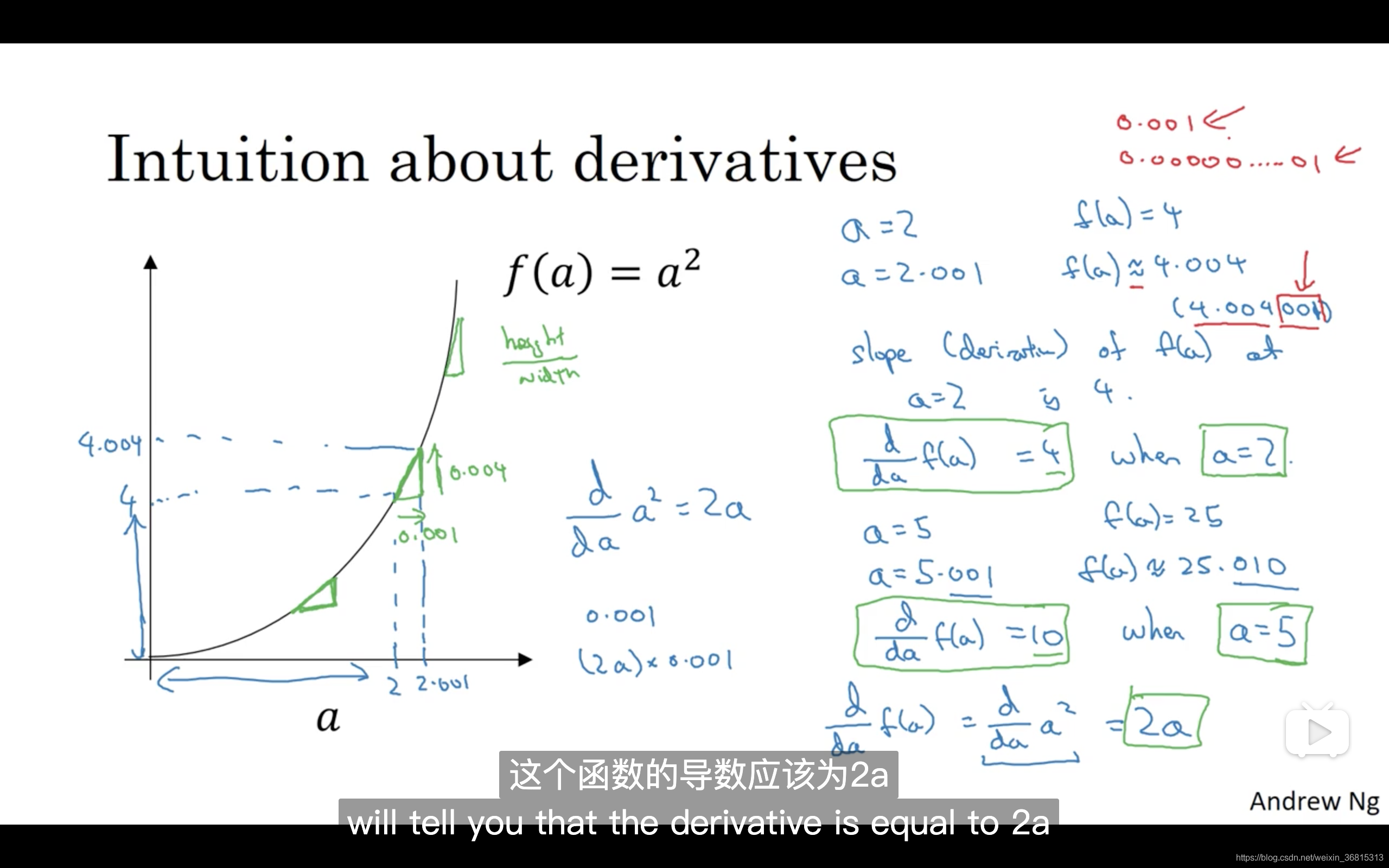
我在这里画一个函数， $f(a)=a^2$ ，如果 $a=2$ 的话，那么 $f(a)=4$ 。让我们稍稍往右推进一点点，现在 $a=2.001$ ，则 $f(a)\approx 4.004$ (如果你用计算器算的话，这个准确的值应该为4.004。0.001 我只是为了简便起见，省略了后面的部分)，如果你在这儿画，一个小三角形，你就会发现，如果把 $a$ 往右移动0.001，那么 $f(a)$ 将增大四倍，即增大0.004。在微积分中我们把这个三角形斜边的斜率，称为 $f(a)$ 在点 $a=2$ 处的导数(即为4)，或者写成微积分的形式，当 $a=2$ 的时候， $\frac{d}{da}f(a)=4$ 由此可知，函数 $f(a)=a^2$ ，在 $a$ 取不同值的时候，它的斜率是不同的，这和上个视频中的例子是不同的。

这里有种直观的方法可以解释，为什么一个点的斜率，在不同位置会不同如果你在曲线上，的不同位置画一些小小的三角形你就会发现，三角形高和宽的比值，在曲线上不同的地方，它们是不同的。所以当 $a=2$ 时，斜率为4；而当 $a=5$ 时，斜率为10 。如果你翻看微积分的课本，课本会告诉你，函数 $f(a)=a^2$ 的斜率（即导数）为 $2a$ 。这意味着任意给定一点 $a$ ，如果你稍微将 $a$ ，增大0.001，那么你会看到 $f(a)$ 将增大 $2a$ ，即增大的值为点在 $a$ 处斜率或导数，乘以你向右移动的距离。

现在有个小细节需要注意，导数增大的值，不是刚好等于导数公式算出来的值，而只是根据导数算出来的一个估计值。

为了总结这堂课所学的知识，我们再来看看几个例子：

假设 $f(a)=a^3$ 如果你翻看导数公式表，你会发现这个函数的导数，等于 $3a^2$ 。所以这是什么意思呢，同样地举一个例子：我们再次令 $a=2$ ，所以 $a^3=8$ ，如果我们又将 $a$ 增大一点点，你会发现 $f(a)\approx8.012$ ， 你可以自己检查一遍，如果我们取8.012，你会发现 $2.001^3$ ，和8.012很接近，事实上当 $a=2$ 时，导数值为 $3*2^2$ ，即 $3*4=12$ 。所以导数公式，表明如果你将 $a$ 向右移动0.001时， $f(a)$ 将会向右移动12倍，即0.012。

来看最后一个例子，假设 $f(a)=\log_e(a)$ ，有些可能会写作 $\ln(a)$ ，函数 $\log a$ 的斜率应该为 $\frac1a$ ，所以我们可以解释如下：如果 $a$ 取任何值，比如又取 $a=2$ ，然后又把 $a$ 向右边移动0.001 那么 $f(a)$ 将增大 $\frac1a*0.001$，如果你借助计算器的话，你会发现当 $a=2$ 时 $f(a)\approx0.69315$ ；而 $a=2.001$ 时， $f(a)\approx0.69365$ 。所以 $f(a)$ 增大了0.0005，如果你查看导数公式，当 $a=2$ 的时候，导数值 $\frac{d}{da}f(a)=\frac12$ 。这表明如果你把 $a$ 增大0.001，将只会 $f(a)$ 增大0.001的二分之一，即0.0005。如果你画个小三角形你就会发现，如果 $x$ 轴增加了0.001，那么 $y$ 轴上的 $\log a$ 函数，将增大0.001的一半 即0.0005。所以 $\frac1a$ ，当 $a=2$ 时这里是 ，就是当 $a=2$ 时这条线的斜率。这些就是有关导数的一些知识。

在这个视频中，你只需要记住两点：

第一点，导数就是斜率，而函数的斜率，在不同的点是不同的。在第一个例子中 $f(a)=3a$ ，这是一条直线，在任何点它的斜率都是相同的，均为3。但是对于函数 $f(a)=a^2$ ，或者 $f(a)=\log a$ ，它们的斜率是变化的，所以它们的导数或者斜率，在曲线上不同的点处是不同的。

第二点，如果你想知道一个函数的导数，你可参考你的微积分课本或者维基百科，然后你应该就能找到这些函数的导数公式。

最后我希望，你能通过我生动的讲解，掌握这些有关导数和斜率的知识，下一课我们将讲解计算图，以及如何用它来求更加复杂的函数的导数。

课程PPT