最近在练习最近公共祖先,写一篇博客记录一下
(注:博主一般不会在代码中写注释,如果不能理解的话就请换一个博客看吧)
前置芝士:树相关知识,倍增相关知识(博主不会写tarjan)
1.最近公共祖先指什么?
对于有根树T的两个结点u、v,最近公共祖先LCA(T,u,v)表示一个结点x,满足x是u和v的祖先且x的深度尽可能大。在这里,一个节点也可以是它自己的祖先
——摘自百度百科
2.求最近公共祖先的方法有什么?
- 向上标记法
- 倍增法
- tarjan
3.它们的适用情况?
向上标记法被另两个吊起来打,在线算法倍增法,离线算法tarjan
1.向上标记法
由于本算法在实际中使用较少,这里只是介绍一下它的主要思想
向上标记法的主要思想就是让两个节点同时向根移动并标记走过的路径
当一个节点走到了另一个节点走到过(有标记的节点)时,这个走到的节点就是他们的公共祖先(这个很好想,这里不多说了)
根据以上过程,我们可以得出向上标记法的查询复杂度为O(n),则总时间复杂度为O(n*q)(n为节点个数,q为询问个数)
再提一句:虽然看起来这个算法的时间复杂度很高,但是如果是随机数据,在平常情况下表现还是挺好的
2.倍增法
(敲黑板,重点来了)
先约定一下:lca(x,y)在本文中的意思为x,y的最近公共祖先
倍增法我个人理解就是对向上标记法的一种优化,两者思想差别不大
我们发现向上标记法的瓶颈在于它的向上跳的过程太慢了,我们试着用倍增法加速一下这个过程
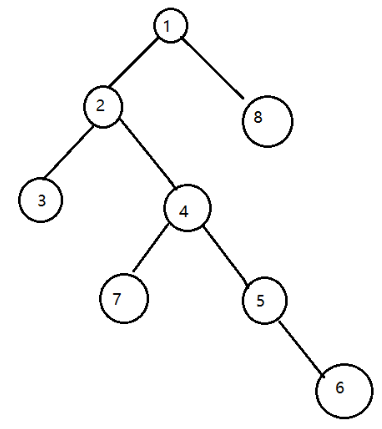
(先放个图)
(下面都是重点,课代表拿小本本记下来不好好听的人)
由于是倍增法,我们就可以先设计出两个数组:令f[i][j]表示第i个节点的2j祖先,d[i]表示i的深度
我在这里设x为深度较大的节点,y为深度较小的节点
我们可以先让深度最大的那个点x跳到 j 尽可能大的 2j 祖先且不能跳过y的深度,也就是跳到的深度大于等于y的深度
这一步的目的就是让x,y在同一深度,因为根据二进制拆分,x可以跳到它的任意一级祖先
然后我们判断一下此时是否x、y相重合,重合则说明x、y跳到的位置都是公共祖先,随意输出一个便可
若此时x,y没有重合,我们就让他们尝试着一起向上跳2j级祖先,但是不能让他们相遇——此时若是让他们相遇,不能保证一定是最近公共祖先
(这里请各位不理解的读者拿个本子写写画画,或者可以从网上找一些题目数据手动模拟一下,博主给出来的图比较弱)
然后我们怎么得到最近公共祖先呢?根据二进制拆分,每个数都能拆分成多个二进制数相加的形式,所以此时x、y必定只差一步就可以相会了,我们返回x的父节点(即f[x][0]即可)
下面我来举个栗子,帮助理解一下
我们看上面的那个图,如果我们要求lca(6,8),我们该怎么求?
这里我们先让6跳到符合条件的最远的2j节点,也就是节点2(先跳21到4,再跳20到2)
这里2和8并未重合,我们进行下一步,让他们同时向上跳
这里由于数据问题……并没有办法让他们向上跳
接下来我们讨论一下时间复杂度和其他东西
我们根据树的知识可以很容易得到我们把f数组的第二位设置成log(n)就行了。这个还是很好想的吧,因为你一共就要跳2j次
为了我们后面查询,我们是需要对f数组进行预处理的,这里用dfs或者bfs都行。
博主更推荐bfs一点,因为bfs在搜索完了之后不用再循环处理了
这里给出两者预处理的代码:
dfs版

const int N=100001; int f[N][31],d[N],root; inline void dfs(int x) { for(register int i=head[x];i;i=e[i].nxt) { register int y=e[i].ver; if(d[y]) continue; d[y]=d[x]+1; f[y][0]=x; dfs(y); } } inline void prework() { d[root]=1; dfs(root); for(register int i=1;i<=n;i++) { for(register int j=1;j<=t;j++) f[i][j]=f[f[i][j-1]][j-1]; } }
bfs版

const int N=100001; int f[N][31],d[N],root; queue<int> q; inline void bfs() { q.push(1); d[1]=1; while(q.size()) { register int x=q.front(); q.pop(); for(register int i=head[x];i;i=e[i].nxt) { register int y=e[i].ver; if(d[y]) continue; d[y]=d[x]+1; f[y][0]=x; q.push(y); for(register int j=1;j<=t;j++) f[y][j]=f[f[y][j-1]][j-1]; } } }
然后是查询的代码

inline int lca(int x,int y) { if(d[x]>d[y]) swap(x,y); for(register int i=t;i>=0;i--) if(d[f[y][i]]>=d[x]) y=f[y][i]; if(x==y) return x; for(register int i=t;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i]; return f[x][0]; }
要是你还没有理解(或者是想要代码)我在这里先讲几道题,难度由小到大(还有毒瘤题)
先放一道测试代码正确性用的洛谷模板题:P3379【模板】最近公共祖先(LCA)
下面开始讲解
1.#10130 「一本通 4.4 例 1」点的距离(简单题)
这道题其实是lca的基本运用,我们在代码中新加一个数组dis[i]表示i到根root路径上的边权和,在搜索的时候顺便维护一下即可,画个图就不难发现查询的时候答案为dis[x]+dis[y]-2*dis[lca(x,y)](这个是比较套路的)
喜闻乐见的,代码

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<queue> #include<cmath> using namespace std; const int N=100001; struct need{ int ver,nxt; }e[N<<1]; int n,m,t,head[N],tot,f[N][31],d[N]; queue<int> q; inline void add(int x,int y) { e[++tot].ver=y,e[tot].nxt=head[x],head[x]=tot; } inline void bfs() { q.push(1); d[1]=1; while(q.size()) { register int x=q.front(); q.pop(); for(register int i=head[x];i;i=e[i].nxt) { register int y=e[i].ver; if(d[y]) continue; d[y]=d[x]+1; f[y][0]=x; q.push(y); for(register int j=1;j<=t;j++) f[y][j]=f[f[y][j-1]][j-1]; } } } inline int lca(int x,int y) { if(d[x]>d[y]) swap(x,y); for(register int i=t;i>=0;i--) if(d[f[y][i]]>=d[x]) y=f[y][i]; if(x==y) return x; for(register int i=t;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i]; return f[x][0]; } inline int read() { register int x=0,m=1;register char ch=getchar(); while(ch<'0' || ch>'9'){if(ch=='-') m=-1;ch=getchar();} while(ch>='0' && ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();} return x*m; } int main() { n=read(); t=log(n)/log(2)+1; for(register int i=1;i<n;i++) { register int x=read(),y=read(); add(x,y),add(y,x); } bfs(); m=read(); for(register int i=1;i<=m;i++) { register int x=read(),y=read(),LCA=lca(x,y); printf("%d\n",d[x]+d[y]-d[LCA]*2); } return 0; }
2.#10131 「一本通 4.4 例 2」暗的连锁(中等难度吧)
这道题就用到了lca的一个基本运用:树上差分
我们先来分析一下这个题目,明显的,Dark的所有主要边为一棵树。当你要切断的树边在一个环中的时候,此时只有切断另一条环上的边,方案数+1,;当这个树边不在任何一个环中,你随便切都行,方案数+m;当这个树边在两个环中,那你不管怎么切,总是会有一个环,不统计答案
那么我们怎么判断环呢?树上差分就行了。我们先设每个点的权值为0,读入一条非树边的时候,这两个端点的权值加一,则这两个端点的lca减二。最后进行一次dfs求出当前节点在几个环中:0则不在环中,1在环中,2在两个环中
不太明白的可以看着代码理解一下

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<queue> #include<cmath> using namespace std; const int N=100001; struct need{ int ver,nxt; }e[N<<1]; int n,t,m,head[N],tot,d[N],f[N][31],tree[N],ans; queue<int> q; inline void add(int x,int y) { e[++tot].ver=y,e[tot].nxt=head[x],head[x]=tot; } inline void bfs() { q.push(1); d[1]=1; while(q.size()) { register int x=q.front(); q.pop(); for(register int i=head[x];i;i=e[i].nxt) { register int y=e[i].ver; if(d[y]) continue; d[y]=d[x]+1; f[y][0]=x; for(register int j=1;j<=t;j++) f[y][j]=f[f[y][j-1]][j-1]; q.push(y); } } } inline int lca(int x,int y) { if(d[x]>d[y]) swap(x,y); for(register int i=t;i>=0;i--) if(d[f[y][i]]>=d[x]) y=f[y][i]; if(x==y) return x; for(register int i=t;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i]; return f[x][0]; } inline void dfs(int x,int fa) { for(register int i=head[x];i;i=e[i].nxt) { register int y=e[i].ver; if(y==fa) continue; dfs(y,x); tree[x]+=tree[y]; } if(x!=1) { if(tree[x]==0) ans+=m; if(tree[x]==1) ans++; } } inline int read() { register int x=0,m=1;register char ch=getchar(); while(ch<'0' || ch>'9'){if(ch=='-') m=-1;ch=getchar();} while(ch>='0' && ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();} return x*m; } int main() { n=read(),m=read(); t=log(n)/log(2)+1; for(register int i=1;i<n;i++) { register int x=read(),y=read(); add(x,y),add(y,x); } bfs(); for(register int i=1;i<=m;i++) { register int x=read(),y=read(),LCA=lca(x,y); tree[x]++,tree[y]++,tree[LCA]-=2; } dfs(1,0); printf("%d\n",ans); return 0; }
3.#10132 「一本通 4.4 例 3」异象石(毒瘤)
我们先维护出来一个dis[i]数组表示i到根节点的距离,这个题就好像看起来很好写了。但是我们又想到了一个问题:这个题好像不知道怎么维护答案
我们再看一个东西:如果我们插入一个数x,则这个数对答案的贡献是多少?令path(x,y)=dis[x]+dis[y]-2*dis[lca(x,y)];
如果这个数在查询序列中,排在前面的是l,后面的是r,则对答案的贡献为path(x,r)+path(l,x)-path(l,r)(这个请大家手动画图模拟一下,还是非常好得到的)
那么我们熟出答案就直接输出了吗?手动画图的小伙伴都发现了一个问题:你这个明明维护的是二倍答案啊,那我们输出的时候除以二不就行了吗
这道题就结束了,但是还有一些细节问题:查询序列的维护不适合直接用题目中直接给的点的标号,我们要用dfs序来维护。而且我们维护的查询序列肯定是要以dfs序为关键字单调上升的,所以我们可以用一个set或者手写平衡树来支持查找前驱后继。这就是这道题毒瘤的地方
然后就是代码

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<queue> #include<cmath> #include<set> #define int long long using namespace std; const int N=100001; struct need{ int ver,edge,nxt; }e[N<<1]; int n,t,head[N],m,tot,f[N][31],d[N],dis[N],ans; int dfn[N],cnt[N],total; //dfn[]就是dfs序,cnt[i]存储的是dfs序为i的节点标号 bool vis[N]; queue<int> q; set<int> s; typedef set<int>::iterator IT; IT it; //这个set的用法是现学的,以前没用过,码风可能会毒瘤一些 inline void add(int x,int y,int z) { e[++tot].ver=y,e[tot].edge=z,e[tot].nxt=head[x],head[x]=tot; } inline void bfs() { q.push(1); d[1]=1,dis[1]=0; while(q.size()) { register int x=q.front(); q.pop(); for(register int i=head[x];i;i=e[i].nxt) { register int y=e[i].ver; if(d[y]) continue; d[y]=d[x]+1; dis[y]=dis[x]+e[i].edge; f[y][0]=x; for(register int j=1;j<=t;j++) f[y][j]=f[f[y][j-1]][j-1]; q.push(y); } } } inline int lca(int x,int y) { if(d[x]>d[y]) swap(x,y); for(register int i=t;i>=0;i--) if(d[f[y][i]]>=d[x]) y=f[y][i]; if(x==y) return x; for(register int i=t;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i]; return f[x][0]; } inline void dfs(int x) { dfn[x]=++total; cnt[total]=x; vis[x]=true; for(register int i=head[x];i;i=e[i].nxt) { register int y=e[i].ver; if(vis[y]==true) continue; dfs(y); } } IT l(IT it) { if(it==s.begin()) return --s.end(); return --it; } IT r(IT it) { if(it==--s.end()) return s.begin(); return ++it; } inline int work(int x,int y) { return dis[x]+dis[y]-2*dis[lca(x,y)]; } inline int read() { register int x=0,m=1;register char ch=getchar(); while(ch<'0' || ch>'9'){if(ch=='-') m=-1;ch=getchar();} while(ch>='0' && ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();} return x*m; } signed main() { n=read(); t=log(n)/log(2)+1; for(register int i=1;i<n;i++) { register int x=read(),y=read(),z=read(); add(x,y,z),add(y,x,z); } bfs(); dfs(1); m=read(); for(register int i=1;i<=m;i++) { register char ch[4]; scanf("%s",ch); if(ch[0]=='?') { printf("%lld\n",ans/2); continue; } register int x=read(),y; if(ch[0]=='+') { if(s.size()) { it=s.lower_bound(dfn[x]); if(it==s.end()) it=s.begin(); y=*l(it); ans+=work(x,cnt[y])+work(x,cnt[*it])-work(cnt[*it],cnt[y]); } s.insert(dfn[x]); } else if(ch[0]=='-') { it=s.find(dfn[x]); y=*l(it); it=r(it); ans-=work(x,cnt[y])+work(x,cnt[*it])-work(cnt[y],cnt[*it]); s.erase(dfn[x]); } } return 0; }
那我们这个知识点就讲完啦,再放几道例题(应该是从易到难的吧)
luogu P3258 [JLOI2014]松鼠的新家
luogu P3398 仓鼠找sugar
luogu P1967 货车运输
loj #10133 「一本通 4.4 例 4」次小生成树或者 luogu P4180 [BJWC2010]严格次小生成树
luogu P2680 运输计划
谢谢各位观看到最后~
