写在前面

如果觉得有所收获，记得点个关注和点个赞，感谢支持。
今天遇到有向无环图的一些问题，感觉挺有意思的，而且这些问题的思路特点都差不多，所以想着记录一下。在图论中，如果一个有向图无法从某个顶点出发经过若干条边回到该点，则这个图是一个有向无环图（DAG图）。而提到DAG，就差不多会联想到拓扑排序，拓扑排序是指由某个集合上的一个偏序得到该集合上的一个全序的操作。拓扑排序常用来确定一个依赖关系集中，事物发生的顺序。拓扑排序是对有向无环图的顶点的一种排序，它使得如果存在一条从顶点A到顶点B的路径，那么在排序中B出现在A的后面。DAG在区块链中得到很广泛的应用哦。

概念

图（Graph）是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V, E)，其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。图按照边的有无方向性分为无向图和有向图。

图中某个节点与其他节点的直连边条数称为该节点的度。有向图中，指向其他节点的边成为出度，被其他节点指向的边称为入度。如果在有向图中，无法从某个顶点出发经过若干条边回到该点，则这个图是一个有向无环图（DAG图）。

偏序，集合内只有部分元素之间在这个关系下是可以比较的， 比如：比如复数集中并不是所有的数都可以比较大小，那么“大小”就是复数集的一个偏序关系。全序，集合内任何一对元素在在这个关系下都是相互可比较的，比如：有限长度的序列按字典序是全序的。最常见的是单词在字典中是全序的。

邻接表与邻接矩阵

邻接表和邻接矩阵是图的两种常用存储表示方式，用于记录图中任意两个顶点之间的连通关系，包括权值。下面我们来实际举例一下，对于图 G=(V, E) 而言，其中 V 表示顶点集合，E 表示边集合。给定了概念之后，对于无向图 graph，图的顶点集合和边集合如下：



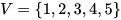
对于有向图 digraph，图的顶点集合和边集合如下：

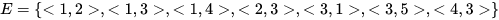
邻接表

无向图 graph 表示

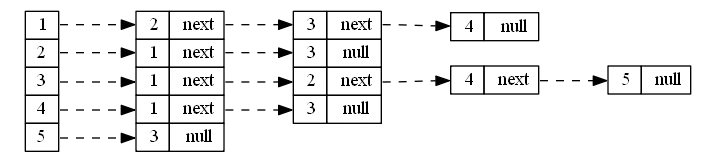
有向图 digraph 表示

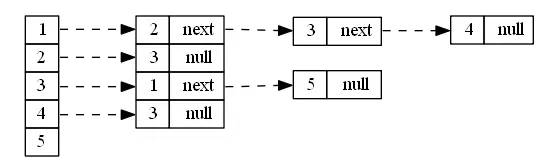
若采用邻接表表示，则需要申请 $|V|$ 个列表，每个列表存储一个顶点出发的所有相邻顶点。如果图 $G$ 为有向图，则 $|V|$ 个列表存储的总顶点个数为 $|E|$ ；如果图 $G$ 为无向图，则 $|V|$ 个列表存储的总顶点个数为 $2|E|$ （暂不考虑自回路）。因为需要申请大小为 $|V|$ 的数组来保存节点，对节点分配序号，所以需要申请大小为 $|V|$ 的额外存储空间，即邻接表方式的存储空间复杂度为 $O(|V|+|E|)$ 。

邻接矩阵

无向图 graph 表示

有向图 digraph 表示

若采用邻接矩阵表示，则需要申请空间大小为 $|V|^2$ 的二维数组，在二位数组中保存每两个顶点之间的连通关系，则无论有向图或无向图，邻接矩阵方式的存储空间复杂度皆为 $O(|V|^2)$ 。若只记录图中顶点是否连通，不记录权值大小，则可以使用一个二进制位来表示二维数组的每个元素，并且根据无向图的特点可知，无向图的邻接矩阵沿对角线对称，所以可以选择记录一半邻接矩阵的形式来节省空间开销。

根据邻接表和邻接矩阵的结构特性可知，当图为稀疏图、顶点较多，即图结构比较大时，更适宜选择邻接表作为存储结构。当图为稠密图、顶点较少时，或者不需要记录图中边的权值时，使用邻接矩阵作为存储结构较为合适。

拓扑排序

拓扑排序：就是一个有向无环图的所有定点的线性序列。如果在图中，有一条从A点到B点的路线，那么在拓扑排序中，点A一定排在点B的前面。这个东西，是比较难理解，再上图说话吧。比如在这个有向无环图中，它用拓扑排序，该怎么进行呢？

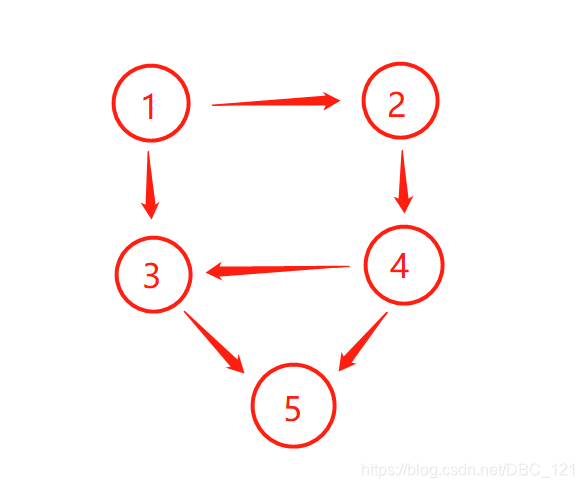
• 先找一个起点，很明显，这个起点就1号点了，因为这个点，没有任何其他指向它的路线。如果存在多个这样的点，那么随意输出就可以了，也就是说，可能存在多个拓扑序列。
• 然后将这个起点删除，并同时删除这个起点发射出去的路线。
• 重复上面两个步骤，直到这张有向无环图的所有点都被删除干净。

如果到某个阶段，发现当前图中不存在像1号点这样的起点了，那么这张图就不是有向无环图了。最后，一个完整的拓扑排序就完成了，结果为：1、2、4、3、5。

代码实现

为了更方便理解，我们这里直接贴出一道题，根据这道题的实现代码来体会，这道题是完全按照拓扑排序的思路进行解答的。题目如下

解题思路

• 本题可约化为： 课程安排图是否是 有向无环图(DAG)。即课程间规定了前置条件，但不能构成任何环路，否则课程前置条件将不成立。
• 思路是通过 拓扑排序 判断此课程安排图是否是 有向无环图(DAG) 。 拓扑排序原理： 对 DAG 的顶点进行排序，使得对每一条有向边 $(u, v)$ ，均有 $u$（在排序记录中）比 $v$ 先出现。亦可理解为对某点 $v$ 而言，只有当 $v$ 的所有源点均出现了， $v$ 才能出现。

算法流程

• 统计课程安排图中每个节点的入度，生成 入度表 indegrees。
• 借助一个队列 queue，将所有入度为 0 的节点入队。
• 当 queue 非空时，依次将队首节点出队，在课程安排图中删除此节点 pre：
  • 并不是真正从邻接表中删除此节点 pre，而是将此节点对应所有邻接节点 cur 的入度 −1，即 indegrees[cur] -= 1。
  • 当入度 −1后邻接节点 cur 的入度为 0，说明 cur 所有的前驱节点已经被 “删除”，此时将 cur 入队。
• 在每次 pre 出队时，执行 numCourses--；
  • 若整个课程安排图是有向无环图（即可以安排），则所有节点一定都入队并出队过，即完成拓扑排序。换个角度说，若课程安排图中存在环，一定有节点的入度始终不为 0。
  • 因此，拓扑排序出队次数等于课程个数，返回 numCourses == 0 判断课程是否可以成功安排。

算法可视化

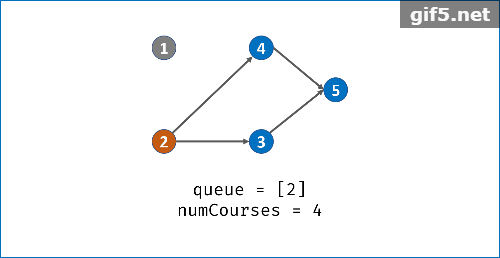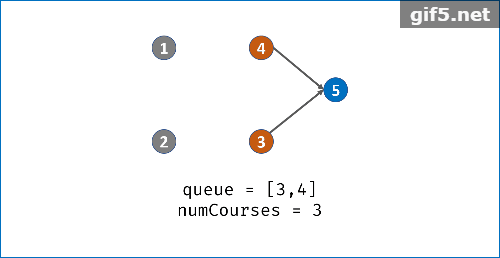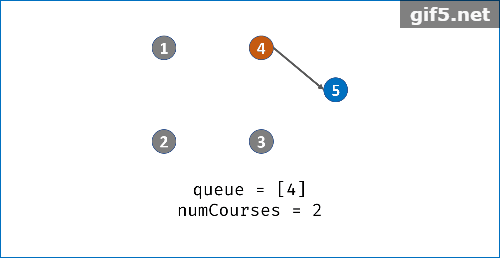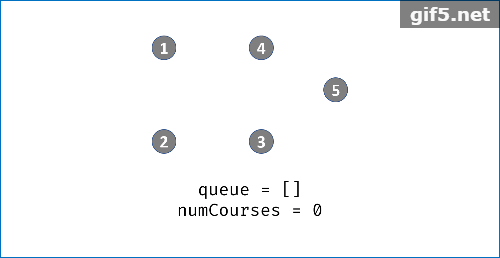
实现

public boolean canFinish(int numCourses, int[][] prerequisites) {
    int[] indegrees = new int[numCourses];
    List<List<Integer>> adjacency = new ArrayList<>();
    Queue<Integer> queue = new LinkedList<>();
    for(int i = 0; i < numCourses; i++)
        adjacency.add(new ArrayList<>());
    
    for(int[] cp : prerequisites) {
        indegrees[cp[0]]++;
        adjacency.get(cp[1]).add(cp[0]);
    }
    
    for(int i = 0; i < numCourses; i++)
        if(indegrees[i] == 0) queue.add(i);
    
    while(!queue.isEmpty()) {
        int pre = queue.poll();
        numCourses--;
        for(int cur : adjacency.get(pre))
            if(--indegrees[cur] == 0) queue.add(cur);
    }
    return numCourses == 0;
}