【基于C++的非线性方程的解法研究及实现】

【前言】

关于非线性方程f(x) = 0的根的解法目前分为三类，二分法，试值法和不动点迭代法

本文实例为寻找f(x) = x² - 2x在区间[-1, 3]内精度在0.05以内的实根

代码中的set用于保存答案

【1.二分法】

二分法又称二分区间法，是求解非线性方程近似根的一种常用的简单方法。

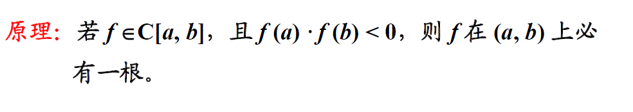
算法：

【代码实现】

inline float f(float x) { return x * x - 2 * x; }
inline float binary_search(float l, float r, float k) {
	float left = l, right = r;
	while (true) {
		float x = (left + right) / 2;
		float fa = f(left), fx = f(x);
		if (fa * fx < 0) right = x;
		else left = x;
		if (abs(right - left) <= 2 * k) return x;
	}
}
inline void solve_division(float l, float r, float k) {
	set<float> ans;
	for (float i = l; i < r; i += k) {  //将区间分为(r - l) / k个分别进行查找
		float fa = f(i), fb = f(i + k);
		if (fa == 0) ans.insert(i);
		else if (fb == 0) ans.insert(i + k);
		else if (fa * fb < 0)  ans.insert(binary_search(i, i + k, k));
	}
	cout << "The root of the equation is(division):" << endl;
	for (auto& it : ans) {
		printf("%.2f\n", it);
	}
}

【2.试值法】

该算法与二分法的不同点在于将二分法中x = (a + b) / 2换做如下操作

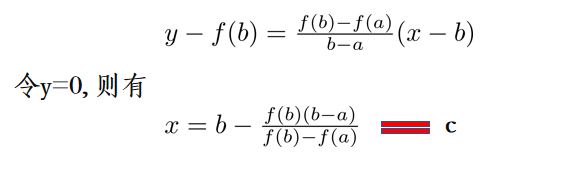
【代码实现】

inline float tryvalue_search(float l, float r, float k) {
	float left = l, right = r;
	while (true) {
		float x = right - (right - left) * f(right) / (f(right) - f(left));  // 不同点
		float fa = f(left), fx = f(x);
		if (fa * fx < 0) right = x;
		else left = x;
		if (abs(right - left) <= 2 * k) return x;
	}
}
inline void solve_tryvalue(float l, float r, float k) {
	set<float> ans;
	for (float i = l; i < r; i += k) {
		float fa = f(i), fb = f(i + k);
		if (fa == 0) ans.insert(i);
		else if (fb == 0) ans.insert(i + k);
		else if (fa * fb < 0) {
			float x = tryvalue_search(i, i + k, k);
			ans.insert(x);
		}
	}
	cout << "The root of the equation is(tryvalue):" << endl;
	for (auto& it : ans) {
		printf("%.2f\n", it);
	}
}

【3.不动点迭代法】

大致意思就是由f(x) = 0建立一个函数g(x) = x，让x1 = g(x0), x2 = g(x1), x3 = g(x2) … xn = g(n - 1)…由于当n趋于无穷时若xn = g(n)，那么若xi = g(xi)可得xi为f(x)的一个实根

扫描二维码关注公众号，回复： 10935362 查看本文章

那么以f(x) = x² - 2x为例

g1(x) = x² / 2
g2(x) = sqrt(2x)
g3(x) = x² - x

由于不知道函数是否发散，我们设置一个迭代次数cnt，表示若cnt次内未收敛返回空值

由于x0的取值不确定，我们同样将区间分为(r - l) / k个，对于每个端点值进行cnt次的迭代

【代码实现】

#define eps 1e-6
typedef float(*ff)(float);
inline float judge(float x) { return abs(x) <= eps ? 0 : x; }  //当数值小于1e-6是认为它是0
inline float g1(float x) { return x * x / 2; }
inline float g2(float x) { return sqrt(2 * x); }
inline float g3(float x) { return x * x - x; }
inline void g_iteration(double x, double k, int cnt, ff g, set<float>& s) {
	if (!judge(x - g(x))) {
		s.insert(judge(x));
		return;
	}
	if (!cnt) return;
	g_iteration(g(x), k, cnt - 1, g, s);
}
inline void solve_iteration(float l, float r, float k, int cnt, ff g) {
    //cnt为迭代次数
	set<float> ans;
	for (float i = l; i < r; i += k) {
		g_iteration(g(i), k, cnt, g, ans);
	}
	cout << "The root of the equation is(solve_iteration):" << endl;
	for (auto& it : ans) {
		printf("%.6f\n", it);
	}
}

【程序源码】

#include <bits/stdc++.h>
using namespace std;
#define eps 1e-6
typedef float(*ff)(float);
inline float f(float x) { return x * x - 2 * x; }
inline float binary_search(float l, float r, float k) {
	float left = l, right = r;
	while (true) {
		float x = (left + right) / 2;
		float fa = f(left), fx = f(x);
		if (fa * fx < 0) right = x;
		else left = x;
		if (abs(right - left) <= 2 * k) return x;
	}
}
inline void solve_division(float l, float r, float k) {
	set<float> ans;
	for (float i = l; i < r; i += k) {
		float fa = f(i), fb = f(i + k);
		if (fa == 0) ans.insert(i);
		else if (fb == 0) ans.insert(i + k);
		else if (fa * fb < 0)  ans.insert(binary_search(i, i + k, k));
	}
	cout << "The root of the equation is(division):" << endl;
	for (auto& it : ans) {
		printf("%.2f\n", it);
	}
}
inline float tryvalue_search(float l, float r, float k) {
	float left = l, right = r;
	while (true) {
		float x = right - (right - left) * f(right) / (f(right) - f(left));
		float fa = f(left), fx = f(x);
		if (fa * fx < 0) right = x;
		else left = x;
		if (abs(right - left) <= 2 * k) return x;
	}
}
inline void solve_tryvalue(float l, float r, float k) {
	set<float> ans;
	for (float i = l; i < r; i += k) {
		float fa = f(i), fb = f(i + k);
		if (fa == 0) ans.insert(i);
		else if (fb == 0) ans.insert(i + k);
		else if (fa * fb < 0) {
			float x = tryvalue_search(i, i + k, k);
			ans.insert(x);
		}
	}
	cout << "The root of the equation is(tryvalue):" << endl;
	for (auto& it : ans) {
		printf("%.2f\n", it);
	}
}
inline float judge(float x) { return abs(x) <= eps ? 0 : x; }
inline float g1(float x) { return x * x / 2; }
inline float g2(float x) { return sqrt(2 * x); }
inline float g3(float x) { return x * x - x; }
inline void g_iteration(double x, double k, int cnt, ff g, set<float>& s) {
	if (!judge(x - g(x))) {
		s.insert(judge(x));
		return;
	}
	if (!cnt) return;
	g_iteration(g(x), k, cnt - 1, g, s);
}
inline void solve_iteration(float l, float r, float k, int cnt, ff g) {
	set<float> ans;
	for (float i = l; i < r; i += k) {
		g_iteration(g(i), k, cnt, g, ans);
	}
	cout << "The root of the equation is(solve_iteration):" << endl;
	for (auto& it : ans) {
		printf("%.6f\n", it);
	}
}
int main() {
	solve_division(-1, 3, 0.05);
	solve_tryvalue(-1, 3, 0.05);
	cout << "g1:" << endl;
	solve_iteration(-1, 3, 0.05, 50, g1);
	cout << "g2:" << endl;
	solve_iteration(-1, 3, 0.05, 50, g2);
	cout << "g3:" << endl;
	solve_iteration(-1, 3, 0.05, 50, g3);
	return 0;
}

【运行结果】

【结果分析】

可以看到三种方法均能够找到该方程的近似根，在不动点迭代法中，g1只能找到根x = 0，而g2和g3可以找到根x = 0和x = 2