本文介绍了逻辑回归算法的原理和推导。主要包括：问题引入，交叉熵误差，逻辑回归梯度的误差计算和梯度下降算法。

10. Logistic Regression

10.1 Logistic Regression Problem

上一节课，我们介绍了Linear Regression线性回归，以及用平方错误来寻找最佳的权重向量w，获得最好的线性预测。本节课将介绍Logistic Regression逻辑回归问题。

在心脏病是否复发二元分类问题中，其输出空间只含有两项{+1，-1}（复发和不发复发）。在有噪声的情况下，机器学习流程如下图所示。

目标函数 $f(x)$ 可以使用目标分布 $P$ 来表示，公式如下：

通常情况下，会以概率的方式告知患者复发的可能性，下图中，该患者心脏病复发的可能性为80%。

这种情况被称为软二元分类（soft binary classification），目标函数 $f(x)$ 如下式所示，输出为概率。

扫描二维码关注公众号，回复： 10954167 查看本文章

针对该目标函数，理想数据集和实际数据集的对比如下：

理想数据集的情况是预测输出都是概率的形式，针对心脏病是否复发的例子来说，真实的数据只有复发和没复发两种情况，而不会在病例中记录病发的概率。

可以将实际训练数据看做含有噪音的理想训练数据。问题就转化为：如何使用真实的训练数据解决软二元分类问题，即假设函数如何设计。

首先回忆两种假设函数（二元分类和线性回归）中都具有的是哪部分？答案是求输入 $X = [x_0,x_1,...,x_d]$ 各属性的加权总分数（score），公式如下：

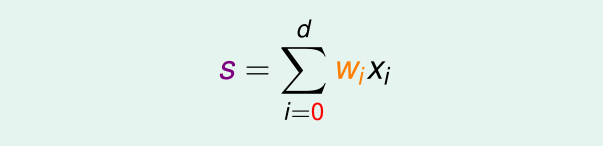
如何把该得分从在整个实数范围内转换成为一个0~1之间的值呢？此处就引出了本章的主题，logistic函数（logistic function）用 $\theta(s)$ 表示。分数s越大风险越高，分数s越小风险越低。假设函数 $h(x)$ 如下所示。

逻辑回归函数：

由此易知，通过logistic函数 $\theta(s)$ 可以将值域从实数集 $R$ 映射到 （0,1）区间内。逻辑回归函数是平滑（处处可微）、单调的S形（sigmoid）函数，因此又被称为sigmoid函数。

通过logistic函数，将软二元分类的假设函数近似为目标函数 $f(x) = P(+1|x)$：

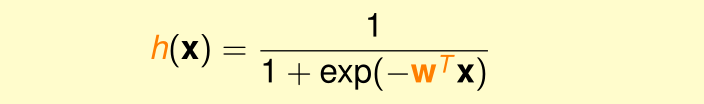
习题1：

10.2 Logistic Regression Error

首先看一下二元分类、线性回归与逻辑回归的对比：

分数 $s$ 是在每个假设函数中都会出现的 $W^TX$ ，前两个学习模型的错误衡量分别对应着0/1误差和平方误差，而逻辑回归所使用的err函数是本节要介绍的内容。

先介绍一下 “似然（likelihood）” 的概念。对于目标函数 $f(x) = P(+1|x)$，如果找到了 hypothesis 很接近 target function（err很小）。亦即在Hypothesis集合中找到一个hypothesis $g$ 与 target function 最接近，能产生同样的数据集D，包含样本真实输出y，则称这个 hypothesis $g$ 是最大似然函数 $g$ 。公式表示如下：

由逻辑回归的目标函数可推导出下式成立：

考虑一数据集 $D = \{(x_1,◦),(x_2,×), . . . ,(x_N,×)\}$，则通过目标函数产生此种数据集样本的概率可以用下式表示：

由目标函数 $f$ 的公式做如下替换：

目标函数 $f$ 是未知的，已知的只有假设函数 $h$，应用最大似然函数公式 $g = argmax_h \ likelihood(h)$ 可以将假设函数 $h$ 代替目标函数 $f$：

$likelihood(h) = P(x_1)h(x_1) × P(x_2)(1 − h(x_2)) × . . .P(x_N)(1 − h(x_N))$

逻辑回归的假设函数 $h(x) = θ(w^Tx)$ 有性质： $1 − h(x) = h(−x)$，因此可以将上式进一步转化为：

$likelihood(h) = P(x_1)h(+x_1) × P(x_2)h(−x_2) × . . .P(x_N)h(−x_N)$

因为 $P(x_i), i=1,2,...,N$ 对所有的 $h$ 来说都相同，即 $h$ 的似然只与函数 $h$ 对每个样本的连乘有关，所以可以忽略这一项。将样本真实输出 $y_n$ （+1，-1）引入公式，可得下式成立：

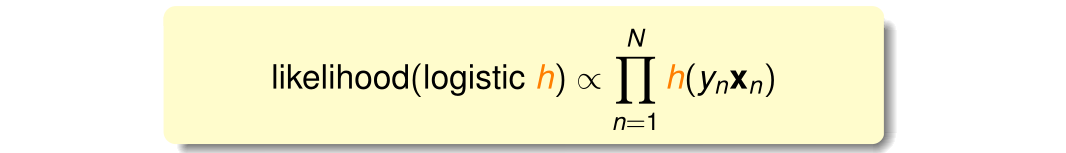
寻找的是似然最大的假设函数h，因此得到下式：

由逻辑回归的假设函数公式 $h(x) = θ(w^Tx)$ 可得：

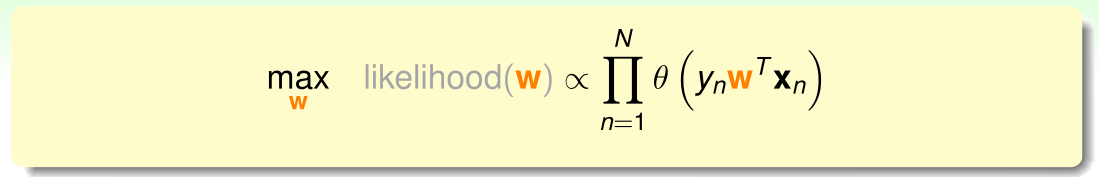
连乘公式不容易求解最大问题，因此对上式取对数，以便将问题转换为连加的形式：

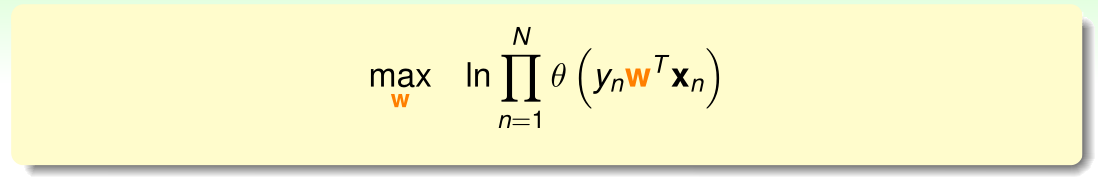
通过引入符号，将最大化问题转化为最小化问题，同时引入平均系数 $\frac 1N$使得公式与之前的错误衡量类似：

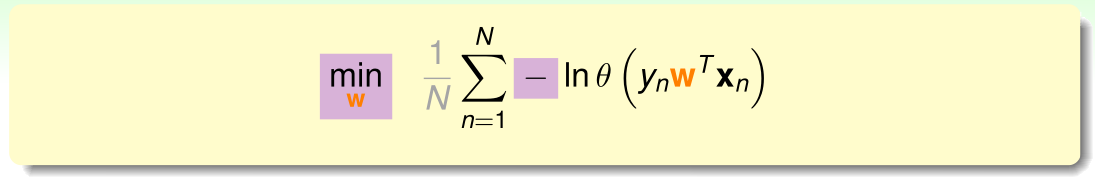
将 $\theta (s)$ 代入上式，公式进一步转换为：

至此推到结束，由上式可得逻辑回归的误差函数，称为交叉熵误差函数（cross-entropy error），公式为：
$err(w,x,y) = ln(1 + exp(−ywx))$

习题2：

10.3 Gradient of Logistic Regression Error

推导出logistic回归的 $E_{in}(w)$ 之后，接下来寻找使得 $E_{in}(w)$ 最小的权值向量 $w$。 $E_{in}(w)$ 的公式如下：

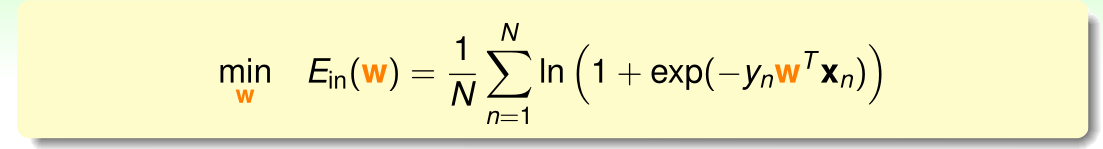
回顾在上一节线性回归中提到的 $E_{in}(w)$ 的曲线图：

由函数公式和图像可知，该函数为连续（continuous）可微（differentiable）的凹函数，因此其最小值在梯度为零时取得，即 $\nabla E_{in}(w) =0$ 。

要求解 $\nabla E_{in}(w)$ ，需要对权值向量 $w$ 的各个分量求偏微分，复杂公式求解偏微分可以使用“链式法则”。

为了强调公式中符号的临时性，不使用字母表示，而用临时符号□和○表示：

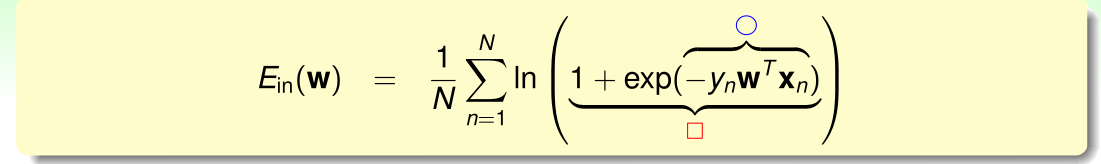
求解过程（ $\theta$ 函数为ogistic函数）：

计算结果：

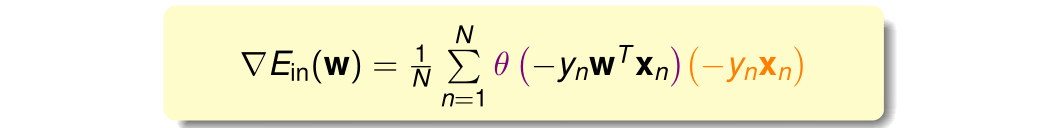
由于 $E_{in}(w)$ 为凹函数，令 $\nabla E_{in}(w) = 0$，求出权值向量 $w$，该向量即可使得函数 $E_{in}(w)$ 最小。

上式中，可以把 $\nabla E_{in}(w)$ 看做 $θ(−y_nw^Tx_n)$ 与 $−y_nx_n$ 的线性加权和，要使 $\nabla E_{in}(w) = 0$，有两种情况成立。分别是线性可分的情况和线性不可分的情况。

对于线性可分的情况，令所有权重 $θ(−y_nw^Tx_n) = 0$，即可保证梯度 $\nabla E_{in}(w) = 0$ 。 $\theta$ 函数是sigmoid函数（S型函数），只要让自变量 $−y_nw^Tx_n$ 趋于 $- \infin$ 即可，即 $y_nw^Tx_n \gg 0$ 。该式对于所有的样本点成立的条件是： $y_n$ 与 $w^Tx_n$ 同号。这表示数据集D必须是全部线性可分的才能成立。

真实的数据绝大多数情况是线性不可分的。这种情况没有解析解，因此需要通过迭代优化方法（iterative optimization approach）来求解。首先回顾一下PLA，然后引出逻辑回归梯度的计算方法。

$w$ 每次更新两部分：一个是每次更新的方向 $y_nx_n，$ 用 $v$ 表示，另一个是每次更
新的步长 $\eta$ 。参数 $(v, \eta)$ 和终止条件决定了迭代优化算法。

习题3：

10.4 Gradient Descent

Logistic回归求解最小的 $E_{in}(w)$ 使用类似PLA的迭代优化方法，通过一步一步改变权值向量 $w$，寻找使得 $E_{in}(w)$ 最小的变权值向量 $w$，迭代优化方法的更新公式如下所示：

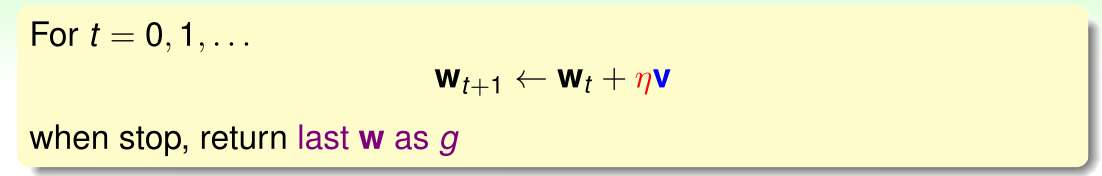
上式中， $v$ 表示更新的方向， $\eta$ 表示更新的步长。Logistic回归的 $E_{in}(w)$ 为处处可微的凹函数，其曲线的“谷底”对应的 $w$ 可使得 $E_{in}(w)$ 最小。

那么应该如何选择这两个参数使得更新公式尽可能快得到达该点呢？

在 $\eta$ 固定的情况下，如何选择 $v$ 的方向保证更新速度最快？按照 $E_{in}(w)$ 最陡峭的方向修正。即在 $\eta$ 固定， $|v| = 1$ 的情况下，以最快的速度（有指导方向）找出使得 $E_{in}(w)$ 最小的 $w$，公式如下：

以上是非线性带约束的公式，寻找最小 $w$ 仍然非常困难，考虑将其转换成一个近似的公式，通过寻找近似公式中最小的 $w$，达到寻找原公式最小的 $w$ 的目的，此处使用到泰勒展开（Taylor expansion）：

利用微分思想和线性近似，假设每次下山只前进一小步，即 $\eta$ 很小，根据泰勒公式一阶将上式展开可以得到：
$\approx E_{in}(w_t) + ((w_t+ ηv) - w_t) \frac{\nabla E_{in}(w_t)} {1!}$
$≈ E_{in}(w_t) + ηv^T∇E_{in}(w_t)$
进一步转化为：

该公式中 $E_{in}(w_t)$ 是已知的，而 $\eta$ 为给定的大于零的值，因此求解上式最小化的问题又可转换为：

迭代的目的是让 $E_{in}(w_t)$ 越来越小，即让 $E_{in}(w_t + \eta v) < E_{in}(w_t)$ 。 $\eta$ 是标量，因为如果两个向量方向相反，则它们的内积最小（为负）；也就是说，如果梯度更新的方向 $v$ 与梯度 $∇E_{in}(w_t)$ 反向的话，就能保证每次迭代 $E_{in}(w_t + \eta v) < E_{in}(w_t)$ 都成立。于是，可令梯度下降方向 $v$ 为：

$v$ 是单位向量，每次都沿着梯度的反方向更新，这种优化方法称为梯度下降（gradient descent），这是一种常用且简单的方法。实际应用中常常使用随机梯度下降算法（SGD）。

更新方向参数 $v$ 的更新方式决定后，再看看更新步长参数 $\eta$ 的取值对梯度下降的影响：

$\eta$ 太小时,下降速度很慢，因此寻找最优 $w$ 的速度很慢，如左图所示； $\eta$ 太大时，会造成下降不稳定，甚至会出现不降反增的情况，如中间图所示。因此，合适的 $\eta$ 应为随着梯度的减小而减小，如右图所示，即参数 $\eta$ 是可变的，且与梯度大小 $||∇E_{in}(w_t)||$ 成正比。由此，可给出更新步长 $\eta$ 的计算公式：

最终公式记为：

此时的 $\eta$ 被称为固定的学习率（fixed learning rate） ，公式称为固定学习率的梯度下降。
至此，我们可以总结梯度下降算法的计算流程。伪代码如下：

• 权重初始化：初始化权重向量 $w$ 为 $w_0$；
• 计算梯度： $\nabla E_{in}(w_t)$；
• 迭代更新： $w_{t+1} \leftarrow W_t - \eta \nabla E_{in}(w_t)$
• 计算终止：满足 $\nabla E_{in}(w_t) \approx 0$ 或到达迭代次数时，迭代结束；

习题4：

Summary

本节课共四小节，介绍了如下内容：
第一小节从逻辑回归问题出发，将 $P(+1|x)$ 作为目标函数，使用逻辑回归函数 $\theta (w^Tx)$ 形式的假设函数；
第二小节介绍了逻辑回归即误差函数，称为交叉熵误差；
第三、四小节介绍了通过梯度下降算法计算逻辑回归的误差。

参考：
https://www.cnblogs.com/ymingjingr/p/4306666.html
https://github.com/RedstoneWill/HsuanTienLin_MachineLearning