上回我们说到了算法在“排序“问题上是如何施展魔法的,下面我们闲话少叙,继续去讨论算法在不同问题上发挥的作用,让你对算法的概念有更深的理解。
路径问题
先介绍什么是图。在现实生活中,我们想要达到什么目的,往往不能一蹴而就,有的时候需要有序的先达到一个甚至几个前提条件,才能达到最后的目的。举个例子,我们想要去北京,南京,上海,杭州这四地去旅游,我们就需要选择一个城市为起点,一个城市为终点,并终确定一个旅行的路径。而其实每条路径都是有成本的,简单说包括车票钱以及路上消耗的时间。图就是由各个城市(节点)以及路径(边)组成的,加权图就是在每个边上添加一个成本(权重)。
再介绍一种数据结构。要在计算机中表示一个图,就得说一种叫做散列表的数据结构。熟悉C语言的你肯定知道如何实现一个哈希表,它是由数组链表组合而成,每个数组项存储着一个链表。它就是散列表,你想象一个所有链表都有一个元素的哈希表(哈希函数对不同的输入都有唯一不同解,不存在冲突的问题),它提供一种由A查到B快速的映射关系,这种数据结构正好帮我们去在计算机中表示图。散列表再多说两句,在程序需要防止重复数据项出现(插入前需要查询数据是否在数据结构中)或者诸如网站缓存页面这些需求,数据结构的选择都是散列表。
概念介绍完了,我们开始解决实际问题。我们先入手一个简单的问题:查找最短路径。在一个图的关系中,我们有确定的起点和终点,且每条边都没有权重,我们需要找出最由起点到终点经历边最少的路径数,亦或这个最少路径经历的边数是无穷大(无法到达)。我们使用广度优先搜索算法来解决这个问题。算理很简单,我们将关系分层(广度),与起点直接相连的为广度1节点,需要经过广度1的节点到达的节点称为广度2节点。我们按照广度优先的策略,一层一层的筛选与起点相关联的节点,如果在筛选的过程中遇到了终点,那么我们就找到了最短路径(最小的广度),如果所有的节点都搜索完了,依然没有找到终点,那很遗憾,并没有由起点到终点的路径。
# beijing--------------->shanghai---->hangzhou
# - - -
# - - -
# ->nanjing--------------
#
# 代码没有把最找到的最短路径打出来,你可以尝试着更改代码将其打印出来
from collections import deque
graph={}
graph["beijing"] = ["shanghai", "nanjing"]
graph["shanghai"] = ["hangzhou"]
graph["nanjing"] = ["shanghai","hangzhou"]
graph["hangzhou"] = []
def search(name):
search_queue = deque()
search_queue += graph[name]
searched = []
while search_queue:
city=search_queue.popleft()
if city not in searched:
if City_is_End(city):
print "We reach "+ city + "!"
return True
else:
search_queue += graph[city]
searched.append(city)
return False
def City_is_End(name):
return name=='hangzhou'
search("beijing")
Dijkstra’s algorithm
让我们先来把问题理清楚。问题的本质是以物换物,在一个跳蚤市场,所有的交易都是在物品交换的基础上再支付一部分金钱。你想要的是一架钢琴,你手中有的是一本乐谱。钢琴的主人不接受乐谱作为交互物品,他只接受用吉他或者架子鼓再支付一部分金钱才能交换,那我们怎么办呢?我们在逛了跳蚤市场发现,我们的乐谱支付5块钱可以换一个黑胶唱片,而黑胶唱片再支付15块钱就可以换一个低音吉他!于是我们可以几经周折通过乐谱再额外支付一些金钱来换一把钢琴!但随着你对跳蚤市场货物的交换规则的了解不断增加,你发现不止着一条路可以帮助你换得钢琴。我们来绘制一个图,把大家的交换意愿表示出来。

根据这个交易意愿,我们能获得一张表示这张图的表,我们命名为GRAPH,举个例子,针对乐谱,我们建立其与黑胶唱片与海报的映射关系,并存储这个映射关系的消耗为5和0。
Dijkstra算法的核心是针对图中的每一个节点,我们都找到由其所有前序节点能到达的最便宜的路径,这样最后我们将从终点一步步往前推,就能得到由起点到终点最短的路径。这里我们做两个表,一个表存储由这个节点的前序节点到此节点的最小开销值,名为Cost。另一个表我们存储这一节点与最小开销的前序节点的映射关系,名为PARENTS。下图对一个由起点,A,B,终点构成的有向无环图与对应的三个表。它是我们实际问题的简单抽象。你要适应这种实际问题的抽象,它能帮助从繁杂的重复工作中解放出来,抓住问题的本质。


算理是我们从Cost表中找到找到消耗最小的节点B(这非常重要,一定要确保是消耗最小的),从Graph中得到它的后续节点信息,得到经由它到各个后序节点的距离,如果跟原Cost表相比更小,则更新Cost表与Parents表。点B到A与终点的距离分别为5与7,与原Cost表相比都更为小,于是更新Cost列表与Parents列表如下:
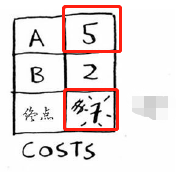
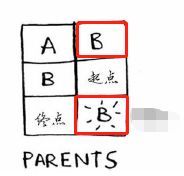
我们继续从Costs表中找出没有做过此运算的且消耗最小的节点,只剩下A节点了(终点没有后续节点,不用做此操作),我们得到经由A到终点的距离为6,比当前Costs列表中的7要小,于是更新Cost表以及PARENTS表如下:
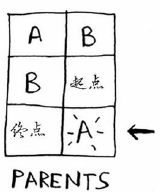
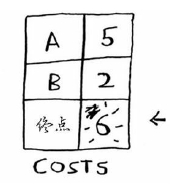
至此,Cost表中再无节点需要做操作,则表Costs与Parents不需在做更新,则由Parents表即可得消耗最短的路径:终点–>A–>B–>起点。
graph={}
graph["start"]={}
graph["start"]["a"]= 6;
graph["start"]["b"]= 2;
graph["a"]={}
graph["a"]["fin"]=1
graph["b"]={}
graph["b"]["a"]=3
graph["b"]["fin"]=5
graph["fin"]={}
infinity = float("inf")
costs = {}
costs["a"] = 6
costs["b"] =2
costs["fin"]=infinity
parents ={}
parents["a"]="start"
parents["b"]="start"
parents["fin"]=None
processed=[]
def find_lowest_cost_node(costs):
lowest_cost=float("inf")
lowest_cost_node=None
for node in costs:
cost = costs[node]
if cost < lowest_cost and node not in processed:
lowest_cost = cost
lowest_cost_node =node
return lowest_cost_node
node = find_lowest_cost_node(costs)
while node is not None:
cost = costs[node]
neighbors = graph[node]
for n in neighbors.keys():
new_cost=cost + neighbors[n]
if costs[n] > new_cost:
costs[n] = new_cost
parents[n] = node
processed.append(node)
node= find_lowest_cost_node(costs)
print parents
如果你把现实的问题用图表现出来的时候,发现有的边上边的权值是负值,那么Dijkstra算法将会失效,这是因为你从Costs表中找到的消耗最低的节点将不是真正最低的。
P≠NP
NP的全拼为Non-deterministic Polynomial,NP类问题指的由是所有的非确定性多项式时间可解的判定问题构成的问题,简单来说,这类问题除了暴力的穷举所有可能性并验证这种可能性的正确性这种解决方法,没有其他捷径。相对的所有可以在多项式时间内求解的判定问题构成P类问题,简单说就是由捷径,可计算的问题。举个例子,上边我们讨论的能被Dijkstra算法解决的问题,就是P类问题,我们针对这种问题不用找出所有的可能路径去比较总消耗,我们可以把问题分割成小问题逐个击破。
我们现在举一个NP问题的例子,假设你有一个由电台为元素构成的集合A,你还有一个由城市名称构成的集合B。集合A中的每一个电台都会包含城市集合B中的部分城市,现在让你以最少消耗集合A中的电台数量的代价,选出包含所有城市集合B的电台集合C。这个问题就是一个NP问题。
不过我们针对这种NP问题,也不是束手无策。我们可以采取贪婪策略,贪婪策略寻找局部的最优解,企图以这种方式去获得全局的最优解,继续说回刚才的NP问题例子,我们可以这么编写代码去解决这个问题:我们不断的遍历电台集合,从中找到覆盖当前未被覆盖的城市中最多城市数的单台,直到将所有的城市覆盖,下面是对应的代码:
states_needed = set(["mt","wa","or","id","nv","ut","ca","az"])
stations={}
stations["kone"]=set(["id","nv","ut"])
stations["ktwo"]=set(["wa","id","mt"])
stations["kthree"]=set(["or","nv","ca"])
stations["kfour"]=set(["nv","ut"])
stations["kfive"]=set(["ca","az"])
final_stations=set()
while states_needed:
best_station = None
states_covered=set()
for station,states_for_station in stations.items():
covered = states_needed & states_for_station
if len(covered) > len(states_covered):
best_station=station
states_covered=covered
final_stations.add(best_station)
states_needed-=states_covered
print final_stations
穷举的方法时间消耗用大O表示法为O(2n),而使用贪婪策略,得到结果的时间为O(n2)。
贪婪策略得出来的可能不是最优解,但是他肯定是近似的最优解,而且所消耗的时间远比要得到最优解的方法低得多,所以对一些NP问题,采取贪婪策略不失为上上策。
这里简单介绍一下另一个NP问题,旅行商问题。问题讲的是有确定的城市,但是起点和终点城市,有一个旅行商要游历所有的城市,并且确保旅程最短。这个问题要求得最优解,他的时间是O(n!)。
如果能在遇到问题的时候,能够准确的识别出来是NP问题,那我们就可以不用浪费时间去思考有没有解决问题的捷径,反而致力于求得问题的近似最优解。但是遗憾的是,目前还没有行之有效的办法让我们用来判断问题的类型,不过我们通过分析问题的特征,有助于帮助我们归类问题属于NP还是P。
- 涉及"所有组合"的问题通常是NP完全问题
- 如果问题可以转换为集合覆盖问题或者旅行商问题,那么它肯定是NP完全问题
