前言
书中这部分讲的太快,并且未能和已有知识做足够的联系,乍看起来还是有点不好理解的。
但如果联系了实际的物理意义以及向量叉乘等已有知识后,就变得好理解了。
另外,推导公式的确有利于理解,作者或许也是为此才出的这些习题吧。
推导过程中用到的知识:
1、分块矩阵运算。
2、向量叉积性质,二重叉积、反交换律等。
文中推导,均是笔者手推,水平有限,如有纰漏,还望不吝赐教。
1、验证SO(3)、SE(3)和Sim(3)关于乘法成群。
(1)SO(3)为三纬旋转矩阵构成的特殊正交群。
根据群的定义(一种结合加一种运算),书中定义式式4.1可以表示集合,运算选择乘法;
将以上依次代入性质群性质1-4,性质12显然满足;选幺元为33单位阵
,性质34显然也满足;
(2)SE(3)为变换矩阵构成的特殊欧氏群。
根据群的定义,书中定义式式4.2表示群的集合,运算选择乘法;
性质1 显然。
性质2 矩阵的结合律也容易得到(可以展开看看,一目了然)。
性质3 选幺元为44单位阵
,显然满足。
性质4 根据分块矩阵求逆公式
令
,
显然
也属于SE(3),并且
,于是性质4满足;
(3)仿照(2)很容易可以验证。
2、验证 构成李代数。
将此李代数视为3维向量,利用向量相关性质,性质1-3均容易得到。
对于性质4,利用向量二重叉积公式,将下面三式相加,立得。
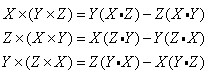
值得一提的是,向量点积结果为标量,满足交换律。
3、验证 和 满足李代数要求的性质。
(1)
先来看看其李括号是啥意思

根据上面的推导,结合问题2,性质1-4容易得到。
(2)
性质1-3容易得到,讨论性质4。
其中利用了(1)中所推导的李代数
的李括号为矢量叉积。

4、验证性质(4.20)和(4.21)
(1)性质(4.20)直接展开即可得到。
(2)性质(4.21)也很明显,书中写的比较清楚了,
记得用
就行了,直接展开立即得到。
5、证明
这实际属于向量的相似变换,
可以参考我讲角速度相似变换定理的博文: 角速度的相似变换定理的证明.
6、
(1)对于SO(3)的伴随性质
根据P79的(4.22),

(2)对于SE(3)的伴随性质
Step1 由定义,可得
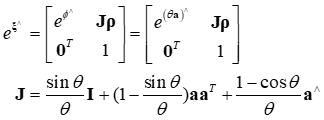
Step2 等式左边

Step3 等式右边
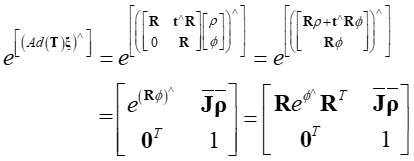
其中,

于是等式右边化简为,
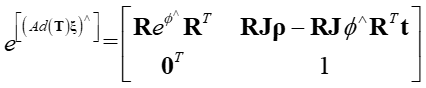
Step4 比较等式左右两边

7、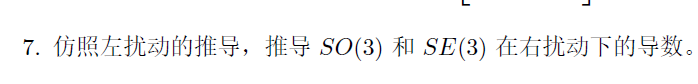
(1)SO(3)

其中隐含了扰动是小量,在进行指数映射忽略了二阶小量,可以回到定义式,一目了然。
(2)SE(3)

8、cmake的find_package()指令
可参考博文:: Cmake语句find_package()函数.
