埃式筛法详解

这个算法简单，也很好理解。通常用于需一次性求解判断大量数是否为质数的问题，我们可以利用埃式筛法打好素数表即可。

埃拉托斯特尼筛法，简称埃氏筛或爱氏筛，是一种由希腊数学家埃拉托斯特尼所提出的一种简单检定素数的算法。要得到自然数n以内的全部素数，必须把不大于√n的所有素数的倍数剔除，剩下的就是素数。

我们这是还是再介绍一下，因为待会我们的埃式筛法就是利用了素数的特点。素数，也被称为质数。若一个数它的除数只有1和它的本身，则就是素数，特别的，1既不是质数，也不是合数。

那么，我们开始！

第一步、假设：对于自然数n以内的数，我们先假定除1以外的数全部为素数。

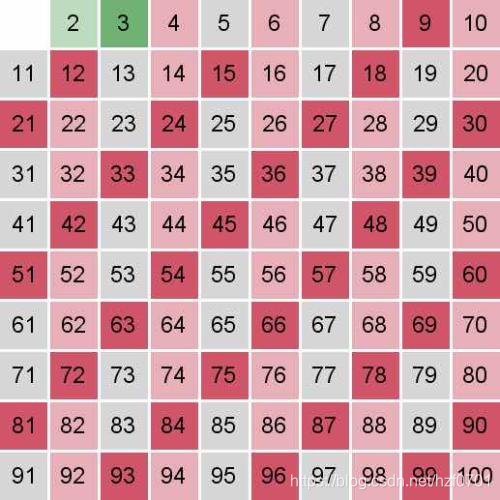
第二步、剔除：怎么剔除？我们要遍历不大于√n的所有素数，再将其素数的倍数都剔除。也许你就会有疑问了，我都还没开始判断是素数，你怎么知道根号n的所有素数呢，别急，有趣的来了，对于2，我们之前就是1，没有其他约数，显然就是素数，那么我们之前的假设成立，OK！剔除2的倍数，==剔除即是解除假定，即不是素数了。==那么我们往下寻找，发现了3没有被剔除，即显然是素数，OK！剔除3的倍数。再往下寻找没有被剔除的数，再剔除该数的倍数。重复完上述步骤后我们看我们筛好的n以内的数。（此处只展示部分。）显然，还没有被剔除的自然都是素数。

那么，还有一个细节，就是我们只需要遍历从不大于√n的素数，读者可以思考一下，这是为什么呢？

我们看，对于根号n以上的素数，我们知道：
从(√n+1)*2到(√n+1)*√n的数，他们是都有一个小于√等于n的约数，则意味着它们这些数在我们遍历不大于√n的素数的时候都已经被剔除了，已经无需再往下去寻找剔除了，减少了时间复杂度。在大于√n的数，没被剔除的自然都是素数了。

这就是埃式筛法的整个过程，那么我们就来编写代码实现吧。

1、基本数据

const int maxn=1000;//需要寻找最大为maxn一下的素数
bool primer[maxn];  //素数表

2、打表函数

void isprimer()  //打好素数表。
{
	int k=sqrt(maxn);
	memset(primer,true,sizeof(primer));//假设全部都是素数。
	primer[0]=primer[1]=false;//0和1自然都不是素数，我们直接剔除（因为根据倍数无法剔除，这些是特殊的）
	for(int i=2;i<=k;i++)
	{
		if(primer[i])//如果i是素数，则剔除它的倍数。
		{
			for(int j=i+i;j<=maxn;j+=i)//遍历i的倍数
				primer[j]=false;//剔除
		}
	}
}

我们看测试结果：

这就是完整的步骤，算法很简短，对于多个测试用例的时候如果我们在输入数据前已经打好了一个素数表，那问题岂不是迎刃而解，直接根据if(primer[t])来判断。大大减少了时间复杂度。这个算法的时间复杂度则是O(√n*logn)。

我们还可以再优化一下，对于剔除的起始位置是2i，而i是大于等于2的，在之后j一直递增i的时候也就是会到ii，在2到i的过程中，存在着2到i的约数，则存在着这些数显然已经被剔除，我们无需再判断剔除了，所以我们的剔除的起始位置可以改为i*i，我们的算法又进一步得到优化。

终极版

void isprimer()  //打好素数表。
{
	int k=sqrt(maxn);
	memset(primer,true,sizeof(primer));//假设全部都是素数。
	primer[0]=primer[1]=false;//0和1自然都不是素数，我们直接剔除（因为根据倍数无法剔除，这些是特殊的）
	for(int i=2;i<=k;i++)
	{
		if(primer[i])//如果i是素数，则剔除它的倍数。
		{
			for(int j=i*i;j<=maxn;j+=i)//遍历i的倍数
				primer[j]=false;//剔除
		}
	}
}

结果没有问题。
终极版的时间复杂度是O(√n*log log n)的，比市面上的埃式筛法的O(n*logn)快了很多倍。