生成树

已知无向连通图 $G$，图上有 $n$个顶点。生成树是指图 $G$的一个极小（边最少）连通子图，生成树上有 $n$个顶点、 $n - 1$条边，且任意两点之间都是连通的。

最小生成树

已知无向带权连通图 $G$，图中有 $n$个顶点，每条边都有权值。我们要从图中抽出一棵生成树，使得树上所有边权之和最小，这棵生成树就叫做最小生成树（Minimum Spanning Tree, MST）。

Kruskal 算法

算法过程

首先按照边权从小到大排序，接着遍历每一条边，如果这条边连接的两点不在同一个连通块，就连接这条边，否则不进行操作

因为要用到判连通和合并操作，所以会使用到并查集

算法演示

第一步：将所有的边按边权从小到大排序。排序完成后，我们选择权值最小的边 $<J, N>$。这样我们的图就变成了：

第二步，在剩下的边中寻找权值最小的边 $<U, X>$：

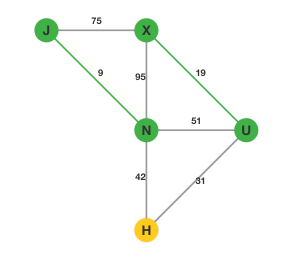
依次类推我们找到 $<H, U>$，图变成：

最后我们只需要再选择 $<H, N>$：

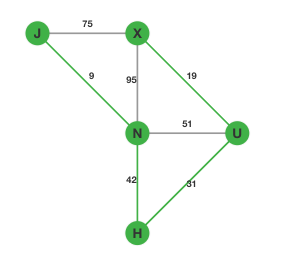
至此所有的点都已经连通，一个最小生成树构建完成。

Kruskal 算法的时间复杂度由排序算法决定，若采用快排则时间复杂度为 $\mathcal{O}(M\log M)$。

总的时间复杂度为 $\mathcal{O}(M \log M + N\alpha (N))$，其中 $\alpha(N)$ 可以近似地被当做常数。

代码实现

极其简单

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN=305;
const int MAXM=305; 
struct edge{
	int u,v,w;
}G[MAXM];
int fa[MAXN];
int get(int x){
	if(fa[x]==x){
		return x;
	}
	return fa[x]=get(fa[x]);
}
bool cmp(edge x,edge y){
	return x.w<y.w;
}
int kruskal(int n,int m){
    int sum=0;
    sort(G+1,G+1+m,cmp);
    for(int i=1;i<=m;i++){
        int fu=get(G[i].u);
        int fv=get(G[i].v);
        if(fu!=fv){
            fa[fv]=fu;
            sum+=G[i].w;
        }
    }
    return sum;
}
int main(){ 
	int n,m;
	scanf("%d %d",&n,&m); 
	for(int i=1;i<=n;i++){
		fa[i]=i;
	}
	for(int i=1;i<=m;i++){
		scanf("%d %d %d",&G[i].u,&G[i].v,&G[i].w);
	}
	printf("%d",kruskal(n,m));
return 0;
} 

算法证明

毕竟这是一个贪心，还是给一下证明吧

要证明正确性，个人认为只要证明两点即可

Kruskal算法一定能得到一个生成树

假设得到的不是生成树，那么有如下两种情况

1. 树上有环
2. 不连通

现在我们一一证明

1. 树上有环

   环可以理解成一条链+一条连接链两端的线，不妨设这条链为 $A-...- B$，显然 $A,B$连通,现在我们思考会不会添加 $A- B$这条边,根据加边的原则，当两端点在同一连通块时，不会加边，即不会添加 $A- B$，即不会形成环

2. 不连通
   假设得到的图是不连通的，则至少包含两个独立的的边集，假设其中一个为E，则E中边对应的所有点都无法到达其它边集对应的点（否则，根据算法定义，相应的联系边应被加入树中），而这与原图是连通的产生矛盾，所以得到的图是连通的，得证。

Kruskal得到的生成树一定最小

根据算法定义，权值最小的边连接的两点一定会被选，那么现在他们已经被选，我们可以对他们进行缩点，由于最小生成树的性质（只要有路径连接两个任意结点即可），缩点对建图没有任何影响。
不断重复以上过程，每次选择的都是当前最小权值，结果也一定是最小的，得证

综上，Kruskal算法一定可以得到最小生成树