最近在读《Introduction to Data Mining 》这本书，发现课后答案只有英文版，于是打算结合自己的理解将答案翻译一下，其中难免有错误，欢迎大家指正和讨论。侵删。

第九章

考虑文档数据，如果两个文档是相似的那么它们包含很多相同的词，并且没出现的词在大部分情况下都是无意义的。当一个文档中的词频繁出现，那么这个词在相似性度量上会占比较大的比重。举例来说，如果一个词有多个意思，那么可能会得出错误的结论，比如词“game”，在讨论“sports game”和“video game”两篇文章中是不相似的。

O(m²)

文档向量规范化后，是在一个n维球形空间中。这个簇是一个类似圆锥体的形状，它与球形空间的交点在球形空间的表面是一个圆。

优点：能更好地定义和解释在聚类问题中的处理过程；可以利用已经比较成熟的最优化理论和技术。
缺点：最优化算法大部分时间复杂度都比较高，而且存在NP-hard问题，这时就需要用启发式算法退而求其次，找出局部最优解，但随着而来的问题就是解的结果可能不一样。另一个问题就是约束条件更加支持大的簇而不是小的簇。

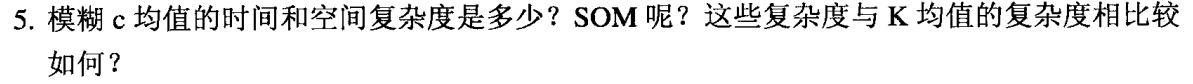
K均值时间复杂度为O（mnK*I)，其中m是点的个数，n是属性的个数，K是簇的个数，I是收敛所需迭代次数。模糊c均值、SOM的时间复杂度都和K均值的一样。但由于SOM的质心需要一直更新，因此实际运行起来SOM会比较慢一点。

c均值和K均值有同样的能力，在处理这些问题上比较吃力，c均值对比K均值唯一的优点就是在指派点属于哪个簇并不困难。

优点：当处理一个不强属于任何簇的离群点时，这个点会有很低的隶属度。
缺点：当簇划分不明确的时候初始化很难，比如几个簇的中心可能融在一起时，或当簇中心在迭代过程中变化时。

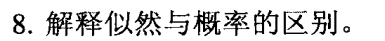
举个例子来说明
概率：如果我有一枚质地均匀的硬币，那么它出现正面朝上的概率是0.5
似然：如果抛一枚硬币100次，正面朝上的次数是50次，那么这枚硬币很有可能是质地均匀的。



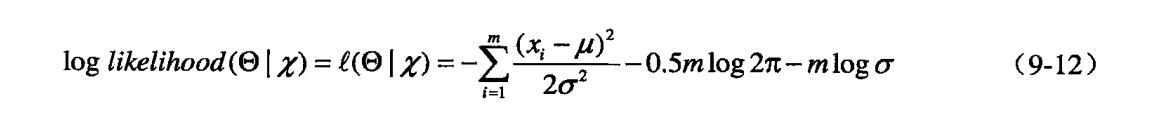
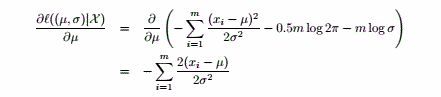
令上式=0，得


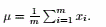
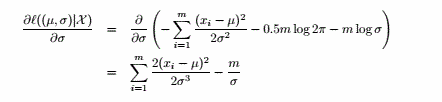
令上式=0，得


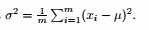
男人和女人身高服从高斯分布，但均值不同且很可能方差也不同。所以考虑用混合模型，包含这四个参数，如果样本够大，可以足够逼近。



模糊c均值聚类仅仅给那些靠近簇中心的点分配高权值，而对边缘点分配低权值。但远离簇中心的点的权值比那些处于簇交界地带的点的权值高。
而EM聚类对簇中心点和簇边界点都分配了高权值，处于簇交界地带的点的权值稍低，但没有模糊c均值中那么低。
这两个算法的主要区别就是对于那些处于交界地带的点，模糊c均值算法中会将这种点隶属于各个簇的权值分配的比较平均，而EM算法会表明这种点强属于哪一个簇。


在EM聚类中，我们计算一个点隶属于一个簇的概率值。这个概率值既取决于点离簇中心的距离，也取决于簇的分散程度。因此，在上图中，左边的簇很分散，而右边的簇非常紧凑，因此用箭头指出的点属于左边的簇是可能的。但在K均值聚类中，只考虑到最近簇的距离，用箭头指出的点属于左边的簇是不可能的。

（a）举个简单的例子： b ac，a在b的最近邻中，但a的最近邻是c。
（b）如果第i行第j列的元素是0就将第j行第i列也设置为0；另一种办法就是如果第i行第j列的元素是1就将第j行第i列也设置为1.

定义：

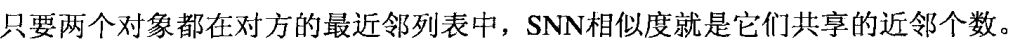
答：


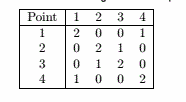
（a）基于最近邻点的位置赋予权值即可。
（b）缺点：复杂度大大提高。优点：更加合理，原来的定义会有很多SSN值相同的点，修改定义后可以将原SSN相同的点做进一步的排序，而且可能对k的选取有帮助。

当需要基于绝对距离或绝对密度聚类时。


（a）
在网格聚类中，对于结果簇的描述是基于空间的划分而不是点的集合。对于如果不是矩形的簇只能给出大概的形状。
（b）
基于网格聚类是典型的只关注稠密区域的方法。因此对于稀疏的数据不是很适合

的确是一个问题。并且类似的问题在关联分析中同样存在，有很多项的关联模式的支持度一般都比较低，这样的情况下用Apriori算法会很困难，如果降低支持度阈值会带来很多项不多的关联模式。一个解决办法就是随着维数增加而降低阈值。

Charles Elkan 提出了下述定理：
设x是任一个点，设b和c是簇的中心点。
如果d(b,c) ≥ 2d(x,b) ，那么 d(x,c) ≥ d(x,b).
证明：由d(b,c) ≤ d(b,x) + d(x,c)
得d(b,c) - d(x,b) ≤ d(x,c)
又d(b,c) - d(x,b) ≥ 2d(x,b) - d(x,b) = d(x,b)
因此d(x,b) ≤ d(x,c)
这个定理可以减少很多计算。

概率分别为0、0、0.54