Fibonacci Sum

Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)
Total Submission(s): 2930 Accepted Submission(s): 643

Problem Description

The Fibonacci numbers are defined as below:

Given three integers N, C and K, calculate the following summation:

Since the answer can be huge, output it modulo 1000000009 (109+9).

Input

The first line contains an integer T (1≤T≤200), denoting the number of test cases. Each test case contains three space separated integers in the order: N, C, K (1≤N,C≤1018,1≤K≤105).

Output

For each test case, output a single line containing the answer.

Sample Input

2 5 1 1 2 1 2

Sample Output

12 2

Source

2020 Multi-University Training Contest 1

Recommend

liuyiding

题意:

即求上式。

思路:

斐波那契的通项公式：

$F_{n}=\frac{\sqrt{5}}{5}*((\frac{1 + \sqrt{5}}{2})^{n}-(\frac{1 - \sqrt{5}}{2})^{n})$

先考虑如何求

$ans=F_{1}^{m}+F_{2}^{m}+...+F_{n}^{m}$

设

$S=\frac{\sqrt{5}}{5}\\R1 = (\frac{1 + \sqrt{5}}{2})^{n}\\R2=(\frac{1 - \sqrt{5}}{2})^{n}$

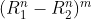$ans_{n}=S^{m}*(R_{1}^{n}-R_{2}^{n})^{m}$

将 $(R_{1}^{n}-R_{2}^{n})^{m}$ 二项式展开，可得到总和：

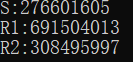
$ans=\sum_{i=1}^{n}\sum_{k=0}^{m}C_{m}^{k}*(R_{1}^{n})^{k}*(R_{2}^{n})^{m-k}*(-1)^{m-k}\\=\sum_{k=0}^{m}C_{m}^{k}*\sum_{i=1}^{n}R_{1}^{i*k}*R_{2}^{i*(m-k)}*(-1)^{m-k}$

通过下面的BF算法求二次剩余代码可以算出根号五在模1e9+9意义下的值。

	for (ll i = 1;; i++)
	{
		if (i * i % mod == 5)
		{
			cout << "S:"<<fpow(i, mod - 2) << endl;
			cout << "R1:" << (i + 1) * fpow(2, mod - 2) % mod << endl;
			cout << "R2:" << (1 - i + mod) % mod * fpow(2, mod - 2) % mod << endl;
			break;
		}
	}

枚举k，然后，中间一部分用等比数列求和公式即可。

对于这道题跳着C个一选，即公比发生了改变，直接求即可，就是有点卡常，需要注意下等比数列求和优化。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
const int mod = 1e9 + 9;
const int MOD = 1e9 + 8;
typedef long long ll;
#ifdef LOCAL
#define TIME cout << "RuningTime: " << clock() << "ms\n", 0
#else
#define TIME 0
#endif
ll s = 276601605;
ll r1 = 691504013;
ll r2 = 308495997;
ll jc[N];
ll R1[N];
ll R2[N];
ll inv[N];
ll g[N];
ll fpow(ll a, ll b)
{
    ll res = 1;
    while (b)
    {
        if (b & 1)
            res = res * a % mod;
        b >>= 1;
        a = a * a % mod;
    }
    return res;
}
ll calc1(ll a, ll b)
{
    return jc[a] * inv[b] % mod * inv[a - b] % mod;
}
void init()
{
    jc[0] = R1[0] = R2[0] = 1;
    for (int i = 1; i <= 100000; i++)
        jc[i] = jc[i - 1] * i % mod;
    inv[100000] = fpow(jc[100000], mod - 2);
    for (int i = 99999; i >= 0; i--)
        inv[i] = inv[i + 1] * (i + 1) % mod; 
}
ll calc2(ll q, ll n, ll g)//等比数列求和 
{
    if (q == 1)
        return n % mod;
    ll u = (1 - q + mod) % mod;
    return (1 - g + mod) % mod * fpow(u, mod - 2) % mod; 
}
int main()
{
#ifdef LOCAL
    freopen("E:\\input.txt", "r", stdin);
#endif
    init();
    int t;
    cin >> t;
    while (t--)
    {
        ll n, k, c;
        scanf("%lld%lld%lld", &n, &c, &k);
        c %= MOD;
        ll sum = 0; 
        ll RR1 = fpow (r1, c);
        ll RR2 = fpow(fpow(r2, c), mod - 2);
        ll RRR1 = fpow(RR1, (n + 1) % MOD);
        ll RRR2 = fpow(RR2, (n + 1) % MOD);
        ll y = fpow(fpow(r2, k), c); //公比
        ll g = fpow(y, (n + 1) % MOD); //公比的(n+1)次方
        for (int i = 0; i <= k; i++)
        {    
            ll now = calc1(k, i) * calc2(y, n + 1, g) % mod; //首项F0是1就不用管了。
            if ((k - i) % 2 != 0)
                now = -now;
            if (now < 0)
                now += mod;
            sum = sum + now;
            if (sum > mod)
                sum %= mod;
            y = y * RR1 % mod * RR2 % mod;
            g = g * RRR1 % mod * RRR2 % mod;
        } 
        printf("%lld\n", sum * fpow(s, k) % mod);
    }
    return TIME;
}

2020 Multi-University Training Contest 1 Fibonacci Sum(二次剩余，二项式定理)

Fibonacci Sum

题意:

思路:

猜你喜欢