通俗理解线性回归
回归分析
什么是回归分析呢?这是一个来自统计学的概念。回归分析是指一种预测性的建模技术,主要是研究自变量和因变量的关系。通常使用线/曲线来拟合数据点,然后研究如何使曲线到数据点的距离差异最小。
例如,存在以下数据

然后我们拟合一条曲线f(x):

回归分析的目标就是要拟合一条曲线,让图中红色线段加起来的和最小。
线性回归(简介)
线性回归是回归分析的一种。
- 假设目标值(因变量)与特征值(自变量)之间线性相关(即满足一个多元一次方程,如:f(x)=w1x1+…+wnxn+b.)。
- 然后构建损失函数。
- 最后通过令损失函数最小来确定参数。(最关键的一步)
线性回归(详解)
还是按照简介的思路来说,以简单的一元线性回归(一元代表只有一个未知自变量)做介绍。
有n组数据,自变量x(x1,x2,…,xn),因变量y(y1,y2,…,yn),然后我们假设它们之间的关系是:f(x)=ax+b。那么线性回归的目标就是如何让f(x)和y之间的差异最小,换句话说就是a,b取什么值的时候f(x)和y最接近。
这里我们得先解决另一个问题,就是如何衡量f(x)和y之间的差异。在回归问题中,均方误差是回归任务中最常用的性能度量(自行百度一下均方误差)。记J(a,b)为f(x)和y之间的差异,即
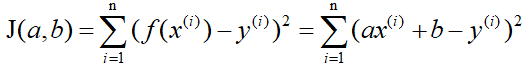
i代表n组数据中的第i组。
这里称J(a,b)为损失函数,明显可以看出它是个二次函数,即凸函数(这里的凸函数对应中文教材的凹函数),所以有最小值。当J(a,b)取最小值的时候,f(x)和y的差异最小,然后我们可以通过J(a,b)取最小值来确定a和b的值。
到这里可以说线性回归就这些了,只不过我们还需要解决其中最关键的问题:确定a和b的值。
下面介绍三种方法来确定a和b的值:
- 最小二乘法
既然损失函数J(a,b)是凸函数,那么分别关于a和b对J(a,b)求偏导,并令其为零解出a和b。这里直接给出结果:


解得:
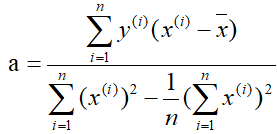
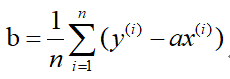
-
梯度下降法
首先你得先了解一下梯度的概念:梯度的本意是一个向量(矢量),表示某一函数(该函数一般是二元及以上的)在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
当函数是一元函数时,梯度就是导数。这里我们用一个最简单的例子来讲解梯度下降法,然后推广理解更为复杂的函数。
还是用上面的例子,有n组数据,自变量x(x1,x2,…,xn),因变量y(y1,y2,…,yn),但这次我们假设它们之间的关系是:f(x)=ax。记J(a)为f(x)和y之间的差异,即
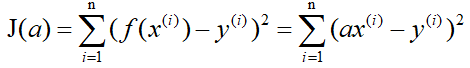
在梯度下降法中,需要我们先给参数a赋一个预设值,然后再一点一点的修改a,直到J(a)取最小值时,确定a的值。下面直接给出梯度下降法的公式(其中α为正数):

下面解释一下公式的意义,J(a)和a的关系如下图,
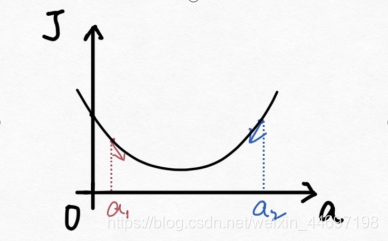
假设给a取的预设值是a1的话,那么a对J(a)的导数为负数,则
也为负数,所以

意味着a向右移一点。然后重复这个动作,直到J(a)到达最小值。
同理,假设给a取的预设值是a2的话,那么a对J(a)的导数为正数,则

意味着a向左移一点。然后重复这个动作,直到J(a)到达最小值。
所以我们可以看到,不管a的预设值取多少,J(a)经过梯度下降法的多次重复后,最后总能到达最小值。
这里再举个生活中的栗子,梯度下降法中随机给a赋一个预设值就好比你随机出现在一个山坡上,然后这时候你想以最快的方式走到山谷的最低点,那么你就得判断你的下一步该往那边走,走完一步之后同样再次判断下一步的方向,以此类推就能走到山谷的最低点了。而公式中的α我们称它为学习率,在栗子中可以理解为你每一步跨出去的步伐有多大,α越大,步伐就越大。(实际中α的取值不能太大也不能太小,太大会造成损失函数J接近最小值时,下一步就越过去了。好比在你接近山谷的最低点时,你步伐太大一步跨过去了,下一步往回走的时候又是如此跨过去,永远到达不了最低点;α太小又会造成移动速度太慢,因为我们当然希望在能确保走到最低点的前提下越快越好。)
到这里,梯度下降法的思想你基本就理解了,只不过在栗子中我们是用最简单的情况来说明,而事实上梯度下降法可以推广到多元线性函数上,这里直接给出公式,理解上(需要你对多元函数的相关知识有了解)和上面的栗子殊途同归。
假设有n组数据,其中目标值(因变量)与特征值(自变量)之间的关系为:
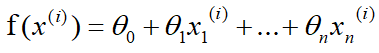
其中i表示第i组数据,损失函数为:
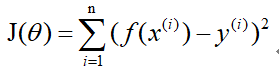
梯度下降法:
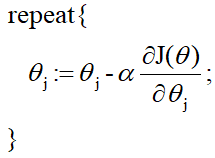
-
正规方程
(这里需要用到矩阵的知识)
正规方程一般用在多元线性回归中,原因等你看完也就能理解为什么。所以这里不再用一元线性回归举栗子了。
同样,假设有n组数据,其中目标值(因变量)与特征值(自变量)之间的关系为:
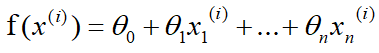
其中i表示第i组数据,这里先直接给出正规方程的公式: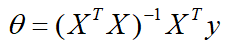
推导过程如下:
记矩阵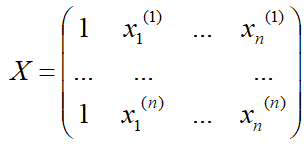
向量
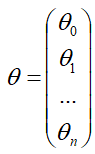

则
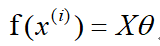
损失函数为: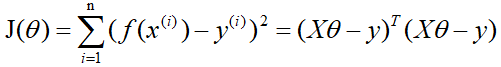
对损失函数求导并令其为0,有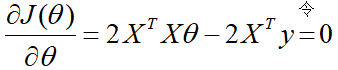
解得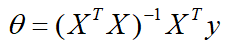
到此,就求出了所有系数θ。不过正规方程需要注意的是
在实际中可能会出现是奇异矩阵,往往是因为特征值之间不独立。这时候需要对特征值进行筛选,剔除那些存在线性关系的特征值(好比在预测房价中,特征值1代表以英尺为尺寸计算房子,特征值2代表以平方米为尺寸计算房子,这时特征值1和特征值2只需要留1个即可)。
好了,以上就是线性回归的讲解(如果对你理解线性回归确实有帮助的话,帮忙点个赞,同时也欢迎指出问题)。 下面再补充一下个人对上面三种确定系数θ方法的评估。
- 梯度下降法是通用的,包括更为复杂的逻辑回归算法中也可以使用,但是对于较小的数据量来说它的速度并没有优势
- 正规方程的速度往往更快,但是当数量级达到一定的时候,还是梯度下降法更快,因为正规方程中需要对矩阵求逆,而求逆的时间复杂的是n的3次方
- 最小二乘法一般比较少用,虽然它的思想比较简单,在计算过程中需要对损失函数求导并令其为0,从而解出系数θ。但是对于计算机来说很难实现,所以一般不使用最小二乘法。