本文档支持 Markdown,需要源代码的请与我联系,我多半是不会给的。
计算几何是一个庞大的模块,因此需要这么一个学习笔记记录各个知识点。
模块 1 线性的几何
1. dcmp 比较函数 以及 Point(Vector)的定义
由于浮点数有精度问题,因此比较时一定要使用 dcmp 而不是 ==。
Vector 在类型上和 Point 是一样的,这会在代码量上带来方便,但是无法阻止不经意的“点 + 点”之类的操作。
INT dcmp(const double x)
{
const double EPS = 1e-10;
if (std::abs(x) <= EPS) return 0;
return x < 0 ? -1 : 1;
}
struct Point
{
double x, y;
Point() {}
Point(const double& x, const double& y) : x(x), y(y) {}
bool operator==(const Point& b) const { return !dcmp(x - b.x) && !dcmp(x - b.x); }
};
typedef Point Vector;2. 向量的加减,数乘
注意对点进行向量减法时起点和终点的一一对应。
//由于数据类型实质相同,因此需要手动对号入座
Vector operator+(const Vector& a, const Vector& b)
{
return Vector(a.x + b.x, a.y + b.y);
}
//A - B,在坐标表示上是 a.x - b.x, a.y - b.y
//对于点而言,A是终点,B是起点
Vector operator-(const Vector& a, const Vector& b)
{
return Vector(a.x - b.x, a.y - b.y);
}
Vector operator*(const Vector& a, const double& b)
{
return Vector(a.x * b, a.y * b);
}
Vector operator/(const Vector& a, const double& b)
{
return Vector(a.x / b, a.y / b);
}3. 向量的点积和叉积以及其最简单的应用
这个没什么好讲的。注意叉积不满足交换律。
特别强调:所有系统数学函数均在 std 命名空间中,这很重要,因为只有在此命名空间中 abs 等函数才是模板函数!
//点积
double Dot(const Vector& a, const Vector& b)
{
return a.x * b.x + a.y * b.y;
}
//叉积
double Cross(const Vector& a, const Vector& b)
{
return a.x * b.y - b.x * a.y;
}
//使用点积计算长度
double Length(const Vector& a)
{
return std::sqrt(Dot(a, a));
}
//使用 a * b = |a||b| cos<a, b> 计算夹角
double Angle(const Vector& a, const Vector& b)
{
return std::acos(Dot(a, b) / Length(a) / Length(b));
}
//求单位向量
Vector Unit(const Vector& a)
{
double length = Length(a);
return Vector(a.x / length, a.y / length);
}4. 向量的旋转
//使用三角函数推导向量旋转
//x0 = L * cos(A)
//y0 = L * sin(A)
//x1 = L * cos(A + B) = L * (cosAcosB - sinAsinB)
//y1 = L * sin(A + B) = L * (sinAcosB + cosAsinB)
//B 为旋转角
//cos(A) = x0 / L
//sin(A) = y0 / L
//代入 cosA, sinA 即为答案
//记忆方法:
//x y,y x,x1 的系数为 cos(A + B) 的 B 的三角函数,y1 的系数为 sin(A + B) 的 B 的三角函数
//x * cosB - y * sinB, y * cosB + x * sinB
Vector Rotate(const Vector& a, const double& rad)
{
return Vector(a.x * std::cos(rad) - a.y * std::sin(rad), a.y * std::cos(rad) + a.x * std::sin(rad));
}
//特殊角:
//逆时针旋转 π / 4:-y, x
//顺时针旋转 π / 4:y, -x5. 直线的定义
直线使用参数表示法,用一个点,一个向量和一个参量(向量的系数)表示直线。
struct Line
{
Point p;
Vector v;
Line() {}
Line(const Point& p, const Vector& v) : p(p), v(v) {}
Point point(const double& t) const
{
return p + v * t;
}
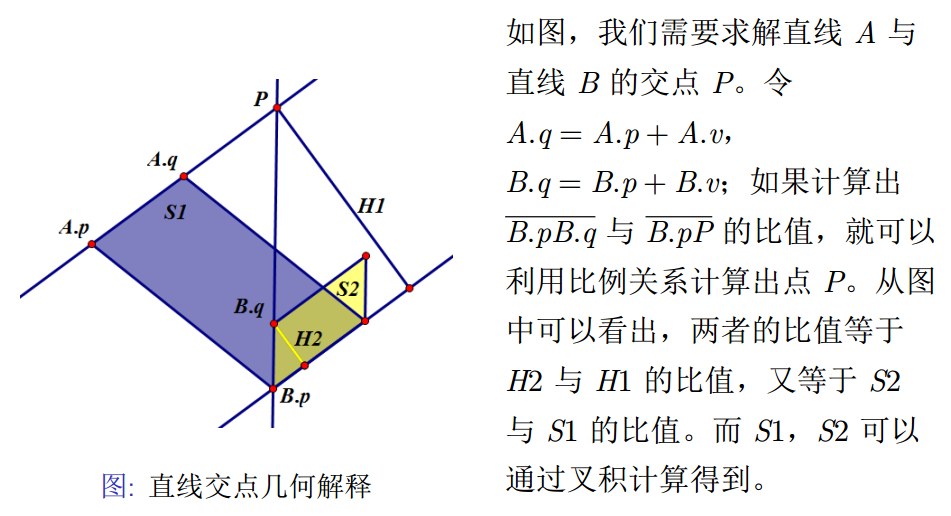
};6. 给定直线求直线的交点
在给出此图后,只贴个代码:
//取两直线交点,当且仅当 a × b != 0 时两直线有交点
//作图,不难发现当代码右边那两个叉积之商应该为正时,u 和 b.v 的左右应相同,这样就能推导出 u = a.p - b.p 而不是其相反向量了(注意起点和终点谁是谁)
Point GetLinesIntersection(const Line& a, const Line& b)
{
Vector u = a.p - b.p;
return b.p + b.v * (Cross(a.v, u) / Cross(a.v, b.v));
}7. 求点到直线的距离
用叉乘算出平行四边形的面积后,除以底边得到高,高就是点到直线的距离,注意要加绝对值。
//求点到直线的距离,使用叉乘
double DistanceFromPointToLine(const Point& a, const Line& b)
{
return std::abs(Cross(a - b.p, b.v) / Length(b.v));
}8. 线段的定义
往往使用线段的两个端点表示线段。
注意新的语法内容:重载类型转换符。
struct Segment
{
Point u, v;
Segment() {}
Segment(const Point& u, const Point& v) : u(u), v(v) {}
double Length() const
{
return ComputationGeometry::Length(u - v);
}
operator Vector() const
{
return v - u;
}
};9. 点到线段的距离
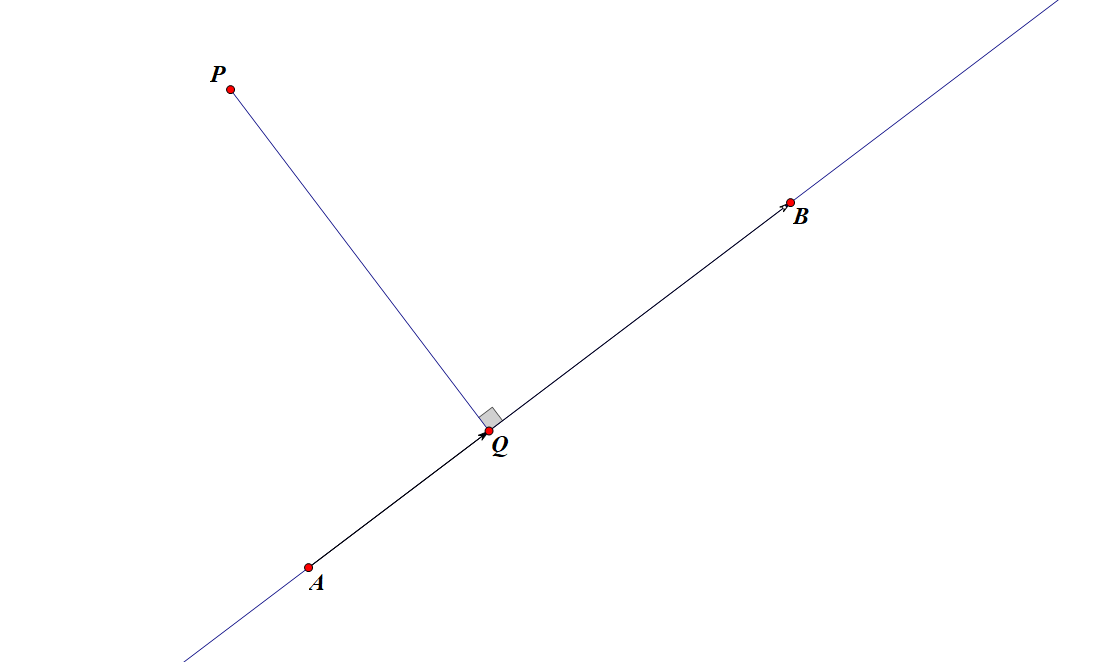
当点 P 在线段 AB 所在直线的投影点 Q 在线段上时,则所求距离就是 PQ 的长度。
如果 Q 在射线 BA 上,所求距离为 PA 的长度,否则所求距离为 PB 的长度。
当 Q 在线段 AB 上时,∠PAB 和 ∠PBA 均为锐角或直角;当 ∠PAB 为钝角时,Q 在射线 BA 上;当 ∠PBA 为钝角时,Q 在射线 AB 上。
使用点积判断即可。
//点到线段的距离
double DistanceFromPointToSegment(const Point& a, const Segment& b)
{
if (b.u == b.v) return Length(a - b.u);
Vector UA = a - b.u;
Vector VA = a - b.v;
Vector UV = b.v - b.u;
if (dcmp(Dot(UA, UV)) < 0)
return Length(UA);
else if (dcmp(Dot(VA, UV)) > 0) //VA * VU < 0
return Length(VA);
else
return std::abs(Cross(UA, UV) / b.Length());
}10. 点在直线上的投影
可以用待定系数法。设直线 AB 为参数式 A + tv,设 Q 的参数为 。根据垂直,PQ 和 AB 的点积应为 0。
//点在直线上的投影
Point GetLineProjection(const Point& a, const Line& b)
{
return b.p + b.v * (Dot(a - b.p, b.v) / Dot(b.v, b.v));
}11. 线段规范相交判定
线段的规范相交指:两线段恰好有一个公共点,且不在任何一条线段的端点。线段规范相交的充分必要条件是:每条线段的两个端点都在另一条线段的两侧。使用叉积实现。
//判断线段是否规范相交
bool IsSegmentsProperIntersection(const Segment& a, const Segment& b)
{
if (dcmp(Cross(a, a.u - b.u)) * dcmp(Cross(a, a.u - b.v)) >= 0) return false;
if (dcmp(Cross(b, b.u - a.u)) * dcmp(Cross(b, b.u - a.v)) >= 0) return false;
return true;
}12. 判断线段相交
首先需要一个判断点是否在线段上的函数。
可以用叉积判断点是否在线段所在直线上(叉积为 0),再用点积判断点是否在线段上(点积小于(等于))。若点在线段的端点上也算在线段上,则点积小于等于 0 就返回真,否则仅当在点积小于 0 时才返回真。
//判断点是否在线段上
bool IsOnSegment(const Point& a, const Segment& b)
{
return dcmp(Cross(a - b.u, a - b.v)) == 0 && dcmp(Dot(a - b.u, a - b.v)) <= 0;
} 若两线段共线,即 dcmp(Cross(a, a.u - b.u)) dcmp(Cross(a, a.u - b.v)) 均为 0 时,则至少有一个(端)点在另一条线段上时两线段相交。否则直接把规范相交中的小于号(上面的代码是取反了的符号)换成小于等于号。
//判断线段是否相交
bool IsSegmentsIntersection(const Segment& a, const Segment& b)
{
double c1 = Cross(a, a.u - b.u);
double c2 = Cross(a, a.u - b.v);
if (!dcmp(c1) && !dcmp(c2))
return IsOnSegment(a.u, b) || IsOnSegment(a.v, b) || IsOnSegment(b.u, a) || IsOnSegment(b.v, a);
double c3 = Cross(b, b.u - a.u);
double c4 = Cross(b, b.u - a.v);
return dcmp(c1) * dcmp(c2) <= 0 && dcmp(c3) * dcmp(c4) <= 0;
}13. 求多边形面积
将点的坐标按顺时针方向排序后(即能一笔画的方向),以 p[0] 为向量起点,p[i] 和 p[i +1] 为向量终点,求叉积的和。最终的和即为面积的两倍。由于这个东西过于简单(其实是因为我懒),所以就不贴解析和代码了,可以自己看看书,百度一下。
注意,若点的坐标是按逆时针方向给出的,则求出的面积是一个负数(因为是有向面积,这也是这个算法能求任意多边形的面积的原因),为了保险,可以给答案加一个绝对值。
模块 2 圆
1.圆的定义
用圆心坐标和半径长度表示圆。
可以用 point 函数求出圆上任意一点,这个可以由三角函数的定义实现。
//应该在草稿纸上推导出计算方法后再照着推导结果打出代码
struct Circle
{
Point c;
double r;
Circle() {}
Circle(const Point& c, const double& r) : c(c), r(r) {}
Point point(const double& rad) const
{
return Point(c.x + std::cos(rad) * r, c.y + std::sin(rad) * r);
}
};2. 直线与圆的交点
①解方程组法
设圆 Circle a
设直线 Line b
设交点 P = b.p + t * b.v
则由圆的标准方程:
(P.x - a.c.x) ^ 2 + (P.y - a.c.y) ^ 2 = (a.r) ^ 2
代入得:
(b.p.x + t * b.v.x - a.c.x) ^ 2 + (b.p.y + t * b.v.y - a.c.y) ^ 2 = (a.c.r) ^ 2
设 m = b.v.x,n = b.v.y,p = b.p.x - a.c.x,q = b.p.y - a.c.y,r = a.r(把已知的整理)
有 (t * m + p) ^ 2 + (t * n + q) ^ 2 = r ^ 2
整理为一元二次方程为(这个东西不重要,关键是以上的推导)
(m ^ 2 + n ^ 2) * t ^ 2 + 2 * (m * p + n * q) * t + p ^ 2 + q ^ 2 - r ^ 2 = 0
然后用求根公式。
注意:这个比较贴近于解析几何,所以在草稿纸上(或者在电脑上)算 是最关键的一步!
方法:在推导时随时合并已知项,并在最终代码中体现为定义变量。
//直线和圆的交点(解方程组法)
INT GetLineIntersection(const Circle& a, const Line& b, double& t1, double& t2, Point& p1, Point& p2)
{
double m = b.v.x;
double n = b.v.y;
double p = b.p.x - a.c.x;
double q = b.p.y - a.c.y;
double r = a.r;
double A = (m * m + n * n);
double B = 2 * (m * p + n * q);
double C = p * p + q * q - r * r;
double delta = B * B - 4 * A * C;
if (dcmp(delta) < 0)
return 0;
else if (dcmp(delta) == 0)
{
p1 = p2 = b.point(t1 = t2 = -B / (2 * A));
return 1;
}
//else
delta = std::sqrt(delta);
p1 = b.point(t1 = (-B - delta) / (2 * A));
p2 = b.point(t2 = (-B + delta) / (2 * A));
return 2;
}②几何法
利用圆中的直角三角形求出 t。
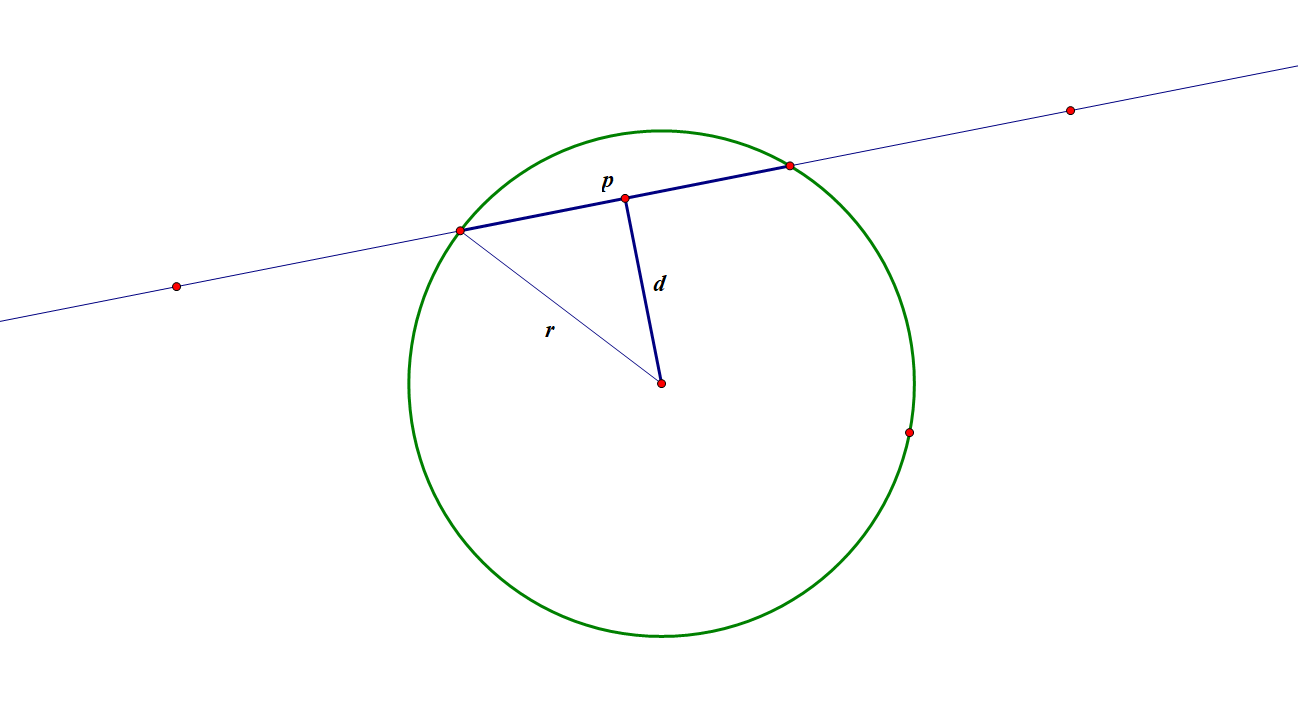
首先求得 a.c 在 b 上的投影 P(a 为圆,b 为直线)。若 P 到 a.c 的距离大于 r,则无交点;若等于 r,则交点为 P(此时 P 为切点);若小于 r,则继续求解。
设 b.v 的单位向量为 v’,则只需要知道 P 到交点的距离 L,就能得到交点为 P ± L * v’,而 L 可以用勾股定理算出。
//直线和圆的交点(几何法)
INT GetLineIntersection(const Circle& a, const Line& b, Point& p1, Point& p2)
{
Point p = GetLineProjection(a.c, b);
double d = Length(p - a.c);
if (dcmp(d - a.r) > 0)
return 0;
else if (dcmp(d - a.r) == 0)
{
p1 = p2 = p;
return 1;
}
//else
Vector v = Unit(b.v);
double L = std::sqrt(a.r * a.r - d * d);
p1 = p - v * L;
p2 = p + v * L;
return 2;
}3. 两圆相交的交点
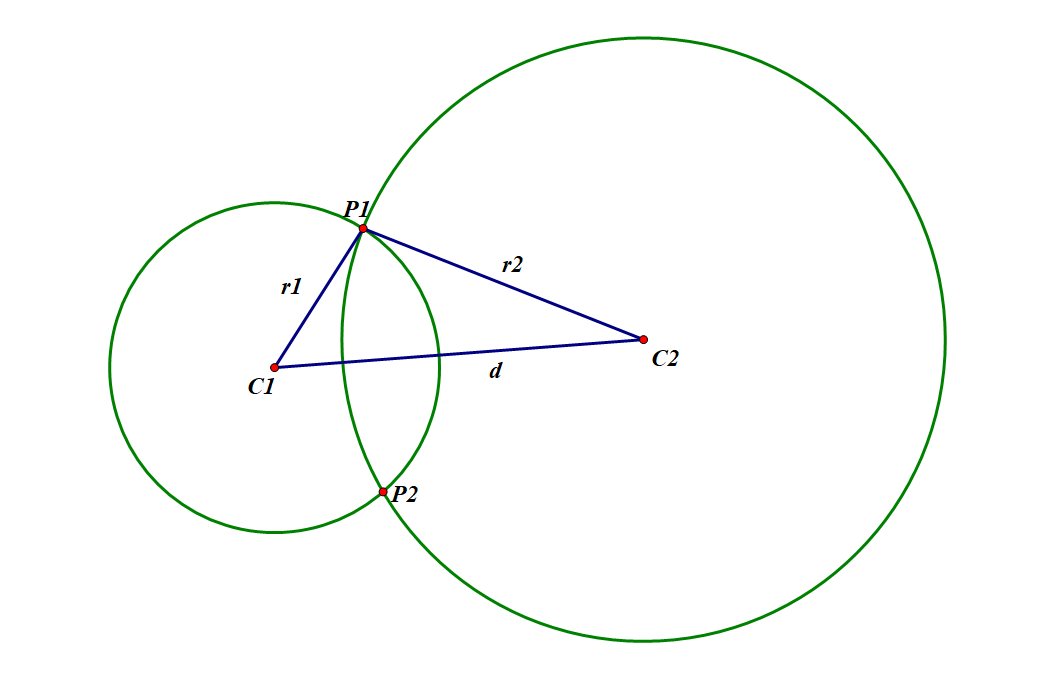
用几何法。
设两圆分别为 a 和 b。可以求出 a.c 到 b.c 的距离 d,当且仅当 abs(a.r - b.r) <= d <= a.r + b.r 时两圆之间有交点。
然后用余弦定理,将问题转换为了求角度。使用 atan2 求向量的极角。知道了角度,又知道了圆,就可以知道圆上一点的坐标了。
//圆与圆的交点(余弦定理)
INT GetCirclesIntersection(const Circle& a, const Circle& b, Point& p1, Point& p2)
{
double d = Length(a.c - b.c);
if (dcmp(d) == 0)
{
if (dcmp(a.r - b.r) == 0)
return -1; //两圆相交
else
return 0;
}
if (dcmp(a.r + b.r - d) < 0)
return 0; //外离
if (dcmp(std::abs(a.r - b.r) - d) > 0)
return 0; //内含
double AngleA = Angle(b.c - a.c); //注意以 a 为中心,则向量起点为 a.c
double AngleDR = std::acos((a.r * a.r + d * d - b.r * b.r) / (2 * a.r * d)); //余弦定理
p1 = a.point(AngleA - AngleDR);
p2 = a.point(AngleA + AngleDR);
return 1 + !(p1 == p2);
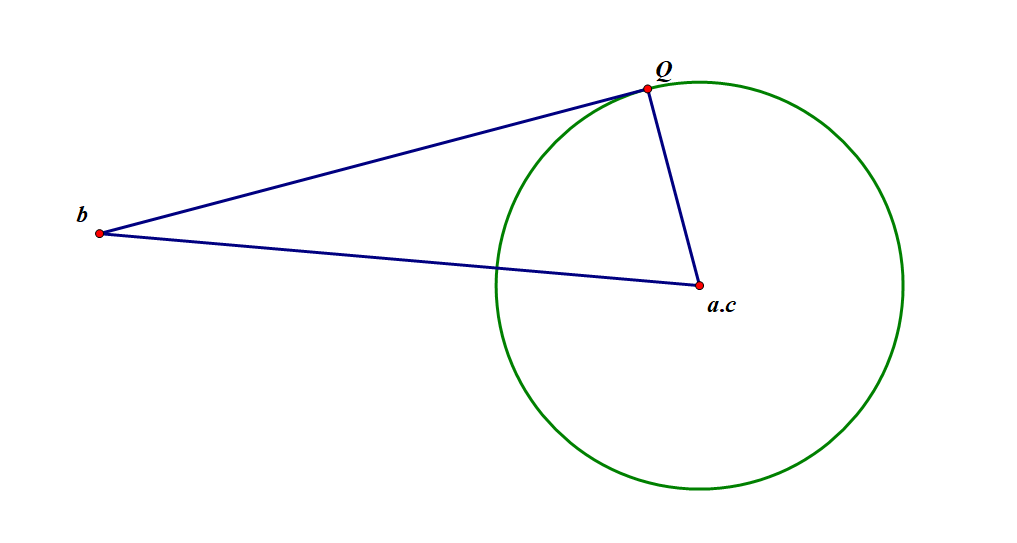
}4. 过定点作圆的切线
设圆为 a,定点为 b,切点为 Q。依然用求角的思想。先求出 a.c 与 b 的距离 d。若 d < r,无解;若 d = r,将向量 b -> a.c 旋转 90 度即可,否则就用反正弦函数得到切线与连线的夹角大小,再旋转向量即可。
//圆的切线
INT GetTangents(const Circle& a, const Point& b, Vector& v1, Vector& v2)
{
Vector u = a.c - b; //起点为 p
double d = Length(u);
if (dcmp(d - a.r) == 0)
{
v1 = v2 = Rotate(u, std::acos(-1) / 2); //旋转 90 度
return 1;
}
else if (dcmp(d - a.r) < 0)
return 0;
double Angle = asin(a.r / d);
v1 = Rotate(u, -Angle);
v2 = Rotate(u, Angle);
return 2;
}5. 两圆的公切线
根据两圆的圆心距从小到大排序,有 6 种情况:
情况一:两圆完全重合,有无数条公切线。
情况二:两圆内含,没有公切线。
情况三:两圆内切,有 1 条外公切线。
情况四:两圆相交,有 2 条外公切线。
情况五:两圆外切,有 3 条公切线,其中 1 条内公切线,2 条外公切线。
情况六:两圆相离,有 4 条公切线,其中 2 条内公切线,2 条外公切线。
通过求圆心距离 d,分情况解决。
情况一,情况二:没有什么好说的。
情况三和情况五的内公切线:这相当于是过圆上一点求圆的切线,只需连接圆心和切线,旋转 90° 后即可知道切线的方向向量。
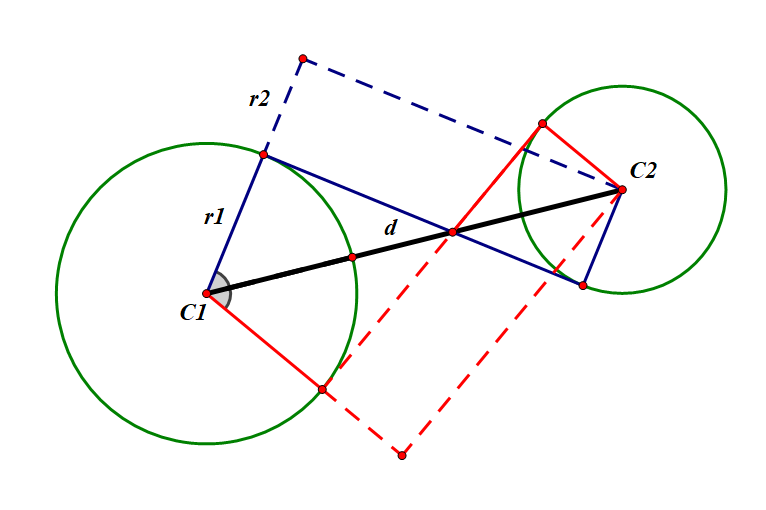
情况六的内公切线(解决掉它后就没有内公切线了):
(图片中 )
首先,假设 ,否则交换两圆。不难得到 ,然后就可以旋转 得到切点了。另一个切点的求法同理,并且由于角度相同(如图),所以不必再求,只需要取相反数即可。
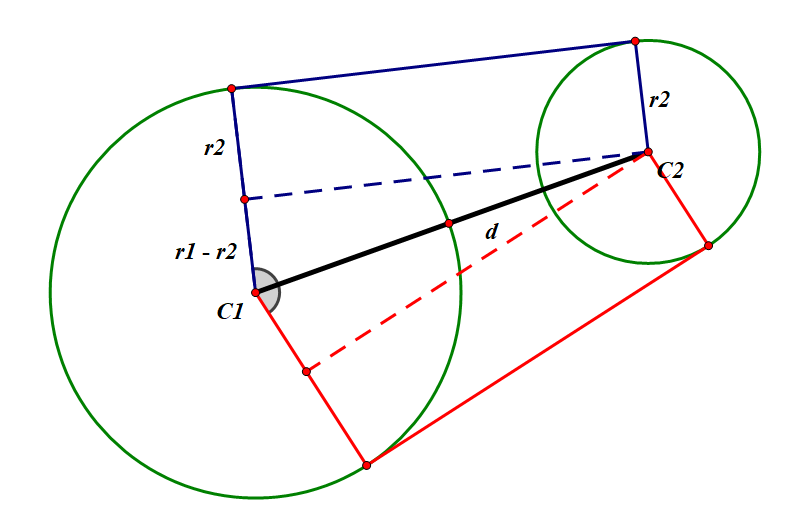
情况四、情况五和情况六的外公切线:
同样假设 。则 ,然后旋转向量得到一个切点。另一个切点仍然满足对称性质,将角度取相反数即可。
//圆的公切线(求切点)
INT GetCommonTangents(const Circle& a, const Circle& b, Point* pa, Point* pb)
{
if (dcmp(a.r - b.r) < 0)
return GetCommonTangents(b, a, pb, pa);
const double PI = std::acos(-1);
Vector link = b.c - a.c;
double d2 = Dot(link, link);
double rDiff = a.r - b.r;
double rSum = a.r + b.r;
double base = std::atan2(link.y, link.x); //极角
if (dcmp(d2) == 0 && dcmp(a.r - b.r) == 0)
return -1; //两圆完全重合(情况 1)
else if (dcmp(d2 - rDiff * rDiff) < 0)
return 0; //内含(情况 2)
else if (dcmp(d2 - rDiff * rDiff < 0))
{
*(pa++) = a.point(base);
*(pb++) = b.point(base);
return 1; //内切(情况 3)
}
INT ret = 0;
//剩下的都有两条外公切线
double ang = std::acos(rDiff / std::sqrt(d2)); //转角
*(pa++) = a.point(base + ang); *(pb++) = b.point(base + ang); ret++;
*(pa++) = a.point(base - ang); *(pb++) = b.point(base - ang); ret++; //外公切线对应向量平行
if (dcmp(d2 - rSum * rSum) == 0) //一条内公切线(情况 5)
{
*(pa++) = a.point(base); *(pb++) = b.point(PI + base); ret++; // b 圆为相反方向(加 PI)
}
else if (dcmp(d2 - rSum * rSum) > 0) //两条外公切线(情况 6)
{
ang = std::acos(rSum / std::sqrt(d2));
*(pa++) = a.point(base + ang); *(pb++) = b.point(PI + base + ang); ret++;
*(pa++) = a.point(base - ang); *(pb++) = b.point(PI + base - ang); ret++; //内公切线相对于极角对称(加 PI)
}
return ret;
}模块 3 几何算法
1. 凸包
Graham 扫描法
Graham 扫描法是一个离线的按极角排序的凸包算法。
首先找到最左且最下的点 (或者最下方最左的点),以 点为极点,对其它点根据极角从小到大排序,然后使用一个栈。依次扫描每个点,当栈中元素不足两个时,直接将点入栈;否则设栈顶下面的那个元素为 ,栈顶为 ,即将要入栈的元素为 。如果有 ,则弹出栈顶;重复这个过程,直到可以入栈为止。最后在栈中的元素即为凸包。排序的时间复杂度为 ,离线处理的时间复杂度为 。
下面给出了一个有效的实现:
Point points[maxn];
bool comp(const Point& a, const Point& b)
{
double x = std::atan2(a.y - points[1].y, a.x - points[1].x);
double y = std::atan2(b.y - points[1].y, b.x - points[1].x);
if (dcmp(x - y)) return x < y;
return Length(a - points[1]) < Length(b - points[1]); // note
}
void Graham()
{
for (int i = 2; i <= n; i++)
if (points[i].x < points[1].x || points[i].x == points[1].x && points[i].y < points[1].y)
std::swap(points[1], points[i]);
std::sort(points + 2, points + 1 + n, comp);
std::vector<Point> s;
s.push_back(points[1]);
for (int i = 2; i <= n; i++)
{
while (s.size() >= 2 && Cross(s[s.size() - 2] - s[s.size() - 1], s[s.size() - 1] - points[i]) < 0)
s.pop_back();
s.push_back(points[i]);
}
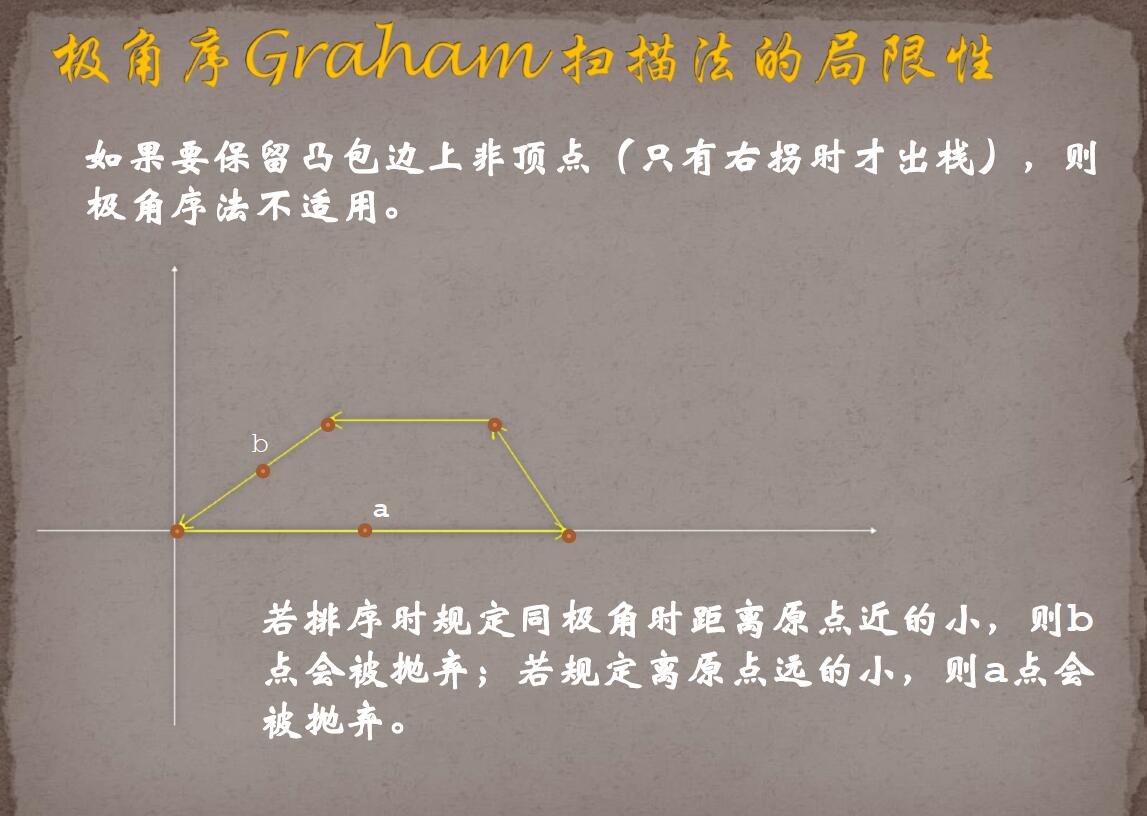
}以上代码能够解决凸包周长的问题。需要注意的是,排序时需要引入距离极点的距离作为第二关键字,否则凸包周长将会求错,原因比较显然。
虽然通过第二关键字的改进能够求得凸包周长,但如果有点在凸包的边上,是无法正确计算出的:
Andrew 扫描法
Andrew 扫描法是 Graham 扫描法的变形。它是一个离线的按坐标排序的凸包算法。它解决了 Graham 算法无法解决的边上的点的问题。
基本思想与 Graham 类似,也是排序后用一个栈判断极角。不同的是排序方法:Andrew 算法直接以 为第一关键字按升序,以 为第二关键字按升序排序。但是 Andrew 一次只能处理半边的凸包,即下半部分的凸包,剩下的需要倒着扫描一次数组再做一次,这种算法保证能够正确得到所有边上的点。
参见代码:倒着扫时需要保证不弹出已经入栈的元素。
Point points[maxn];
bool comp(const Point& a, const Point& b)
{
if (dcmp(a.x - b.x)) return a.x < b.x;
return a.y < b.y;
}
void Andrew()
{
std::sort(points + 1, points + 1 + n, comp);
std::vector<Point> s;
s.push_back(points[1]);
for (int i = 2; i <= n; i++)
{
while (s.size() >= 2 && Cross(s[s.size() - 2] - s[s.size() - 1], s[s.size() - 1] - points[i]) < 0)
s.pop_back();
s.push_back(points[i]);
}
int certain = s.size(); // note
for (int i = n - 1; i >= 1; i--) // note: i >= 1
{
while (s.size() > certain && Cross(s[s.size() - 2] - s[s.size() - 1], s[s.size() - 1] - points[i]) < 0)
s.pop_back();
s.push_back(points[i]);
}
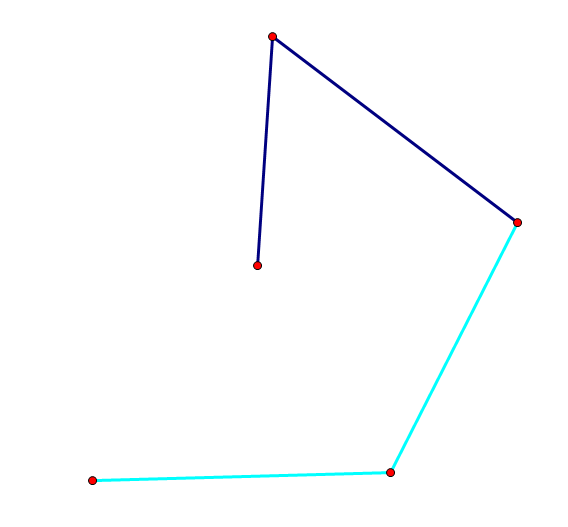
} 需要注意的是,最后那里必须写 i >= 1,处理完后栈顶也一定会是第一个点,否则会出现如图的情况:
相比之下,Graham 算法就不会存在这种问题:按极角排序后保证多边形会是凸的。另外需要注意的是,Andrew 算法只保证逆时针(取决于你的叉积)找到一半凸壳,与第二关键字如何排序无关。