Fractal Streets
这是一道挺有意思的递归问题
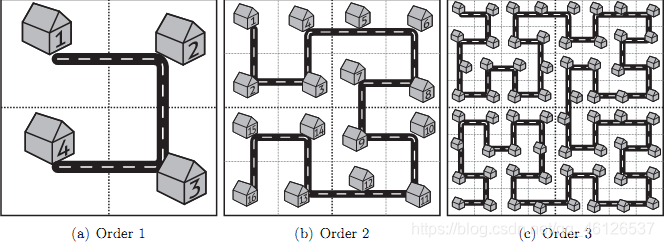
首先我们需要发现不同级分形街道的联系
对于任意一张编号大于2的分形街道来说,右上角右下角的图是由前一张直接平移得到的,左上角的是由前一张顺时针旋转90°得到的,左下角是由前一张逆时针旋转90°得到的
基于这项规律我们可以开始递归
首先我们需要预处理一个边长数组,用来直接获取每一张图的边长
如果一张图中点的编号小于上一张图边长的平方,即可说明这个点是在这张图的左上角的,由此我们可以得到这个点在左下角右上角右下角的判断条件
由每个边的边长通过递归也可以得到这个点的坐标
有了点的坐标当然可以通过两点间距离公式求得距离
在这里距离是需要进行四舍五入的,因此答案要定义成double类型,我在这wa了好几把才发现这个问题
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 40;
ll bc[N]; //存储编号为n的分形图的边长
void find(ll n, ll k, ll &x, ll &y)
{
if (n == 1) //处理边界
{
if (k == 1) x = y = 1;
else if (k == 2) x = 1, y = 2;
else if (k == 3) x = y = 2;
else if (k == 4) x = 2, y = 1;
return;
}
ll sz = (bc[n] / 2) * (bc[n] / 2);
if (k <= sz) //左上
{
dfs(n - 1, k, y, x);
}
else if (k <= 2 * sz) //右上
{
dfs(n - 1, k - sz, x, y);
y += bc[n] / 2;
}
else if (k <= 3 * sz) //右下
{
dfs(n - 1, k - 2 * sz, x, y);
x += bc[n] / 2;
y += bc[n] / 2;
}
else //左下
{
dfs(n - 1, k - 3 * sz, y, x);
x = bc[n] + 1 - x;
y = bc[n] / 2 + 1 - y;
}
}
int main()
{
bc[1] = 2;
for (ll i = 2; i < N; i++)
bc[i] = bc[i - 1] * 2;
ll k;
cin >> k;
while (k--)
{
ll n, h, o;
cin >> n >> h >> o;
ll xh, yh, xo, yo;
find(n, h, xh, yh);
find(n, o, xo, yo);
double res = sqrt((xh - xo) * (xh - xo) + (yh - yo) * (yh - yo)) * 10;
printf("%.0lf\n", res);
}
return 0;
}
Strange Towers of Hanoi
这道题…emm…递推?…DP…
首先给四个柱子编号A BCD,并且预处理得到三柱汉诺塔的答案存再temp数组中
如果先将A上的i个盘子移动到B柱,剩下的ACD柱子就会变成三柱汉诺塔问题
因此对于此时的ACD柱即可运用temp数组求解
对于B柱上的盘子即是res[i]
因此即可得到递推公式2*res[i]+temp[n-i]
#include <bits/stdc++.h>
using namespace std;
const int N = 20;
int main()
{
int temp[N], res[N];
temp[1] = 1;
for (int i = 2; i < 13; i++)
temp[i] = temp[i - 1] * 2 + 1;
memset(res, 0x3f3f3f3f, sizeof(res));
res[1]=1;
for (int i = 1; i < 13; i++)
{
for (int j = 1; j < i; j++) //挪动几个盘子去B柱
res[i] = min(res[i], res[j] * 2 + temp[i - j]);
cout << res[i] << endl;
}
return 0;
}
递归实现指数型枚举
题目太简单了,直接贴代码了
#include <bits/stdc++.h>
using namespace std;
const int N = 10;
int n;
int st[N];
void dfs(int u)
{
if (u == n)
{
for (int i = 0; i < n; i++)
if (st[i] == 1)
cout << i+1 << " ";
cout<<endl;
return ;
}
st[u]=0;
dfs(u+1);
st[u]=-1;
st[u]=1;
dfs(u+1);
st[u]=-1;
}
int main()
{
memset(st, -1, sizeof(st));
cin >> n;
dfs(0);
return 0;
}
递归实现排列类型枚举
题目太简单了,直接贴代码了
#include <bits/stdc++.h>
using namespace std;
const int N=20;
int n;
int res[N];
bool st[N];
void dfs(int u)
{
if(u>n)
{
for(int i=1;i<=n;i++) cout<<res[i]<<" ";
cout<<endl;
return;
}
for(int i=1;i<=n;i++)
{
if(!st[i])
{
res[u]=i;
st[i]=1;
dfs(u+1);
res[u]=0;
st[i]=0;
}
}
}
int main()
{
cin>>n;
dfs(1);
return 0;
}
递归实现组合类型枚举
这个题相比较上两个题只需要多加一个变量存储当前用到了哪一个数即可
#include <bits/stdc++.h>
using namespace std;
const int N=50;
int n,m;
int res[N];
void dfs(int u,int st)
{
if(u+n-st<m) return; //剪枝
if(u==m+1)
{
for(int i=1;i<=m;i++) cout<<res[i]<<" ";
cout<<endl;
return ;
}
for(int i=st;i<=n;i++)
{
res[u]=i;
dfs(u+1,i+1);
res[u]=0; //可以没有
}
}
int main()
{
cin>>n>>m;
dfs(1,1);
return 0;
}
带分数
这道题当然可以直接用dfs暴搜,但是时间复杂度会很高,这里给出一个优化一点的算法
n=a+b/c表示转化一下可以得到b=nc-ac
这样就可以只枚举a和c从而计算出b,实现优化的目的
题目中还有一些隐含条件可以用来剪枝,利用这些条件可以简化
#include <bits/stdc++.h>
using namespace std;
const int N=20;
int n;
int res=0;
bool st[N],mark[N];
bool check(int a,int c)
{
int b=n*c-a*c;
if(!a||!b||!c) return false;
memcpy(mark,st,sizeof(st));
while(b)
{
int x=b%10;
b=b/10;
if(!x||mark[x]) return false;
mark[x]=true;
}
for(int i=1;i<=9;i++)
{
if(!mark[i]) return false;
}
return true;
}
void dfs_c(int u,int a,int c)
{
if(u>9) return;
if(check(a,c)) res++;
for(int i=1;i<=9;i++)
{
if(!st[i])
{
st[i]=true;
dfs_c(u+1,a,c*10+i);
st[i]=false;
}
}
}
void dfs_a(int u,int a) //u表示当前用到了几个数,a表示当前枚举到的a的值
{
if(a>=n) return;
if(a) dfs_c(u,a,0); //带分数中三个数都不能是0,在这里剪枝
for(int i=1;i<=9;i++)
{
if(!st[i])
{
st[i]=true;
dfs_a(u+1,a*10+i);
st[i]=false;
}
}
}
int main()
{
cin>>n;
dfs_a(0,0);
cout<<n<<" ";
cout<<res<<endl;
return 0;
}
翻硬币
这道题是递推的思想
有题目可知,每一枚硬币仅可由前一个硬币和自己来决定是否能进行改变
而且对于任意一个序列都必然有解
因此,首先从第一块硬币开始枚举,如果这个硬币与给出的序列不同,那么就需要对它进行反转,同时对它后面的一个硬币进行反转,重复此操作,就可得到答案
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
char x[N];
char res[N];
void op(int i)
{
if (x[i] == '*') x[i] = 'o';
else x[i] = '*';
}
int main()
{
cin >> x >> res;
int l = strlen(x);
int num = 0;
for (int i = 0; i < l; i++)
{
if (x[i] != res[i])
{
op(i);
op(i + 1);
num++;
}
}
cout << num << endl;
return 0;
}
费解的开关
这道题也是一道利用递推的题目,超级有趣
首先对于任意一个方块,能改变它的只有它自己,以及它四周的方块
因此我们可以这样想,现枚举出第一行的每一种可能性
对于第二行的每一个方块来说,只要它上面的方块是亮的,那么这个方块就必然需要被按下
同样的对于第三行第四行第五行也都是一样
因此如果我们进行这样的操作得不到最后想要的答案就是无解,得到了统计最小步数即可
#include <bits/stdc++.h>
using namespace std;
const int N = 10;
char g[N][N], mark[N][N];
void fun(int x, int y)
{
int dx[5] = {
-1, 0, 1, 0, 0}, dy[5] = {
0, 1, 0, -1, 0};
for (int i = 0; i < 5; i++)
{
int a = x + dx[i], b = y + dy[i];
if (a < 0 || a >= 5 || b < 0 || b >= 5)
continue; // 在边界外
g[a][b] ^= 1; //对灯进行操作
}
}
int main()
{
int k;
cin >> k;
while (k--)
{
for (int i = 0; i < 5; i++)
cin >> g[i];
int res = 10;
for (int op = 0; op < 32; op++)
{
memcpy(mark, g, sizeof(g));
int ans = 0;
for (int i = 0; i < 5; i++) //二进制枚举第一行
{
if (op >> i & 1)
{
ans++;
fun(0, i);
}
}
for (int i = 0; i < 4; i++) //在给定枚举的第一行的条件下解决后面的行数
for (int j = 0; j < 5; j++)
if (g[i][j] == '0')
{
ans++;
fun(i + 1, j);
}
bool f = false;
for (int i = 0; i < 5; i++) //检查是否复合题意
{
if (g[4][i] == '0')
{
f = true;
break;
}
}
if (!f)
res = min(res, ans);
memcpy(g, mark, sizeof(g));
}
if (res > 6)
cout << "-1" << endl;
else
cout << res << endl;
}
return 0;
}
Sumdiv
实在没怎么想明白这道题和递归递推有什么关系
这道题我是直接用数论来求解的
首先对于给定的底数进行因式分解,底数的多少次幂只需要对因式分解后的结果进行相应的幂运算即可
然后利用因数和的公式进行求解
这里用的是等比数列求和公式,注意要将除法转化成乘逆元的形式
因为负数取模的结果依然的负数,所以要对这里的取模进行特殊处理
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MOD = 9901;
unordered_map<ll, ll> vis;
ll qmi(ll a, ll b, ll p)
{
ll res = 1;
while (b)
{
if (b & 1)
res = res * a % p;
a = a * a % p;
b >>= 1;
}
return res;
}
int main()
{
ll a, k;
cin >> a >> k;
if (a == 0)
cout << "0" << endl;
else
{
ll b = a;
for (ll i = 2; i <= b / i; i++)
{
while (b % i == 0)
{
b = b / i;
vis[i]++;
}
}
if (b > 1)
vis[b]++;
ll res = 1;
for (auto i : vis)
{
ll p = i.first, a = i.second * k;
ll t = ((1 - qmi(p, a + 1, MOD)) * qmi(1 - p, MOD - 2, MOD)) % MOD; //除法改成乘逆元的形式
if (t < 0) //对取模进行处理,不得到负数
t = MOD % t;
res = res * t % MOD;
}
cout << res << endl;
}
return 0;
}