握手定理(Handshaking Theorem):握手数之和为偶数,两倍的边数
但是,满足握手定理,握手图不一定存在,比如握手序列(4,4,1,1,1,1)
握手图存在的充要条件:
一个非升序的握手序列:
1.满足握手定理
2. ∀ K ∈ [ 1 , n ] , 前 K 个 度 的 和 ≤ K ( K − 1 ) + ∑ i = K + 1 n m i n ( d i , K ) 2.\forall K \in [1,n],前K个度的和 \leq K(K-1) + \sum_{i=K+1}^{n} min(d_i,K) 2.∀K∈[1,n],前K个度的和≤K(K−1)+∑i=K+1nmin(di,K)
例子:一个三角形
δ ( G ) ≤ 2 , ∃ 环 路 长 度 至 少 为 δ ( G ) + 1 δ(G)\leq 2,\exists 环路长度至少为δ(G)+1 δ(G)≤2,∃环路长度至少为δ(G)+1
证明:
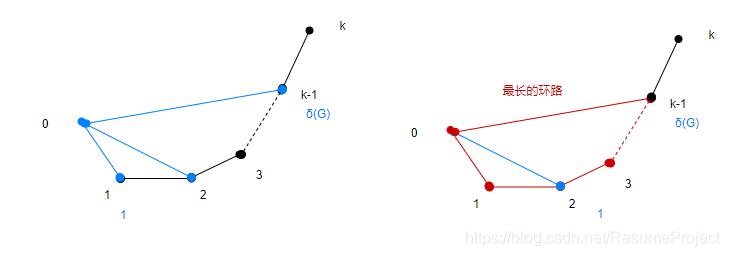
最长路证法
V 0 → V 1 → V 2 → V 3 … … → V k V_0 \rightarrow V_1 \rightarrow V_2\rightarrow V_3……\rightarrow V_k V0→V1→V2→V3……→Vk
则 与 V 0 相 邻 的 顶 点 一 定 在 最 长 路 中 ( 否 则 最 长 路 能 够 增 广 ) 则与V_0相邻的顶点一定在最长路中(否则最长路能够增广) 则与V0相邻的顶点一定在最长路中(否则最长路能够增广)