$AdaptiveTensorLearningwithTensorNetworks(基于张量网络的自适应学习)$

$1.\text{介绍}$

    论文中提出了一种自适应张量学习算法，它与分解模型无关。这个方法依赖于张量网络形式主义，这种形式主义在物理学界取得了巨大的成功，并且最近证明了它在机器学习中压缩模型的潜力，发展了对深层神经网络表达能力的新见解，并设计了监督和非监督学习的新方法。
    这个新的分解模型将在最小化参数数量和最小化给定损失函数之间实现更好的折衷。

    中间展示了一个张量学习框架，介绍这个框架如何自然地从普通的分解模型推广到任意的张量网络。这里定义了一个新的张量优化问题，即在参数数目的约束下，使任意张量网络结构上的损失最小化。由此产生的问题是双层优化问题，其中上层是张量网络结构上的离散优化，下层是给定损失函数的连续优化。论文中提出一个贪婪的方法来优化上层问题，结合自动微分和连续优化技术来优化下层问题。从秩1初始化开始，贪婪算法连续地识别秩增量的张量网络的最有希望的边缘，使得能够从数据中自适应地识别最适合手头任务的张量网络结构。
    在介绍了张量学习框架之后就介绍论文的主题——张量学习的贪婪算法，这个方法是基于一个简单的贪婪方法优化一个可微的损失函数，从一个秩为1的张量开始，连续地为小的秩增量识别最有希望的张量网络边。它能够自适应地识别具有少量参数的张量网络结构，这些参数有效地从数据中优化目标函数。

    最后部分是实验，将不同分解模型与文中的分解模型做了一些对比。

$2.\text{知识回顾}$

    这一部分比较简单。
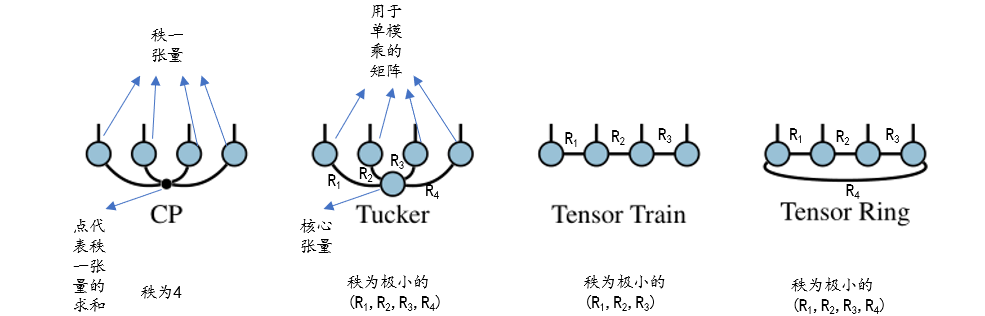
    $CP$分解：把一个张量分解成多个秩一张量的和，张量的秩即为秩一张量的最小个数，这只是严格意义上的，实际不会得到这个严格意义上的张量的秩，而是用低秩去近似。

    $Tucker$分解：把一个张量分解成一个核心张量和多个矩阵的单模乘，每个矩阵的其中一个维度的维数作为秩，这些秩构成的最小元组即为$Tucker$秩，或者多线性秩，这里很好体现了多线性秩。

    $TR$分解：张量环分解，也可以叫$MPS$，因为它实际上是周期性边界条件的$MPS$，$TR$秩即极小的辅助指标元组。

    $TT$分解：开放边界条件的$MPS$，$TT$秩也是极小的辅助指标元组。

$3.\text{张量学习框架}$

考虑如下优化：
$$\underset{\mathcal{W}\in {\mathbb{R}}^{d_1}\times \cdots \times d_p}{\min }\mathcal{L}(\mathcal{W})s.t.\mathrm{rank}(\mathcal{W})\le R$$
    这就是经常见到的所谓低秩近似的最通用的表达形式了，另外s.t. 表示满足……条件。根据前面的知识回顾，这样的表示将发生变化，这就是论文中提到的第一个问题，即损失函数的不同选择导致了不同的常见张量学习问题。
    张量学习框架其实就是给定一个用于张量学习的函数，然后规定损失函数（还会在损失函数后面加个惩罚项），低秩要求作为规范，这是张量学习框架所含的三个部分。
    对于张量秩约束，有两种常见的处理方法，一种是使用凸松弛，然后使用经典的凸优化工具箱来解决由此产生的问题，另一种就是直接使得所给张量的因子最小化从而构造新的损失函数，不过此时这个损失函数是没有前面提到的秩约束的。 后面这种的一个实际例子是$Tucker$分解，其优化只包含了损失函数，而且该函数不再是凸的了，即：
$$\underset{\mathcal{G}\in {\mathbb{R}}^{R_1\times \cdots \times R_p},{\mathbf{U}}_i\in {\mathbb{R}}^{d_i}\times R_i,1\le i\le p}{\min }{\Vert \mathcal{G}{\times }_1{\mathbf{U}}_1{\times }_2\cdots {\times }_p{\mathbf{U}}_p-\mathcal{X}\Vert }_F^2$$
    那么这个与上面的那个有着秩约束的优化有什么区别呢？这个无秩约束的优化实际上是将秩$R$作为一个变量丢进了损失函数，从知识回顾中还可以知道，$Tucker$秩是一个元组,这个元组中秩的选取将影响损失函数的值，这个特点也是本文的关键所在。

$4.\text{张量学习的贪婪算法}$

    对于大多数张量学习问题，没有明确的方法选择使用哪种分解模型。此外，模型不规范的代价可能很高:例如，对于具有低秩的张量，$TT$格式中的最佳低秩近似几乎总是比具有相同参数数的秩分解差。还可能发生的情况是，没有一个常用的模型适合于该任务，并且使用新的张量网络结构将实现最小化参数数量和最小化损失函数之间的最佳折衷。根据任务的不同，实现这种折衷可能有不同的含义:对于张量分解，这将导致更好的压缩比，而对于张量回归，这将导致学习算法的更好的样本复杂性。这些考虑导致我们考虑寻找最佳张量网络结构以最小化给定损失的问题，其中人们希望最小化参数的数量和张量网络实现的目标。当然，具有大量参数的张量网络将倾向于获得较低的损失函数值。陈述问题的一个自然方法是:给定最大参数数的界限，求张量网络结构和最小化给定损失函数的核心张量。
    首先给出规定，${\left(R_{i,j}\right)}_{1\le i<j\le p}$是对张量中单个秩的表示，$i$表示第$i$个节点（感觉用格点描述似乎更好），$j$表示第$j$个节点$R_{i,j}=1$代表没边，大于$1$则代表第$i$个节点和第$j$个节点之间连接了一条维数为 $R_{i,j}$的边，在$MPS$中也可以说多了一个辅助指标。
    把张量$\mathcal{W}\in {\mathbb{R}}^{d_1\times \cdots \times d_p}$ 表示成这样的核心张量的集合 ${\mathcal{G}}^{(1)},\cdots ,{\mathcal{G}}^{(p)}$， 每一个核心张量 ${\mathcal{G}}^{(i)}$ 的尺寸都是 $R_{1,i}\times \cdots \times R_{i-1,i}\times d_i\times R_{i,i+1}\times \cdots \times R_{i,p}.$ 每一个核心张量都是 $p$阶的，但其中有些维度会等于1。 我们用 $\mathrm{T}\mathrm{N}\left({\mathcal{G}}^{(1)},\cdots ,{\mathcal{G}}^{(p)}\right)$ 表示出结果张量。
    例如一个四阶张量可以表示成：
$$\mathrm{TN}{\left({\mathcal{G}}^{(1)},\cdots ,{\mathcal{G}}^{(4)}\right)}_{i_1{i}_2{i}_3{i}_4}=\sum _{j_1^2=1}^{R_{1,2}}\sum _{j_1^3=1}^{R_{1,3}}\cdots \sum _{j_3^4=1}^{R_{3,4}}{\mathcal{G}}_{i_1,j_1^2,j_1^3,j_1^j}{\mathcal{G}}_{j_1^2,i_2,j_2^3,j_2^j}^{\mathcal{G}}{\mathcal{G}}_{j_1^3,j_2^3,i_3,j_3^3}^{(3)}{\mathcal{G}}_{j_1^4,j_2^4,j_3^4,i_4}^{(4)}$$
    这个公式什么意思呢？其实就是对这些辅助指标求和，只保留物理指标，以下图为例：

    一般情况，上面这个$TT$分解只对三个辅助指标求和，但是论文中提出的方法显然不一样，论文中的方法让任意两个格点之间都连接有一个辅助指标，这个操作才是该论文的关键，是最精彩的操作。因为图中的$TT$分解只考虑了相邻格点之间的关系，考虑的是局域，论文中的方法考虑的更全，也考虑了不相邻格点之间的关系，也就是所谓的贪婪的穷举，行就留下，不行的丢弃，很简单的一个道理，对应的优化则是：

$$\underset{\genfrac{}{}{0ex}{}{R_{i,j},}{1\le i<j\le p}}{\min }\underset{{\mathcal{G}}^{(1)},\cdots ,{\mathcal{G}}^{(p)}}{\min }\mathcal{L}\left(\mathrm{TN}\left({\mathcal{G}}^{(1)},\cdots ,{\mathcal{G}}^{(p)}\right)\right)\text{ s.t. }\mathrm{size}\left({\mathcal{G}}^{(1)},\cdots ,{\mathcal{G}}^{(p)}\right)\le C$$
其中$\mathcal{L}$ 是损失函数, 每一个核张量都是$p$阶的，$C$是参数总量。

    另一个问题$2$是双层优化问题，其中上层是张量网络结构上的离散优化，下层是连续优化(假设损失函数是连续的)。 如果有可能求解下层连续优化，则通过枚举上层的搜索空间，即枚举所有满足参数个数约束的张量网络结构，并选择达到目标下限值的一个，可以找到精确解。 这种方法当然是不现实的，因为搜索空间本质上是组合的(其大小将以$W$的数量级呈指数增长)。此外，对于大多数张量学习问题，下层连续优化问题是$NP$难的。论文中提出一种简单的贪婪方法来优化上层问题，结合自动微分和连续优化技术来优化下层问题。

$5.\text{局限性}$

    首先，贪婪算法可能很耗时，因为它必须在每次迭代中测试所有可能的边(张量的二次量级)。然而，这一步是高度可并行化的，并且可以定制高效的特定于任务的试探法来识别要增加的最佳边。
    第二，贪婪算法是解决组合上层离散优化问题的最简单方法之一，并且易于识别次优解。
    最后，贪婪算法学习的张量网络结构不包含超边和内部节点，但贪婪算法可以很容易地解决这个限制，这是留给未来的工作。

$6.\text{算法}$

$$\begin{array}{l}\text{ Algorithm }1\text{ Greedy-TL: Greedy algorithm for tensor learning. }\\ \text{ Input: Loss function }\mathcal{L}:{\mathbb{R}}^{d_1\times \cdots \times d_p}\to \mathbb{R}\text{ , rank increment }R\text{ . }\\ \text{ 1: // Initialize tensor network to a random rank one tensor and optimize loss function. }\\ \text{ 2: }{R}_{i,j}\leftarrow 1\text{ for }1\le i<j\le p\\ \text{ 3: Initialize core tensors }{\mathcal{G}}^{(i)}\in {\mathbb{R}}^{R_{1,i}\times \cdots \times R_{i-1,i}\times d_i\times R_{i,i+1}\times \cdots \times R_{i,p}}\text{ randomly }\\ \text{ 4: }\left({\mathcal{G}}^{(1)},\cdots ,{\mathcal{G}}^{(p)}\right)\leftarrow \text{ optimize }\mathcal{L}\left(\mathrm{TN}\left({\mathcal{G}}^{(1)},\cdots ,{\mathcal{G}}^{(p)}\right)\right)\text{ w.r.t. }{\mathcal{G}}^{(1)},\cdots ,{\mathcal{G}}^{(p)}\\ \text{ 5: repeat }\\ \text{ 6: }(i,j)\leftarrow \text{ find-best-edge }\left(\mathcal{L},\left({\mathcal{G}}^{(1)},\cdots ,{\mathcal{G}}^{(p)}\right)\right)\\ \text{ 7: }{\mathcal{G}}^{(i)}\leftarrow \text{ add-slice }\left({\mathcal{G}}^{(i)},j,R\right)//\text{ add }R\text{ new slices to the jth mode of }{\mathcal{G}}^{(i)}\\ \text{ 8: }{\mathcal{G}}^{(j)}\leftarrow \text{ add-slice }\left({\mathcal{G}}^{(j)},i,R\right)//\text{ add }R\text{ new slices to the ith mode of }{\mathcal{G}}^{(j)}\\ 9:R_{i,j}\leftarrow R_{i,j}+R\\ 10://\text{ Optimize tensor network with rank of edge }(i,j)\text{ increased by }R\\ 11:\left({\mathcal{G}}^{(1)},\cdots ,{\mathcal{G}}^{(p)}\right)\leftarrow \text{ optimize }\mathcal{L}\left(\mathrm{TN}\left({\mathcal{G}}^{(1)},\cdots ,{\mathcal{G}}^{(p)}\right)\right)\text{ w.r.t. }{\mathcal{G}}^{(1)},\cdots ,{\mathcal{G}}^{(p)}\\ 12:\text{ until Stopping criterion }\end{array}$$
其中$w.r.t$意思是关于。
这个算法要表达的其实很简单：
第$2$行和$3$行初始化核心张量（实际上是一个向量），把除了物理指标以外的辅助指标全部置为$1$；
第$4$行初始化原张量的近似，最开始肯定损失很大，随着外循环的进行，损失会变小；
第$5$行就是开始循环，这没写具体情况，但我猜大概是每次循环都设置一个$R$值，这个$R$每次迭代都会加一个固定的值；
第$6$行寻找最好的辅助指标，通过最优化来评估；
第$7$行和第$8$行对最好的辅助指标对应的两个核心张量进行填加片的操作，如果$R$为$1$，这个片是什么依据核心张量的尺寸而定，如果核心张量尺寸为$4\ast 1$，$R=1$，则核心张量尺寸变成$4\ast 2$，这里加的就是一个向量，随着阶数更高，或者$R$（$R$应该是一开始就可以设置的）发生变化；
第$9$行自然是改变对应的辅助指标了；
第$11$行新张量更新；
第$12$行如果未达到收敛条件就继续循环。
算法的思想已经比较明朗了，在$repeat$附近中找每一个$R$下最好的那个辅助指标（边），注意，只找一个，找完后就更新对应核心张量和秩$R$，然后更新新张量，接着判断是否达到收敛条件，没达到就继续下一次迭代找更大秩$R$对应的辅助指标，依次循环知道收敛。

有关片的例子：
    对于一个$4$阶张量, 对 (1,2)边的秩加1需要添加片 $d_1\times R_{1,3}\times R_{1,4}$ (resp. $d_2\times R_{2,3}\times R_{2,4}$ )到 ${\mathcal{G}}^{(1)}(resp.{\mathcal{G}}^{(2)})$上. 经过这个操作后， ${\mathcal{G}}^{(1)}$ 的尺寸为 $d_1\times \left(R_{1,2}+1\right)\times R_{1,3}\times R_{1,4}$ 并且另一个核心张量${\mathcal{G}}^{(2)}$ 的尺寸变为 $\left(R_{1,2}+1\right)\times d_2\times R_{2,3}\times R_{2,4}$，$resp.$意思是替换。

$7.\text{实验}$

$实验一$

    随机生成一个$7\times 7\times 7\times 7\times 7$的张量，然后使用分解模型来分解这个张量，并把不同的分解模型在效果上进行对比。
这是三个初始化的新张量：

    经过自适应学习后其中两个变成：

    效果对比：

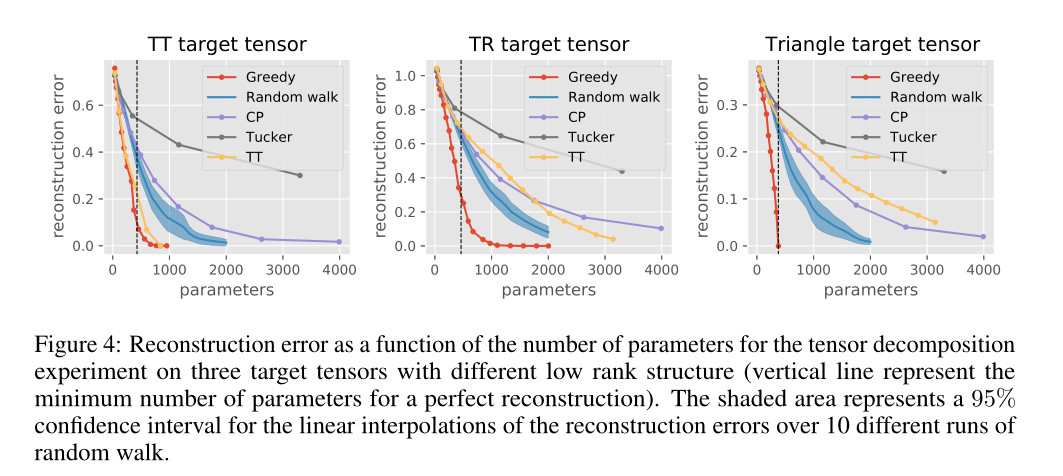
    可以看出，文中提出的$Gready$算法效果好于其他算法。

$实验二$

    将爱因斯坦的人脸图像$resahpe$成$6\times 10\times 10\times 6\times 10\times 10\times 3$的张量后再用不同分解模型对图像进行恢复并对比图像损失，具体如下：

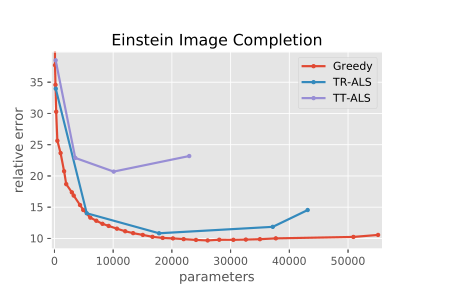
图像恢复效果：

    将Yale 人脸数据库中的图片reshape成$6\times 8\times 6\times 7\times 8\times 19\times 2$的张量后用不同分解模型进行图像恢复并对比图像损失，具体如下：

    从这两张图都可以看出：无论是从参数还是相对误差来看，论文中的算法都优于传统算法的最佳结果。

$8.\text{论文中提到的两个问题}$

    回顾一下论文中所提到的两个问题：
    问题$1$：损失函数的不同选择导致了不同的常见张量学习问题，针对秩约束有两种解决方式，一种是使用凸松弛，然后使用经典的凸优化工具箱来解决，另一种就是直接使得所给张量的因子最小化从而构造新的损失函数，论文中给出的方法就用了这种解决方式，每次迭代处理的都是自以为张量因子的核心张量（格点）。
    问题$2$：双层优化问题，其中上层是张量网络结构上的离散优化（优化的边可能并不连接同一个格点），下层是连续优化(假设损失函数是连续的)，这里应该体现在优化器如何应对损失上面（自动微分或梯度下降），至于论文名为何有个自适应是因为用了一个$RMSprop$优化器，它可以用加权的方式调整学习率，可不就是自适应学习，而且相比动量法（一种优化算法），它进一步优化梯度摆动幅度过大的问题，并进一步加速损失函数的收敛速度。