一.问题背景

基于马尔科夫理论进行预测被认为是一种可行的方法。近年来，结合张量理论和马尔科夫理论进行精准预测，已成为学术界的一种新趋势。
在早期对多阶马尔科夫模型的研究中，是通过多个时刻的线性组合近似为一阶马尔科夫链来处理，但是这种方法难以处理多元多阶马尔科夫模型。
通过张量Z特征分解和多阶马尔科夫理论相结合来进行预测需要 假设任意两个连续时刻的状态发生完全独立，而这种假设现实基本不成立，而且直接利用主Z特征向量进行预测，是不考虑前面m-1个状态的，这和多阶马尔科夫模型是不相匹配的。
现拟解决以下问题：
（1）如何提出一个通用的多元多阶马尔科夫模型，并在没有任何假设的情况下实现状态转移？
（2）如何求解多元多阶马尔科夫模型中的稳态联合概率分布（即：稳态联合主特征张量）？
（3）如何实现基于稳态联合主特征张量的多模态准确预测？

二.多元多阶马尔科夫模型

在一个随机过程中，如果每个状态的影响因素个数为k，我们称该状态为k元状态；如果当前时间的状态是由前m 时刻的状态决定的，我们称该马尔科夫链为m 阶马尔科夫链。因此，多元多阶马尔科夫模型也被称为k元m 阶马尔科夫模型。
为了方便，定义下面两种简化表示的方法：
(1) $k$ 元状态的简化表示: $X_{t, 1}, X_{t, 2}, \cdots, X_{t, k} \Leftrightarrow X_{i} ; i_{t, 1}, i_{t, 2}, \cdots, i_{t, k} \Leftrightarrow i_{t}$
(2) 状态概率的简化表示: $\operatorname{Pr}\left(X_{t}=x_{t}\right) \Leftrightarrow \operatorname{Pr}\left(X_{t}\right) ; \sum_{x_{t}} \operatorname{Pr}\left(X_{t}=x_{t}\right) \Leftrightarrow \sum_{t} \operatorname{Pr}\left(X_{t}\right)$ 。

1.张量连接和张量统一乘

张量连接 : $\quad$ 给定两 $\uparrow$ 张量 $\in R^{I_{1} \times I_{2} \times \ldots \times I_{M} \times K_{1} \times K_{2} \times \ldots \times K_{Q}}$ 和 $\underline{Y} \in R^{K_{1} \times K_{2} \times \ldots \times K_{Q} \times J_{1} \times J_{2} \times \ldots \times J_{N}},$ 他们在 $Q$ 个阶上具有相同维度 $K_{1}, K_{2}, \cdots, K_{Q},$ 则将张量 $\underline{X}$ 和张量 $\underline{Y}$ 进行连接, 将得到一个新的张量 $\underline{Z}\in R^{I_{1} \times I_{2} \times \ldots \times I_{M} \times J_{1} \times J_{2} \times \ldots \times J_{N} \times K_{1} \times K_{2} \times \ldots \times K_{Q}},$ 其运算公式为:
$z_{i_{1}, i_{2}, \cdots, i_{M}, j_{1}, j_{2}, \cdots, j_{N}, k_{1}, k_{2}, \cdots, k_{Q}}=$ oper $\left(x_{i_{1}, i_{2}, \cdots, i_{M}, k_{1}, k_{2}, \cdots, k_{Q}}, y_{k_{1}, k_{2}, \cdots, k_{Q}, j_{1}, j_{2}, \cdots, j_{N}}\right)$

其中 oper 为自定义针对两个实数的运算，该运算可表示为 $\underline{Z}=\underline{X} \bowtie_{Q} \underline{Y}$ 。
示例：
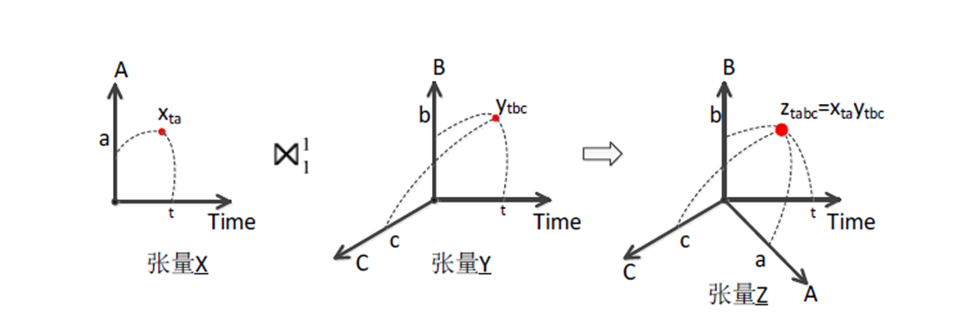
在这里插入图片描述
这里在两个张量元素之间规定的运算是乘法运算，张量沿着time阶连接，这种运算是一种类似模乘但又不是模乘的运算。

张量统一乘：给定两个张量 $\underline{X} \in R^{I_{1} \times I_{2} \times \ldots \times I_{M} \times L_{1} \times L_{2} \times \ldots \times L_{P} \times K_{1} \times K_{2} \times \ldots \times K_{Q}}$ 和 $\underline{Y} \in R^{L_{1} \times L_{2} \times \ldots \times L_{p} \times K_{1} \times K_{2} \times \ldots \times K_{Q} \times J_{1} \times J_{2} \times \ldots \times J_{N}},$ 他们具有两组具有相同维度的阶，包括 $P$ 个用于缩并的阶 $L_{1}, L_{2}, \cdots, L_{P}$ 以及 $Q$ 个用于连接的阶 $K_{1}, K_{2}, \cdots, K_{Q},$ 则将张量 $\underline{X}$ 和张量 $\underline{Y}$ 进行统一乘将得到一个新的张量 $\underline{Z} \in R^{I_{1} \times I_{2} \times \ldots \times I_{M} \times J_{1} \times J_{2} \times \ldots \times J_{N} \times K_{1} \times K_{2} \times \ldots \times K_{Q}},$ 其运算公式为 :
$z_{i_{1}, i_{2}, \cdots, i_{\mu}, j_{1}, j_{2}, \cdots, j_{N}, k_{1}, k_{2}, \cdots, k_{Q}}=\sum_{l_{1}, l_{2}, \cdots, l_{p}} x_{i_{1}, l_{2}, \cdots, i_{M}, l_{1}, l_{2}, \cdots, l_{p}, k_{1}, k_{2}, \cdots, k_{Q}} y_{l_{1}, l_{2}, \cdots, l_{p}, k_{1}, k_{2}, \cdots, k_{Q}, j_{1}, j_{2}, \cdots, j_{N}}$
该运算可表示为 $\underline{Z}=\underline{X} *_{P, Q} \underline{Y}$

示例：
在这里插入图片描述
两个张量在A，B这两个阶作缩并运算，在Time这个阶作连接运算，缩并和连接之间的标记用一个点和一个中文形式的逗号来突出，同作缩并或连接的阶的标记用英文形式的逗号隔开。
在P、Q、M、N取值不同的情况下，张量统一乘可以代表大部分运算。
在这里插入图片描述
前面说过，张量连阶是一种很类似模乘的运算，当只有Q不等于0时，张量统一乘变为张量hadamard积，如果在此基础上Q=2，M=1，这样就是一个三阶张量和一个二阶张量作连接运算，相当于将三阶张量沿着M这一阶一片一片地和二阶张量作hadamard积。

2.多元多阶马尔科夫转移模型

多元多阶马尔科夫转移模型可 借助张量统一乘 得到，首先定义一个状态转移张量 P^’’，对于一个k元m阶的马尔科夫模型，这个状态转移张量的阶数将是k×（m+1）阶，然后定义一个联合概率分布张量 M，它的阶数将是k×m阶。
以一元二阶马尔科夫模型为例：
三阶状态转移张量中的元素为（利用条件概率）：

$\operatorname{Pr}\left(X_{t}=i \mid X_{t-1}=j, X_{t-2}=k, X_{t-3}=i_{t-3}, \cdots, X_{0}=i_{0}\right)=\operatorname{Pr}\left(X_{t}=i \mid X_{t-1}=j, X_{t-2}=k\right)=P_{i j k}^{\prime \prime}$
二阶联合概率分布张量为（利用联合概率）：
$\in R^{I \times I}, m_{i j}=\operatorname{Pr}\left(X_{t}=i, X_{t-1}=j\right)$
通过概率转移理论可得到：
$\left(M^{(t, t-1)}\right)_{(i, j)}=m_{i j}=\operatorname{Pr}\left(X_{t}=i, X_{t-1}=j\right)$
$=\sum_{t-2} \operatorname{Pr}\left(X_{t}=i \mid X_{t-1}=j, X_{t-2}=k\right) \operatorname{Pr}\left(X_{t-1}=j, X_{t-2}=k\right)$
$=\sum_{k} p_{i j k}^{\prime \prime} m_{j k}=\left(\underline{P}^{\prime \prime} *_{t-2}^{t-2, t-1} M^{(t-1, t-2)}\right)_{(i, j)}$
从而一元二阶马尔科夫模型的转移恰好可以由张量统一乘来实现，即：
在这里插入图片描述
下图可加深理解：

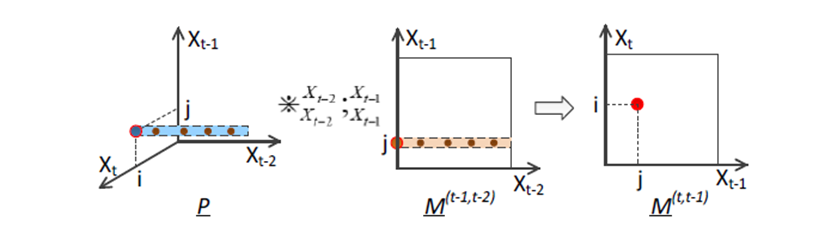
基于张量统一乘的表示方法可以推广到k元m阶马尔科夫模型，即：

用公式可表达为：

从k元m阶马尔科夫模型看，一个状态转移张量包含了m+1个时刻（其中一个时刻是要预测的下一时刻），从一个时刻的整体状态转移到下一时刻的整体状态的概率和为1，一个联合概率分布张量包含了m个时刻，其所有元素概率和为1，并且这两个张量的元素都是大于等于0且小于1的，另外，一个时刻受到 k 种因素影响，这带来的是k阶，每一种因素可以由多种状态，这带来的是维数，每一种因素的状态数不一定是相等的 ，比如一个时刻受到时段和流量两种因素影响，但是时段只能处于1、2两种状态，流量则可处于 A、B、C 三种状态，所以一个时刻所处的状态是一个整体的状态，它是一个序列，每种因素都只能处于一个状态。

3.多元多阶马尔科夫多步转移模型

以下是多步转移模型的两种表达：
在这里插入图片描述

三.多元多阶马尔科夫稳态联合主特征张量

这里提出提出了一种基于张量统一乘的幂法迭代算法来计算多元多阶马尔科夫过程的稳态联合状态概率分布张量，称之为稳态联合主特征张量（Stationary Joint Eigentensor，SJE）。
为保证该基于张量统一乘的迭代幂法算法是收敛的，一种方法是确保多元多阶马尔科夫的转移张量是非周期的和不可约的，如果有周期意味着所处状态具有了周期性，无法保证从任意分布出发，如果可约则意味着限制了一种状态无法到达另外一种状态，这样无法保证平稳分布的唯一性：
$\underline{P^{\prime}}=\alpha \underline{P}+(1-\alpha) \underline{A}$
一个A下面划条横线的张量是修正转移张量，每个值都等于1/(I₁ I₂……I_k)^m+1，等号左边的张量是最后要得到的张量， $\alpha$ 为修正参数，影响收敛速度，剩下的那个张量为初始的转移张量，
另一种等价的方法是对转移过程执行随机性素性修正（公式 (7.11) ）：
在这里插入图片描述
最右边的张量 E 为修正联合概率张量，每个值都等于1/(I₁ I₂……I_k)^m，最左边的张量为稳态联合主特征张量， $\alpha$ 为修正参数，影响收敛速度，P 为要输入的转移张量。
下图为多元多阶马尔科夫稳态联合概率分布张量求解算法：
输入: $k^{*}(m+1)$ 阶转移张量 $\underline{P},$ 以及收敛阈值 $\varepsilon 。$
输出： $k^{*} m$ 阶稳态联合主特征张量 $\underline{M},$ 稳态主特征张量 $\underline{X}$ 。
1: 随机选择一个初始联合状态张量 $\underline{M}^{0},$ 每个元素值为 $/\left(I_{1} I_{2} \cdots I_{k}\right)^{m},$ 且. $\sum \underline{M}^{0}=1$
$\quad$ 令 $j = 0$
3: 执行 $M_{j}=\alpha \underline{P} * \underline{M}_{j-1}+(1-\alpha) \underline{E} ; \quad j=j+1$
$\quad$ 比较 $M_{j}$ 与 $M_{j-1}$ 差的范数 $\quad$ 如果 $\left\|\underline{M}_{j}-\underline{M}_{j-1}\right\|>\varepsilon$ 进入 (3) ;
5: 计算稳态主特征张量 $\underline{X}$ ;
另外我们可以根据实际情况选择合适的范数类型。
关于这个算法的存在性、解的唯一性和收敛性只给出结论：

存在性 : 给定一个 $k$ 元 $m$ 阶马尔科夫过程，假设其 $k^{*}(m+1)$ 阶转移张量为 $\underline{P}$ , 则一定存在一个 $k^{*} m$ 阶的非零非负张量 $\hat{M},$ 即 $\hat{M}=\alpha \underline{P} * \underline{M}+(1-\alpha) \underline{E}, \quad \hat{M}$ 被称为稳态联合状态概率分布张量,也称为稳态联合主特征张量。
唯一性：给定一个 $k$ 元 $m$ 阶马尔科夫过程，假设其 $k$ * $(m + 1)$ 阶转移张量
为 $\underline{P}$ , 则当 $0<\alpha<1$ 时，公式 (7.11) 唯一存在一个解 $\hat{M}$ 。
收敛性: 给定一个 $k$ 元 $m$ 阶马尔科夫过程，假设其 $k^{*}(m+1)$ 阶转移张量为 $\underline{P}$ , M^{(0,-1, \cdots,-m+1)}$ 是为一任意联合状态概率分布张量且满足公式，则当 $0<\alpha<1$ 时，以下定点迭代将收敛于上述唯一性定理中的唯一解:
$\underline{M}^{(t, t-1, \cdots, t-m+1)}=\alpha \underline{P} * \underline{M}^{(t-1, t-2, \cdots, t-m)}+(1-\alpha) \underline{E}$

四.多元多阶马尔科夫多模态预测

多模态预测方法：

基于稳态联合主特征张量的多模态预测方法：给定一个k 元m 阶马尔科夫模型，我们可求得k×m 阶的稳态联合主特征张量。为对未来时刻的状态进行预测，首先需要根据当前场景指定前m-1 个时刻的状态，然后从稳态联合主特征张量种提取第m个时刻的k 阶张量，其代表在前m-1 个时刻的状态都给定情况下下一时刻的稳态状态概率分布。
基于稳态主特征张量的预测方法：通过对过去m-1 个时刻内对所有状态的概率求和，可以计算第m 时刻的稳态状态概率分布张量，即稳态主特征张量（Stationary Eigentensor，SE）。

以上两种方法看上去好像没太大区别，但其实只是在一阶马尔科夫模型上比较相似，两者的差别借助下面的实例可以说明。
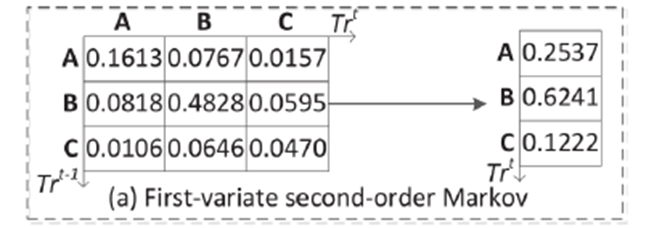
在这里插入图片描述
这是一个联合概率分布矩阵，A、B、C为三种流量状态，Tr^t和Tr^t-1表示两个时刻，按照第一种预测方法，如果规定前一时刻的状态为C，所得稳态状态概率分布张量为【0.0106 0.0646 0.0470】，使用第二种方法则恰得箭头右边的张量，其中每个结果均为分别沿上一时刻概率求和的结果。
下面这个二元二阶马尔科夫模型的联合概率分布张量是类似的：
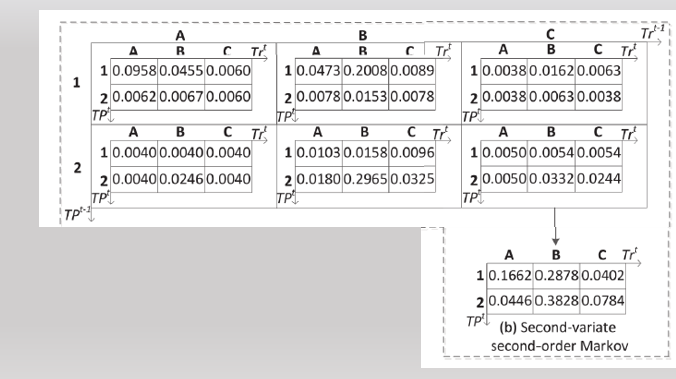
在这里插入图片描述

代码实现

我是先从一元二阶马尔科夫多模态预测的实现开始的，然后才去实现更高元更高阶的马尔科夫多模态预测的代码，代码见下，欢迎与我交流讨论：

import numpy as np
import torch as tc


# 张量统一乘
def uni_tensors(pp, m_matrix, k1, m1, I1, shape):
    p_matrix = tc.reshape(pp, (pow(I1, k1), pow(I1, k1 * m1)))
    m_matrix = tc.reshape(m_matrix, (pow(I1, k1), pow(I1, k1 * (m1 - 1))))
    # 对矩阵化后的联合概率矩阵按列扩展，方便后面的运算
    mn = tc.ones(m_matrix.shape)
    mn.copy_(m_matrix)
    for t in range(0, pow(I1, k1), 1):
        mn = tc.cat((mn, m_matrix), 1)
    # mmm表示张量统一乘后得到的经过向量化的联合概率张量
    mmm = tc.zeros((1, pow(I1, k1 * m1)))
    for x in range(0, pow(I1, k1 * m1), 1):
        mmm[:, x] = p_matrix[:, x] @ mn[:, x]
    return tc.reshape(mmm, shape)


# 求向量的一范数，vector表示向量
def norm1(vector):
    return np.linalg.norm(vector, ord=1)


if __name__ == '__main__':
    # 指定k、m、I，k元m阶马尔科夫模型中的每一个时刻的受到影响因素的个数为I
    k = 2
    m = 2
    I = 3
    # 状态转移张量的形状
    shape1 = []
    for i in range(0, (k * (m + 1)), 1):
        shape1.append(I)
    # 联合概率张量的形状和修正张量的形状
    shape2 = []
    for i in range(0, (k * m), 1):
        shape2.append(I)

    p_zer = tc.ones(shape1)
    p = tc.ones(shape1) / pow(I, k)
    m0 = tc.randint(1, 100, shape2)
    m0_reshape = tc.reshape(m0, (1, pow(I, k * m)))[0]
    m0 = tc.true_divide(m0, norm1(m0_reshape))
    E = tc.ones(shape2) / pow(I, k * m)

    e = 0.0009  # 收敛阈值
    a = 0.9  # 修正参数

    print("状态转移张量为：", p)
    print("初始联合概率张量为：", m0)
    print("设置的收敛阈值为：", e)
    print("设置的修正参数为：", a)
    print("*************************************************************")
    new_m = a * uni_tensors(p, m0, k, m, I, shape2) + (1 - a) * E

    # 计算迭代次数
    count = 0
    while 1:
        print("**************************************************")
        print("联合概率张量更新为:\n", new_m)
        dm = new_m - m0
        dm_reshape = tc.reshape(dm, (1, pow(I, k * m)))
        print("范数：\n", norm1(dm_reshape))
        count += 1
        if norm1(dm_reshape) <= e:
            break
        else:
            m0.copy_(new_m)
            new_m = a * uni_tensors(p, new_m, k, m, I, shape2) + (1 - a) * E
    # 联合主特征张量mm和主特征张量XX

    X1 = tc.reshape(new_m, (pow(I, k * (m - 1)), pow(I, k)))
    # 用来保存经过向量化的稳态主特征张量
    X = tc.zeros((1, pow(I, k)))
    # 主特征张量的形状
    shape3 = []
    for i in range(0, k, 1):
        shape3.append(I)
    # 沿着前m-1个时刻求和得到稳态主特征张量
    for jj in range(0, pow(I, k), 1):
        for z in range(0, pow(I, k * (m - 1)), 1):
            X[:, jj] += X1[z, jj]
    X.copy_(X)
    XX = tc.reshape(X, shape3)
    print("联合主特征张量为：", new_m)
    print("稳态主特征张量为：", XX)
    print("输出范数次数（迭代次数）", count)
    norm = norm1(tc.reshape(new_m, (1, pow(I, k*m)))[0])
    print("联合主特征张量所有元素和为：", norm)

多元多阶的马尔科夫模型的代码实现难度主要在张量统一乘的实现，对于一元二阶马尔科夫模型，其张量统一乘是沿着t-1时刻的所有阶进行1-缩并（即向量与向量求内积映射为一个点），对于多元多阶马尔科夫模型，其张量统一乘是沿着其余时刻的所有阶进行k-缩并，（即k阶张量和k阶张量求“内积”映射为一个点）。
我利用矩阵化的思想将这两个张量的最前面的时刻的所有阶分别作为两个矩阵的行，其余所有阶作为两个矩阵的列，然后还要把矩阵化的联合概率张量列补全得和矩阵化后的状态转移张量的行一样多，然后经过转置后的转移矩阵（矩阵化的状态转移张量）和联合概率矩阵（矩阵化的联合概率张量）将对应行和列进行内积映射为一个点，最后得到一个向量，再将这个向量的形状改为联合概率张量的形状就得到了经过张量统一乘的联合概率张量了，下面这张图可以充分理解这种算法的思想：

在这里插入图片描述

本博客理论部分整理自华中科技大学刘华中的博士学位论文——《基于张量的大数据高效计算及多模态分析方法研究》的第七章基于张量的多元多阶马尔科夫多模态预测方法

基于张量的多元多阶马尔科夫多模态预测方法