最小割小记

关于最小割

常用描述
表述一：删去若干条边使得源点到汇点不连通，求删边的权值和的最小可能值。
表述二：将点集分为 $(S, T)$ ，记所有从 $S$ 中出发到 $T$ 中的边的权值和为 $c (S, T)$ ，求 $c (S, T)$ 的最小值。
求最小割
a. 以权值为容量，该网络最大流的值即为最小割的值
b. 在残量网络中，从源点出发进行一次增广BFS，即得到一个分割。该分割是一个最小割。

题型1：对求最小割原理的理解

[AHOI2009]最小割

[SDOI2014]LIS

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
#define re register
#define maxn 1505
#define LL long long
#define inf 999999999
inline int max(int a,int b){
    
    return a>b?a:b;}
inline int min(int a,int b){
    
    return a<b?a:b;}
inline int read()
{
    
    
    char c=getchar();int x=0;while(c<'0'||c>'9') c=getchar();
    while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-48,c=getchar();return x;
}
struct node{
    
    int a,b,c,rk;}g[maxn];
inline int cmp(node A,node B) {
    
    return A.c<B.c;}
struct E{
    
    int v,nxt,w,f;}e[maxn*maxn];
int n,num=1,S,T,Test;
int ans[maxn],cnt,id[maxn],vis[maxn];
int d[maxn],dp[maxn],head[maxn],cur[maxn],in[maxn],out[maxn];
inline void add(int x,int y,int z) {
    
    e[++num].v=y;e[num].nxt=head[x];head[x]=num;e[num].w=z;}
inline void C(int x,int y,int z) {
    
    add(x,y,z),add(y,x,0);}
inline int check(int s,int t)
{
    
    
    std::queue<int> q;
    memset(vis,0,sizeof(vis));
    q.push(s);vis[s]=1;
    while(!q.empty())
    {
    
    
        int k=q.front();q.pop();
        if(k==t) return 1;
        for(re int i=head[k];i;i=e[i].nxt)
        if(!vis[e[i].v]&&e[i].w>e[i].f) q.push(e[i].v),vis[e[i].v]=1;
    }
    return 0;
}
inline int BFS(int s,int t)
{
    
    
    std::queue<int> q;
    memcpy(cur,head,sizeof(head));
    memset(d,0,sizeof(d));
    d[s]=1,q.push(s);
    while(!q.empty())
    {
    
    
        int k=q.front();q.pop();
        for(re int i=head[k];i;i=e[i].nxt)
        if(!d[e[i].v]&&e[i].w>e[i].f) 
        {
    
    
            d[e[i].v]=d[k]+1;
            if(e[i].v==t) return 1;
            q.push(e[i].v);
        }
    }
    return d[t];
}
int dfs(int x,int now,int t)
{
    
    
    if(x==t||!now) return now;
    int flow=0,ff;
    for(re int& i=cur[x];i;i=e[i].nxt)
    if(d[e[i].v]==d[x]+1)
    {
    
    
        ff=dfs(e[i].v,min(now,e[i].w-e[i].f),t);
        if(ff<=0) continue;
        now-=ff,flow+=ff;
        e[i].f+=ff,e[i^1].f-=ff;
        if(!now) break;
    }
    return flow;
}
int main()
{
    
    
    Test=read();
    while(Test--)
    {
    
    
        n=read();cnt=0;num=1;memset(head,0,sizeof(head));
        for(re int i=1;i<=n;i++) g[i].a=read(),dp[i]=1;
        for(re int i=1;i<=n;i++) g[i].b=read(),g[i].rk=i;
        for(re int i=1;i<=n;i++)
            for(re int j=1;j<i;j++) if(g[j].a<g[i].a) dp[i]=max(dp[j]+1,dp[i]);
        int tot=0;
        for(re int i=1;i<=n;i++) tot=max(tot,dp[i]);
        //dp求LIS 
        T=0;
        for(re int i=1;i<=n;i++) in[i]=++T;
        for(re int i=1;i<=n;i++) out[i]=++T;++T;
        for(re int i=1;i<=n;i++) C(in[i],out[i],g[i].b),id[i]=num;
        for(re int i=1;i<=n;i++) if(dp[i]==1) C(S,in[i],inf);
        for(re int i=1;i<=n;i++) if(dp[i]==tot) C(out[i],T,inf);
        for(re int i=1;i<=n;i++)
            for(re int j=1;j<i;j++) if(g[j].a<g[i].a&&dp[j]+1==dp[i]) C(out[j],in[i],inf);
        tot=0;
        while(BFS(S,T)) 
            tot+=dfs(S,inf,T);
        //建图+跑最小割 
        for(re int i=1;i<=n;i++) g[i].c=read();
        printf("%d ",tot);
        std::sort(g+1,g+n+1,cmp);
        for(re int i=1;i<=n;i++)
        {
    
    
            int k=g[i].rk;
            if(check(in[k],out[k])) continue;
            ans[++cnt]=k;
            while(BFS(T,out[k])) dfs(T,inf,out[k]);
            while(BFS(in[k],S)) dfs(in[k],inf,S);
            e[id[k]].w=e[id[k]^1].w=0;
            e[id[k]].f=e[id[k]^1].f=0;
            //退流，排除和当前所选边等价的边的影响 
        }
        printf("%d\n",cnt);
        std::sort(ans+1,ans+cnt+1);
        for(re int i=1;i<=cnt;i++) printf("%d ",ans[i]);putchar(10);
    }
    return 0;
}

题型2：最下生成树相关

例题这里有

题型3：对点的分割转对边的分割

[HNOI2013] 切糕
在这里插入图片描述

题型4：最小点割集

最小点割集是指：
给出一张有向图（无向图）和两个点S、T，每个点都有一个正数点权，求一个不包含点S、T的权值和最小的点集使得删掉点集中的所有点后，S无法到达T。

求法：
对于这个问题，我们将每一个点拆成两个点，一个为入点，一个为出点，这两个点之间有一条边权为原图中点权的有向边，从入点指向出点。对于原图中的边 $x\to y$ ，我们将其更改为x的出点 $\to y$ 的入点。在转化完的图上跑最小割就是原图的最小点割集。

题型5：最小割树——求任意两点的最小割

最小割树
在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
int n,m,node[505],dep[505],fa[505][10],mn[505][10];
int cnt,top[505],to[1005],len[1005],nex[1005];
int read()
{
    
    
    int re=0;
    char ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch)) re=(re<<3)+(re<<1)+ch-'0',ch=getchar();
    return re;
}
void add_edge(int x,int y,int z)
{
    
    
    to[++cnt]=y,len[cnt]=z,nex[cnt]=top[x],top[x]=cnt;
    to[++cnt]=x,len[cnt]=z,nex[cnt]=top[y],top[y]=cnt;
}
namespace GHT
{
    
    
    int s,t;
    int tot,cur[505],dep[505],col[505],col_bucket[505];
    int cnt=1,top[505],to[3005],cap[3005],flow[3005],nex[3005];
    void add_edge(int x,int y,int z)
    {
    
    
        to[++cnt]=y,cap[cnt]=z,flow[cnt]=0,nex[cnt]=top[x],top[x]=cnt;
        to[++cnt]=x,cap[cnt]=z,flow[cnt]=0,nex[cnt]=top[y],top[y]=cnt;//注意这里 
    }
    bool BFS()
    {
    
    
        memset(cur,0,sizeof cur);
        memset(dep,0,sizeof dep);
        dep[s]=1,cur[s]=top[s];
        queue<int>Q;
        Q.push(s);
        while(!Q.empty())
        {
    
    
            int now=Q.front();Q.pop();
            for(int i=top[now];i;i=nex[i])
                if(!dep[to[i]]&&cap[i]>flow[i])
                {
    
    
                    dep[to[i]]=dep[now]+1;
                    cur[to[i]]=top[to[i]];
                    Q.push(to[i]);
                }
        }
        return dep[t]!=0;
    }
    int DFS(int now,int rest)
    {
    
    
        if(now==t) return rest;
        int re=0;
        for(int &i=cur[now];i;i=nex[i])
            if(dep[to[i]]==dep[now]+1&&cap[i]>flow[i])
            {
    
    
                int lzq=DFS(to[i],min(rest,cap[i]-flow[i]));
                if(lzq)
                {
    
    
                    rest-=lzq,re+=lzq;
                    flow[i]+=lzq,flow[i^1]-=lzq;//注意这里 
                    if(!rest) break;
                }
            }
        return re;
    }
    int Dinic(int x,int y)
    {
    
    
        int re=0;s=x,t=y;
        for(int i=1;i<=cnt;i++) flow[i]=0;
        while(BFS()) re+=DFS(s,0x3f3f3f3f);
        return re;
    }
    void get_color(int now,int color)
    {
    
    
        col[now]=color;
        for(int i=top[now];i;i=nex[i])
            if(cap[i]>flow[i]&&col[to[i]]!=color)//注意这里 
                get_color(to[i],color);
    }
    void build(int l,int r)
    {
    
    
        if(l==r) return ;
        int x=node[l],y=node[l+1];
        int cut=Dinic(x,y);
        get_color(x,++tot);
        int L=l,R=r;
        for(int i=l;i<=r;i++)
            if(col[node[i]]==tot) col_bucket[L++]=node[i];
            else col_bucket[R--]=node[i];
        for(int i=l;i<=r;i++) node[i]=col_bucket[i];
        ::add_edge(x,y,cut);
        build(l,L-1);
        build(R+1,r);
    }
}
void dfs(int now)
{
    
    
    for(int i=1;i<=9;i++)
    {
    
    
        fa[now][i]=fa[fa[now][i-1]][i-1];
        mn[now][i]=min(mn[now][i-1],mn[fa[now][i-1]][i-1]);
    }
    for(int i=top[now];i;i=nex[i])
    {
    
    
        if(to[i]==fa[now][0]) continue;
        dep[to[i]]=dep[now]+1,fa[to[i]][0]=now,mn[to[i]][0]=len[i];
        dfs(to[i]);
    }
}
int getcut(int x,int y)
{
    
    
    int re=INT_MAX;
    if(dep[x]<dep[y]) swap(x,y);
    for(int i=9;i>=0;i--) if(dep[fa[x][i]]>=dep[y]) re=min(re,mn[x][i]),x=fa[x][i];
    if(x==y) return re;
    for(int i=9;i>=0;i--) if(fa[x][i]!=fa[y][i]) re=min(re,min(mn[x][i],mn[y][i])),x=fa[x][i],y=fa[y][i];
    return min(re,min(mn[x][0],mn[y][0]));
}
int main()
{
    
    
    n=read(),m=read();
    while(m--)
    {
    
    
        int x=read(),y=read(),z=read();
        GHT::add_edge(x,y,z);
    }
    for(int i=1;i<=n;i++) node[i]=i;
    GHT::build(1,n);
    dep[1]=1;
    dfs(1);
    m=read();
    while(m--)
    {
    
    
        int x=read(),y=read();
        printf("%d\n",getcut(x,y));
    }
    return 0;
}

题型6：最大权闭合子图

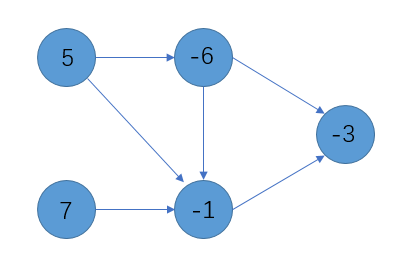
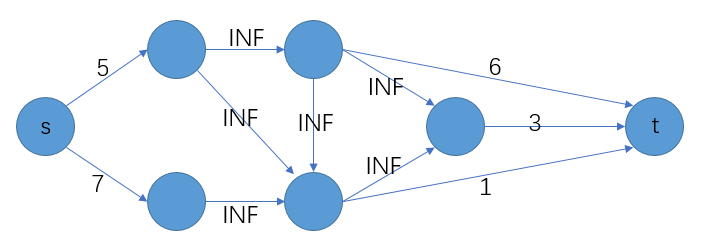
闭合子图指的是，对于有向图，我们选择一些点，在这个点集之中，没有一个点的出边指向非此点集中的点，但是可以有其他点的出边指向这个点集之中。所说的最大权闭合子图，就是在这个图的所有闭合子图中点权和最大的。

求法：
建立源点，向每一个点权为正的点连边，边权为该点的权值。建立汇点，向每一个点权为负连边，边权为该点的权值的绝对值。原图中的边进行保留，边权为 $i n f$ 。最大权闭合子图就是所有的点权为正的点权和减去最小割。

在这里插入图片描述

题型7：划分点集

记 $(u\to v,w)$ 为一条从 $u$ 到 $v$ ，权值为 $w$ 的边。

基础模型

把 $n$ 个点划分到两个集合 $A, B$ 。给出若干形如 “若…，则有…的代价/贡献” 的条件。问最大贡献/最小代价是多少。

如果题目问的是最小代价，直接按下面方法连边求最小割。
如果题目问的是最大贡献，答案为 $\sum 所有可能贡献-最小代价(最小割)$ 。

定义和 $S$ 相连的点划到 $A$ 集合，和 $T$ 相连的点划到 $B$ 集合，那么我们可以按下面的方法处理题目给出的条件：

条件-表述1：若把 $i$ 划到 $A$ ，则要付出 $b_i$ 的代价；若把 $i$ 划到 $B$ ，则要付出 $a_i$ 的代价
条件-表述2：若把 $i$ 划到 $B$ ，则有 $b_i$ 的贡献；若把 $i$ 划到 $A$ ,则有 $a_i$ 的贡献
方案： $(i\to T,b_i)$ , $(S\to i,a_i)$
条件-表述1：若点集 $X$ 中有元素划到 $B$ ，则要付出 $c$ 的代价
条件-表述2：若点集 $X$ 中元素全部划到 $A$ ，则有 $c$ 的贡献
方案： $(S\to new,c),\forall i\in X(new\to i,inf)$
条件-表述1：若点集 $X$ 中有元素划到 $A$ ，则要付出 $d$ 的代价
条件-表述2：若点集 $X$ 中元素全部划到 $B$ ，则有 $d$ 的贡献
方案： $\forall i\in X(i\to new,inf),(new\to T,d)$
条件：若点集 $X$ 中有元素划到 $B$ ，点集 $Y$ 中有元素划到 $A$ ，则要付出 $e$ 的代价
常见形式：若点 $i$ 划到 $B$ ，点 $j$ 划到 $A$ ，则要付出 $e$ 的代价
方案： $\forall i\in X(new1\to i,inf)$ , $\forall j\in Y(j\to new2,inf)$ , $(new2\to new1,e)$
条件：若点集 $X$ 中有元素划到 $A$ ，点集 $Y$ 中有元素划到 $B$ ，则要付出 $f$ 的代价
常见形式：若点 $i$ 划到 $A$ ，点 $j$ 划到 $B$ ，则要付出 $f$ 的代价
方案： $\forall i\in X(i\to new1,inf)$ , $\forall j\in Y(new2\to j,inf)$ , $(new1\to new2,f)$