堆分为两种：最大堆和最小堆，两者的差别在于节点的排序方式。

在最大堆中，父节点的值比每一个子节点的值都要大。在最小堆中，父节点的值比每一个子节点的值都要小。这就是所谓的“堆属性”，并且这个属性对堆中的每一个节点都成立。

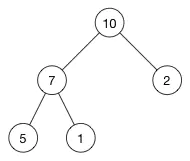
这是一个最大堆，因为每一个父节点的值都比其子节点要大。10 比 7 和 2 都大。7 比 5 和 1都大。

根据这一属性，那么最大堆总是将其中的最大值存放在树的根节点。而对于最小堆，根节点中的元素总是树中的最小值。堆属性非常有用，因为堆常常被当做优先队列使用，因为可以快速地访问到“最重要”的元素。

堆的根节点中存放的是最大或者最小元素，但是其他节点的排序顺序是未知的。例如，在一个最大堆中，最大的那一个元素总是位于 index 0 的位置，但是最小的元素则未必是最后一个元素。–唯一能够保证的是最小的元素是一个叶节点，但是不确定是哪一个。

1堆和普通树的区别

堆并不能取代二叉搜索树，它们之间有相似之处也有一些不同。我们来看一下两者的主要差别：

节点的顺序。在二叉搜索树中，左子节点必须比父节点小，右子节点必须必比父节点大。但是在堆中并非如此。在最大堆中两个子节点都必须比父节点小，而在最小堆中，它们都必须比父节点大。

内存占用。普通树占用的内存空间比它们存储的数据要多。你必须为节点对象以及左/右子节点指针分配内存。堆仅仅使用一个数据来存储数组，且不使用指针。

平衡。二叉搜索树必须是“平衡”的情况下，其大部分操作的复杂度才能达到O(log n)。你可以按任意顺序位置插入/删除数据，或者使用 AVL 树或者红黑树，但是在堆中实际上不需要整棵树都是有序的。我们只需要满足堆属性即可，所以在堆中平衡不是问题。因为堆中数据的组织方式可以保证O(log n) 的性能。

搜索。在二叉树中搜索会很快，但是在堆中搜索会很慢。在堆中搜索不是第一优先级，因为使用堆的目的是将最大（或者最小）的节点放在最前面，从而快速的进行相关插入、删除操作。

2来自数组的树

用数组来实现树相关的数据结构也许看起来有点古怪，但是它在时间和空间上都是很高效的。

我们准备将上面例子中的树这样存储：

[ 10, 7, 2, 5, 1 ]

就这么多！我们除了一个简单的数组以外，不需要任何额外的空间。

如果我们不允许使用指针，那么我们怎么知道哪一个节点是父节点，哪一个节点是它的子节点呢？问得好！节点在数组中的位置index 和它的父节点以及子节点的索引之间有一个映射关系。

如果 i 是节点的索引，那么下面的公式就给出了它的父节点和子节点在数组中的位置：

parent(i) = floor((i - 1)/2)
left(i)   = 2i + 1
right(i)  = 2i + 2

注意 right(i) 就是简单的 left(i) + 1。左右节点总是处于相邻的位置。

注意：根节点(10)没有父节点，因为 -1 不是一个有效的数组索引。同样，节点 (2)，(5)和(1) 没有子节点，因为这些索引已经超过了数组的大小，所以我们在使用这些索引值的时候需要保证是有效的索引值。

在最大堆中，父节点的值总是要大于（或者等于）其子节点的值。这意味下面的公式对数组中任意一个索引 i都成立：

array[parent(i)] >= array[i]

3插入

我们通过一个插入例子来看看插入操作的细节。我们将数字 16 插入到这个堆中：

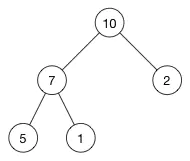
堆的数组是： [ 10, 7, 2, 5, 1 ]。

第一股是将新的元素插入到数组的尾部。数组变成：
[ 10, 7, 2, 5, 1, 16 ]
相应的树变成了：

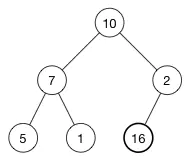
16 被添加最后一行的第一个空位。不行的是，现在堆属性不满足，因为 2 在 16 的上面，我们需要将大的数字在上面（这是一个最大堆）为了恢复堆属性，我们需要交换 16 和 2。

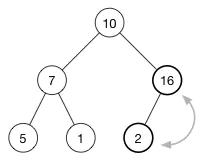
现在还没有完成，因为 10 也比 16 小。我们继续交换我们的插入元素和它的父节点，直到它的父节点比它大或者我们到达树的顶部。这就是所谓的 shift-up，每一次插入操作后都需要进行。它将一个太大或者太小的数字“浮起”到树的顶部。

最后我们得到的堆：

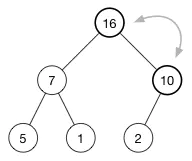
4 删除节点

我们将这个树中的 (10) 删除：

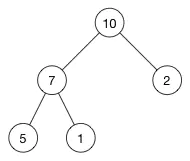
现在顶部有一个空的节点，怎么处理？

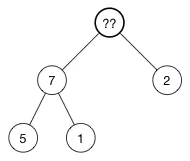
当插入节点的时候，我们将新的值返给数组的尾部。现在我们来做相反的事情：我们取出数组中的最后一个元素，将它放到树的顶部，然后再修复堆属性。

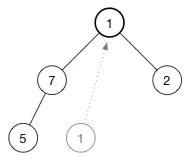
现在来看怎么 shift-down (1)。为了保持最大堆的堆属性，我们需要树的顶部是最大的数据。现在有两个数字可用于交换 7 和 2。我们选择这两者中的较大者称为最大值放在树的顶部，所以交换 7 和 1，现在树变成了：

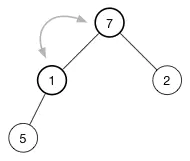
继续堆化直到该节点没有任何子节点或者它比两个子节点都要大为止。对于我们的堆，我们只需要再有一次交换就恢复了堆属性：

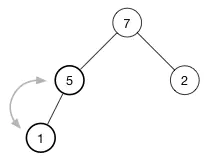
5堆排序的代码

堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。

import java.util.Arrays;

public class Main {
    
    
    public static void main(String[] args) {
    
    
        int[] arr = new int[] {
    
    
                9,8,7,6,5,4,3,2,1
        };
        sort(arr);
        System.out.println(Arrays.toString(arr));
    }

    private static void sort(int[] arr) {
    
    
        // 构建大顶堆
        for (int i = arr.length / 2 - 1; i >= 0; i--) {
    
    
            // 从第一个非叶节点，从上至下，从左至右调整结构
            adjustHeap(arr, i, arr.length);
        }
        // 调整堆结构 +  交换堆顶元素与末尾元素
        for (int j = arr.length - 1; j > 0; j--) {
    
    
            swap(arr, 0, j);
            adjustHeap(arr, 0, j);
        }

    }

    private static void swap(int[] arr, int i, int j) {
    
    
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    // 调整大顶堆（仅是调整过程，建立在大顶堆已构建的基础上）
    private static void adjustHeap(int[] arr, int i, int length) {
    
    
        int temp = arr[i];
        for (int k = 2 * i + 1; k < length; k = k * 2 + 1) {
    
     // 从i结点的左子结点开始，也就是2i+1处开始
            if (k + 1 < length && arr[k] < arr[k + 1]) {
    
    
                k++;
            }
            if (arr[k] > temp) {
    
    
                arr[i] = arr[k];
                i = k;
            } else {
    
    
                break;
            }
        }
        arr[i] = temp;
    }
}