Animation is a math-heavy topic, 这一篇文章主要是实现动画系统需要用到的数学相关的Vector类和矩阵类的代码。
Chapter 2: Implementing Vectors
详细的数学说明可以参考作者写的这篇文章
重点部分:
- Understanding component-wise operations
- Understanding non-component-wise operations
- vector的插值和比较大小
简单Vector介绍
A vector is an n-tuple of numbers.
创建Vector类
这里使用struct来创建,代码如下:
// 放在新创建的vec3.h头文件里
#ifndef _H_VEC3_
#define _H_VEC3_
struct vec3
{
// 这里用了一个匿名的union, 附录会提到unnamed union
// 使用union, 让vec3既能当数组用, 也能当float[3]用
union
{
struct
{
float x;
float y;
float z;
};
float v[3];
};
// 三种构造函数: 默认, xyz和float[3]
inline vec3() : x(0.0f), y(0.0f), z(0.0f) {
}
inline vec3(float _x, float _y, float _z) :
x(_x), y(_y), z(_z) {
}
inline vec3(float* fv) :
x(fv[0]), y(fv[1]), z(fv[2]) {
}
};
#endif
Epsilon
在开始实现vec3的相关函数之前,要考虑一下,浮点数比较的问题,这里要不要使用epsilon值,也就是说当两个浮点数差值绝对值小于epsilon时,认为二者相等,这里认为:
#define VEC3_EPSILON 0.000001f
更多的浮点数比较可以看这里
Finding the right epsilon value to use for comparison operations is dif icult. In this chapter, you declared 0.000001f as the epsilon. This value is the result of some trial and error. To learn more about comparing floating point
values, check out https://bitbashing.io/comparingfloats.html.
component-wise operations
component-wise operation指的是一种运算,翻译过来叫逐组件操作,也就是对vec3的xyz都操作,这里的component-wise operation有:
- 向量的加减
- 向量的Scaling
- 向量的乘法,注意跟点积不一样,点积是得到一个数,而向量乘法是
(x*x, y*y, z*z) - 向量的点积
相关代码如下,挺简单的:
// vec3.cpp里
vec3 operator+(const vec3 &l, const vec3 &r)
{
return vec3(l.x + r.x, l.y + r.y, l.z + r.z);
}
vec3 operator-(const vec3 &l, const vec3 &r)
{
return vec3(l.x - r.x, l.y - r.y, l.z - r.z);
}
// scale
vec3 operator*(const vec3 &v, float f)
{
return vec3(v.x * f, v.y * f, v.z * f);
}
// 向量乘法得到的向量, 方向和大小都完全变了(还不知道会有啥用)
vec3 operator*(const vec3 &l, const vec3 &r)
{
return vec3(l.x * r.x, l.y * r.y, l.z * r.z);
}
// The dot product is used to measure how similar two vectors
float dot(const vec3 &l, const vec3 &r)
{
return l.x * r.x + l.y * r.y + l.z * r.z;
}
non-component-wise operations
比较简单,就这些内容:
// 返回长度的平方
float lenSq(const vec3& v)
{
return v.x * v.x + v.y * v.y + v.z * v.z;
}
float len(const vec3 &v)
{
float lenSq = v.x * v.x + v.y * v.y + v.z * v.z;
if (lenSq < VEC3_EPSILON)
return 0.0f;
return sqrtf(lenSq);
}
// 归一化vector
void normalize(vec3 &v)
{
float lenSq = v.x * v.x + v.y * v.y + v.z * v.z;
if (lenSq < VEC3_EPSILON)
return;
float invLen = 1.0f / sqrtf(lenSq);// 除以模
v.x *= invLen;
v.y *= invLen;
v.z *= invLen;
}
vec3 normalized(const vec3 &v)
{
float lenSq = v.x * v.x + v.y * v.y + v.z * v.z;
if (lenSq < VEC3_EPSILON)
return v;
float invLen = 1.0f / sqrtf(lenSq);
return vec3(v.x * invLen, v.y * invLen, v.z * invLen);
}
// PS: 弧度和degree的转换值为57.2958f和0.0174533f
float angle(const vec3 &l, const vec3 &r)
{
float sqMagL = l.x * l.x + l.y * l.y + l.z * l.z;
float sqMagR = r.x * r.x + r.y * r.y + r.z * r.z;
if (sqMagL<VEC3_EPSILON || sqMagR<VEC3_EPSILON)
return 0.0f;
float dot = l.x * r.x + l.y * r.y + l.z * r.z;
float len = sqrtf(sqMagL) * sqrtf(sqMagR);
return acosf(dot / len);//返回的弧度制
}
// 返回向量A在向量B上的投影向量
vec3 project(const vec3 &a, const vec3 &b)
{
float magBSq = len(b);
if (magBSq < VEC3_EPSILON)
return vec3();
float scale = dot(a, b) / magBSq;
return b * scale;
}
// 其实就是向量a减去a在向量b上的投影
vec3 reject(const vec3 &a, const vec3 &b)
{
vec3 projection = project(a, b);
return a - projection;
}
// 向量Reflection, b是法向量, a是入射向量
// 这个函数经常用于物理和AI, 动画里不一定会用到
vec3 reflect(const vec3 &a, const vec3 &b)
{
float magBSq = len(b);
if (magBSq < VEC3_EPSILON)
return vec3();
// 计算|a|cosθ
float scale = dot(a, b) / magBSq;
vec3 proj2 = b * (scale * 2);
return a - proj2;
}
额外提一下reflect函数的原理,如下图所示,A为入射向量,可以先计算A到B上的投影,得到的投影一个负值,然后再乘以一个-1,那么就是图中的S代表的向量的模,然后乘以向量B,就是S向量,S向量再乘以2,加上原本的A,就得到了反射的A’

向量叉乘
向量的叉乘涉及到一些矩阵的数学,后面会再提到,现在只需要知道,这里的坐标系是左手坐标系,矩阵里是行向量,现在的叉乘需要创建一个3×3的矩阵,矩阵第一行的向量就是叉乘的结果向量,第二行和第三行分别是叉乘算法的输入向量,The value of each component of the result vector is the minor of that element in the matrix
What exactly is the minor of an element in a 3x3 matrix? It’s the determinant of a smaller, 2x2 sub-matrix. A
the minor of an element in a 3x3 matrix?
指的是3×3的矩阵里的2×2的子矩阵对应的行列式(determinant意思是行列式,就是线代里的|M|的值),这里的计算方法就是,Result的每一个Component(xyz),其值就等于除去该行和该列,得到的子行列式的值,如下图所示:

行列式的计算,大学线代学过,交叉乘相减就行了:

所以代码是:
// 叉乘, 好像这里是左手坐标系
vec3 cross(const vec3 &l, const vec3 &r)
{
return vec3(l.y * r.z - l.z * r.y,
l.z * r.x - l.x * r.z,
l.x * r.y - l.y * r.x);
}
顺便再巩固一下,叉乘结果的模与两个向量的θ的sin值有关,公式为:

向量插值
这里提到三种,线性插值Lerp、球形线性插值(spherical linear interpolation)Slerp和NLerp(normalized lerp),区别如下图所示:
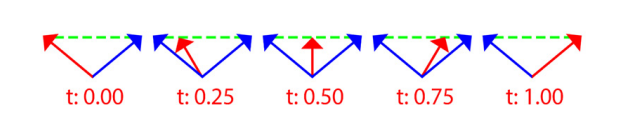
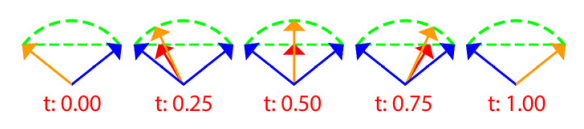
NLerp应该就是把Lerp后得到的向量归一化而已,没啥奇特的:

Slerp的插值方法如下图所示,θ是向量A转到向量B的角度:
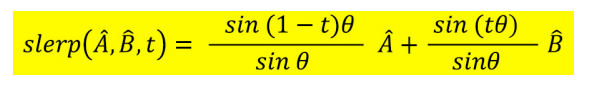
代码如下:
// 线性插值, 算Δ, 乘以t就行了, t一般在[0, 1]内
// 此时的插值是shortest path
vec3 lerp(const vec3 &s, const vec3 &e, float t)
{
return vec3(s.x + (e.x - s.x) * t,
s.y + (e.y - s.y) * t,
s.z + (e.z - s.z) * t);
}
// 球形线性插值, 此时的插值是shortest arc
vec3 slerp(const vec3 &s, const vec3 &e, float t)
{
// 注意, 当t接近0的时候, 要换为lerp(或Nlerp), 原因Remain
if (t < 0.01f)
return lerp(s, e, t);
vec3 from = normalized(s);
vec3 to = normalized(e);
float theta = angle(from, to);// 计算出二者的旋转角度
float sin_theta = sinf(theta);
float a = sinf((1.0f - t) * theta) / sin_theta;
float b = sinf(t * theta) / sin_theta;
return from * a + to * b;
}
// Generally, nlerp is a better choice than slerp. It's a very
// close approximation and much cheaper to calculate.
vec3 nlerp(const vec3 &s, const vec3 &e, float t)
{
vec3 linear(s.x + (e.x - s.x) * t,
s.y + (e.y - s.y) * t,
s.z + (e.z - s.z) * t);
return normalized(linear);
}
Generally, nlerp is a better choice than slerp. It’s a very close approximation and much cheaper to calculate. The only
time it makes sense to use slerp instead is if constant interpolation velocity is required.
向量比较大小
bool operator==(const vec3 &l, const vec3 &r)
{
vec3 diff(l - r);
return lenSq(diff) < VEC3_EPSILON;
}
bool operator!=(const vec3 &l, const vec3 &r)
{
return !(l == r);
}
其他的向量类实现(vec2和vec4)
vec2和vec4类不需要定义任何数学的函数,因为这里仅仅把它们作为容器,用于装在数据传递给GPU,不用于计算。不同于vec3的是,这里的两个向量类都实现两个版本,float版本和int版本,而且这里创建了对应的模板类TVec2和TVec4,后面用个typedef就行了,而且都通过内联函数在header文件里实现,不需要cpp文件,代码如下:
// vec2.h文件里
template<typename T>
struct TVec2
{
union
{
struct
{
T x;
T y;
};
T v[2];
};
inline TVec2() : x(T(0)), y(T(0)) {
}
inline TVec2(T _x, T _y) : x(_x), y(_y) {
}
inline TVec2(T* fv) : x(fv[0]), y(fv[1]) {
}
};
typedef TVec2<float> vec2;
typedef TVec2<int> ivec2;
vec4的内容也类似,不贴出来了,里面的类型比vec2还多一种:
typedef TVec4<float> vec4;
typedef TVec4<int> ivec4;
typedef TVec4<unsigned int> uivec4;
Chapter 3: Implementing Matrices
在游戏动画里,一个矩阵代表一个affine transformation(仿射变换),通过线性变换把点从一个space移到另一个space,这些点通过乘以一个矩阵来变换位置,这章要实现一个4×4的矩阵类,核心内容是:
- Understand column-major matrix storage
- 矩阵乘法和计算矩阵的逆
- 使用矩阵改变vector和points
- 如何可视化一个矩阵:Understand how to create matrices to view a three-dimensional world
本章主要使用代码去介绍矩阵,更全面的参考这里
矩阵基本介绍
矩阵其实就是二维数组,row-major的矩阵,以每行作为vector,column-major的矩阵,以每列作为vector,由于大部分数学书和OpenGL里的矩阵都是用的列向量,所以这里也用这种方式,这种情况下,需要理解矩阵的每个部分代表什么内容,可以熟悉一下这个图:

矩阵的左上角的3×3矩阵里,每一列代表该Transform的旋转变化里的一个basis(基本) vector(each of these is a basis vector for the matrix’s rotation.) The basis vectors are the up, right, and forward directions stored in the matrix. You might have noticed that the rotation and scale components occupy the same space in the matrix. 也就是说,左上角的矩阵,代表了旋转和缩放信息。
需要注意的一点
这里的矩阵是分为列向量的,而C++里的二维矩阵默认是行向量的,这里用C++二维矩阵的行向量来表示矩阵的列向量,也就是说此时的逻辑和实际上的物理内存是有差异的(The basis vectors are the up, right, and forward directions stored in the matrix. You might have noticed that the rotation and scale components occupy the same space in the matrix.)
Creating A Matrix
前面用xyzw和float*来表示vec3,这里同样使用一个union来表示底层数据结构,不过这个union比较庞大:
struct mat4 {
union {
// 方法1. 16个float的数组
float v[16];
// 方法2. 四个列向量对应的vec4, 组成一个struct对象
struct {
vec4 right;
vec4 up;
vec4 forward;
vec4 position;
};
// 方法3. 16个不同命名的float值, 组成一个struct对象(其实就是16个float都加上名字)
struct {
// row 1 row 2 row 3 row 4
/* column 1 */float xx; float xy; float xz; float xw;
/* column 2 */float yx; float yy; float yz; float yw;
/* column 3 */float zx; float zy; float zz; float zw;
/* column 4 */float tx; float ty; float tz; float tw;
};
// 方法4. 使用列在前, 行在后的方式, 取得数组中的元素
struct {
// 注意第一行的c都是c0, 而不是r为r0, 这是因为存的是列
float c0r0; float c0r1; float c0r2; float c0r3;
float c1r0; float c1r1; float c1r2; float c1r3;
float c2r0; float c2r1; float c2r2; float c2r3;
float c3r0; float c3r1; float c3r2; float c3r3;
};
// 方法5. 就是把方法4的变量名掉了个顺序
struct {
float r0c0; float r1c0; float r2c0; float r3c0;
float r0c1; float r1c1; float r2c1; float r3c1;
float r0c2; float r1c2; float r2c2; float r3c2;
float r0c3; float r1c3; float r2c3; float r3c3;
};
};
总之,通过这么一层封装,基本是不再希望直接通过二维矩阵[][]的方式去取元素值了,接下来设计三个类的构造函数,一个默认构造函数,一个构造函数接受一个float*数组作为参数,还有一个构造函数,接受通过输入16个float值的方式作为参数,代码如下:
inline mat4() :
xx(1), xy(0), xz(0), xw(0),
yx(0), yy(1), yz(0), yw(0),
zx(0), zy(0), zz(1), zw(0),
tx(0), ty(0), tz(0), tw(1) {
}
inline mat4(float* fv) :
xx(fv[0]), xy(fv[1]), xz(fv[2]), xw(fv[3]),
yx(fv[4]), yy(fv[5]), yz(fv[6]), yw(fv[7]),
zx(fv[8]), zy(fv[9]), zz(fv[10]), zw(fv[11]),
tx(fv[12]), ty(fv[13]), tz(fv[14]), tw(fv[15]) {
}
// 按照列向量的方式输入
inline mat4(
float _00, float _01, float _02, float _03,
float _10, float _11, float _12, float _13,
float _20, float _21, float _22, float _23,
float _30, float _31, float _32, float _33) :
xx(_00), xy(_01), xz(_02), xw(_03),
yx(_10), yy(_11), yz(_12), yw(_13),
zx(_20), zy(_21), zz(_22), zw(_23),
tx(_30), ty(_31), tz(_32), tw(_33) {
}
}; // end mat4 struct
Common matrix operations
常规的matrix操作跟vec3的差不多,这里先贴出来会有哪些接口:
// mat4.h里声明的接口
// 这些函数作为全局函数, 定义在mat4类外
// 估计是为了降低难度吧, 放在mat4类外就不是运算符重载了
bool operator==(const mat4& a, const mat4& b);
bool operator!=(const mat4& a, const mat4& b);
mat4 operator*(const mat4& m, float f);
mat4 operator+(const mat4& a, const mat4& b);
// To maintain consistency with OpenGL, in this chapter you will be implementing right-to-left multiplication
mat4 operator*(const mat4& a, const mat4& b);
vec4 operator*(const mat4& m, const vec4& v);
vec3 transformVector(const mat4& m, const vec3& v);
vec3 transformPoint(const mat4& m, const vec3& v);
vec3 transformPoint(const mat4& m, const vec3& v, float& w);
void transpose(mat4& m);
mat4 transposed(const mat4& m);
float determinant(const mat4& m);
mat4 adjugate(const mat4& m);
mat4 inverse(const mat4& m);
void invert(mat4& m);
// 包括一些相机矩阵相关的接口, 也放到mat4.h里了
mat4 frustum(float l, float r, float b, float t, float n, float f);
mat4 perspective(float fov, float aspect, float znear, float zfar);
mat4 ortho(float l, float r, float b, float t, float n, float f);
mat4 lookAt(const vec3& position, const vec3& target, const vec3& up);
// 具体的实现在mat4.cpp里
一些简单的矩阵加法的操作就不贴代码了,介绍一些重点操作及相关代码:
矩阵的相等
这里是通过逐元素判断矩阵相等的:
bool operator==(const mat4& a, const mat4& b)
{
for (int i = 0; i < 16; ++i)
{
if (fabsf(a.v[i] - b.v[i]) > MAT4_EPSILON)
return false;
}
return true;
}
bool operator!=(const mat4& a, const mat4& b)
{
return !(a == b);
}
还有一些其他的判定矩阵相等的方法,比如通过比较矩阵的行列式来比较矩阵volume的大小(regardless of shape, the volume of two matrices can be compared using their determinants)。
矩阵用于三维的向量和点
当矩阵用于vector时,它既修改了向量的Scale,也修改了向量的方向,但矩阵作用于点时,它只是对点进行了空间上的平移操作,代数上的二者的区别就是,三维点组成的四维向量的w为1,三维向量组成的四维向量的w为0,注意,这里的矩阵用于二者的函数并没有用*去重载,而是通过函数的方式,避免与矩阵之间的乘法混淆。
代码如下:
// 创建一个简单的宏, 帮助计算, 做了矩阵第mRow行与一个vec4相乘的宏
// 矩阵的名字必须叫m
#define M4V4D(mRow, x, y, z, w) \
x * m.v[0 * 4 + mRow] + \
y * m.v[1 * 4 + mRow] + \
z * m.v[2 * 4 + mRow] + \
w * m.v[3 * 4 + mRow]
// 把vec3当vec4处理, 然后用返回矩阵乘以它的结果, 注意3D向量转为4D向量时, w为0
vec3 transformVector(const mat4& m, const vec3& v)
{
// 其实就是取矩阵的前三行各自与(v, 0.0f)的乘积结果
return vec3(M4V4D(0, v.x, v.y, v.z, 0.0f),// 此值是m的第一行与(v, 0.0f)乘积的结果
M4V4D(1, v.x, v.y, v.z, 0.0f),
M4V4D(2, v.x, v.y, v.z, 0.0f));
}
// 注意, 3D的点转为4D的点时, w为1 (但是不管w为1还是0, 返回的结果好像没有任何影响?)
// (所以和transformVector的区别在哪)
vec3 transformPoint(const mat4& m, const vec3& v)
{
// 其实就是取矩阵的前三行各自与(v, 1.0f)的乘积结果
return vec3(M4V4D(0, v.x, v.y, v.z, 1.0f),
M4V4D(1, v.x, v.y, v.z, 1.0f),
M4V4D(2, v.x, v.y, v.z, 1.0f));
}
矩阵的行列式
it’s important to first understand what the determinant and minor of lower-order matrices are. The determinant function is recursive; to find the determinant of a 4 x 4 matrix, we need to find the determinants of several 3 x 3 and 2 x 2 matrices as well.
只有square 矩阵才有行列式(determinant),矩阵与其转置矩阵的行列式值是相同的
only matrices have a determinant. The determinant of a matrix remains the same if the matrix is transposed.
求矩阵的行列式: 要算出矩阵的行列式,首先要回顾一下之前学的线性代数的东西,余子式,英文里叫矩阵元素的Minor,如下图所示,矩阵第三行第二列的元素M21,其余子式的行列式为右侧的2×2矩阵的行列式:

A matrix of minors is a matrix where every element is the minor of the corresponding element from the input matrix.
由于每个元素都有自己的minor,所以可以形成一个对应的矩阵,每个矩阵的元素都是元素本身对应的minor,这个矩阵里的每个元素,再乘以一个(-1)^(i + j),其中i和j分别代表列号和行号(从0开始),计算得到的结果就叫做COFACTOR(代数余子式),不同矩阵的不同元素位置的符号如下图所示:

之所以提到COFACTOR(代数余子式),是因为它是用于计算矩阵的行列式的,根据拉普拉斯变换(LAPLACE EXPANSION),任何Square矩阵的行列式(determinant),行列式的值等于第一行其各项元素值与各自对应的代数余子式里的值的总和,计算公式如下图所示(我好像记得任意一行或者任意一列都是可以的):

所以这里取第一行元素,算出这个东西就可以了,代码如下:
// 应该是算出4*4矩阵里的三行和三列组成的子矩阵的行列式
#define M4_3X3MINOR(c0, c1, c2, r0, r1, r2) \
(m.v[c0 * 4 + r0] * (m.v[c1 * 4 + r1] * m.v[c2 * 4 + r2] - m.v[c1 * 4 + r2] * m.v[c2 * 4 + r1]) - \
m.v[c1 * 4 + r0] * (m.v[c0 * 4 + r1] * m.v[c2 * 4 + r2] - m.v[c0 * 4 + r2] * m.v[c2 * 4 + r1]) + \
m.v[c2 * 4 + r0] * (m.v[c0 * 4 + r1] * m.v[c1 * 4 + r2] - m.v[c0 * 4 + r2] * m.v[c1 * 4 + r1]))
// 算出4*4矩阵的行列式
float determinant(const mat4& m) {
return m.v[0] * M4_3X3MINOR(1, 2, 3, 1, 2, 3)
- m.v[4] * M4_3X3MINOR(0, 2, 3, 1, 2, 3)
+ m.v[8] * M4_3X3MINOR(0, 1, 3, 1, 2, 3)
- m.v[12] * M4_3X3MINOR(0, 1, 2, 1, 2, 3);
}
伴随矩阵的计算(ADJUGATE)
这里有个伴随矩阵的概念,即A*,A*为A的余子式的矩阵的转置,相关代码如下:
// 返回伴随矩阵A*
mat4 adjugate(const mat4& m) {
// Cofactor(M[i, j]) = Minor(M[i, j]] * pow(-1, i + j)
mat4 cofactor;
// 先计算cofactor(代数余子式)
cofactor.v[0] = M4_3X3MINOR(1, 2, 3, 1, 2, 3);
cofactor.v[1] = -M4_3X3MINOR(1, 2, 3, 0, 2, 3);
cofactor.v[2] = M4_3X3MINOR(1, 2, 3, 0, 1, 3);
cofactor.v[3] = -M4_3X3MINOR(1, 2, 3, 0, 1, 2);
cofactor.v[4] = -M4_3X3MINOR(0, 2, 3, 1, 2, 3);
cofactor.v[5] = M4_3X3MINOR(0, 2, 3, 0, 2, 3);
cofactor.v[6] = -M4_3X3MINOR(0, 2, 3, 0, 1, 3);
cofactor.v[7] = M4_3X3MINOR(0, 2, 3, 0, 1, 2);
cofactor.v[8] = M4_3X3MINOR(0, 1, 3, 1, 2, 3);
cofactor.v[9] = -M4_3X3MINOR(0, 1, 3, 0, 2, 3);
cofactor.v[10] = M4_3X3MINOR(0, 1, 3, 0, 1, 3);
cofactor.v[11] = -M4_3X3MINOR(0, 1, 3, 0, 1, 2);
cofactor.v[12] = -M4_3X3MINOR(0, 1, 2, 1, 2, 3);
cofactor.v[13] = M4_3X3MINOR(0, 1, 2, 0, 2, 3);
cofactor.v[14] = -M4_3X3MINOR(0, 1, 2, 0, 1, 3);
cofactor.v[15] = M4_3X3MINOR(0, 1, 2, 0, 1, 2);
return transposed(cofactor);
}
矩阵的逆
不是所有的矩阵都有逆,只有行列式不为0的矩阵才有逆,在游戏世界里,这个功能经常用于计算View矩阵,也就是把Camera的Transform矩阵,取逆,就能得到View矩阵,在Mesh Skinning里也会用到,后面再提。
矩阵的逆,等于其伴随矩阵除以矩阵的行列式,代码如下:
// 返回逆矩阵
mat4 inverse(const mat4& m)
{
// 先算矩阵的行列式
float det = determinant(m);
// 当矩阵的行列式为0时, 该矩阵没有逆矩阵
if (det == 0.0f)
{
// Epsilon check would need to be REALLY small
std::cout << "WARNING: Trying to invert a matrix with a zero determinant\n";
return mat4();
}
// 计算A*伴随矩阵
mat4 adj = adjugate(m);
// A^-1 = A*/(|A|)
return adj * (1.0f / det);
}
Creating camera matrices
这里为了方便使用,把相机相关的用到矩阵的方式也放到mat4.h和mat4.cpp里了,主要是相机的创建View矩阵的函数,其实游戏里的Camera类,本质就是包含View和Projection两个矩阵信息的对象,这里的投影分为两种,透视投影和正交投影,二者都负责把区域转化到NDC内,也就是-1到1之间到正方体区域,Unlike world/eye coordinates, NDC space is lefthanded.
frustum代表了相机可以看到的区域,书里只给了具体的代码,推导过程要看这里
这里提供了以下几个函数接口:
// 1.1 数学方式直接创建透视投影矩阵
mat4 frustum(float l, float r, float b, float t, float n, float f);
// 1.2 通过更直观的参数来创建透视投影矩阵
mat4 perspective(float fov, float aspect, float n, float f);
// 2. 通过直接的数学运算计算正交投影矩阵, 一般用于2D相机
mat4 ortho(float l, float r, float b, float t, float n, float f);
代码如下:
// 创建frustum代表的透视投影矩阵
mat4 frustum(float l, float r, float b, float t, float n, float f)
{
if (l == r || t == b || n == f)
{
std::cout << "WARNING: Trying to create invalid frustum\n";
return mat4(); // Error
}
return mat4((2.0f * n) / (r - l), 0, 0, 0,
0, (2.0f * n) / (t - b), 0, 0,
(r + l) / (r - l), (t + b) / (t - b), (-(f + n)) / (f - n), -1,
0, 0, (-2 * f * n) / (f - n), 0);
}
// 更直观的创建投影矩阵, 底层还是调用frustum函数
mat4 perspective(float fov, float aspect, float znear, float zfar)
{
// 根据fov和aspect算出frustum的参数
float ymax = znear * tanf(fov * 3.14159265359f / 360.0f);
float xmax = ymax * aspect;
return frustum(-xmax, xmax, -ymax, ymax, znear, zfar);
}
// 正交投影矩阵
mat4 ortho(float l, float r, float b, float t, float n, float f)
{
if (l == r || t == b || n == f)
return mat4(); // Error
return mat4(2.0f / (r - l), 0, 0, 0,
0, 2.0f / (t - b), 0, 0,
0, 0, -2.0f / (f - n), 0,
-((r + l) / (r - l)), -((t + b) / (t - b)), -((f + n) / (f - n)), 1);
}
LookAt函数
参考链接breakdown-of-the-lookAt-function-in-OpenGL
LookAt函数用于创建相机对应的View矩阵,思路上是获取Camera的Transform矩阵,然后取逆,Transform矩阵由TRS三个分量组成,但是Camera没有Scale,所以只计算Translation和Rotation即可。
相机的Transform矩阵会把相机放到世界坐标系的原点,相机看向-Z方向。假设变化之前,Camera位置为position,Camera看到的目标为target,则Camera的朝向为target - position,那么相机可以先旋转到看向-Z的方向,然后平移到原点(注意,这个顺序必须是先旋转,再平移,否则平移之后,再旋转,会绕原点旋转),两个操作对应的矩阵设为R和T,那么有:
// 由于的OpenGL的列向量,坐标左乘M时,会先乘以R
M = TR
此时得到的M矩阵,就是一个仿射变化对应的矩阵,一个仿射变换是一个线性变换加上一个平移变换的组合(An affine transformation is a linear transformation followed by a translation),具体的矩阵的值如下图所示:

也就是说,要求M矩阵的逆矩阵,就是最终的View矩阵,基于线性代数,有:
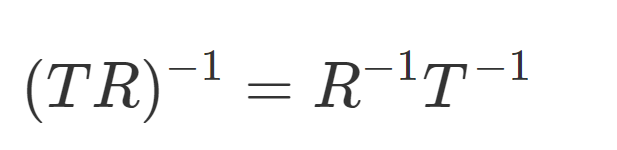
接下来就是求R矩阵和T矩阵的逆了。R矩阵代表从相机的初始Orientation旋转到另外一个Orientation的变换的矩阵,原本的世界坐标系的Rotation是单位矩阵,其basis vector分别为(1,0,0)、(0,0,1)和(0,1,0),而新的camera space的坐标基是可以算出来的,得到的三个坐标基可以直接构造出R矩阵。
计算新的Camera Space下的坐标基
如果说原本的世界坐标系的正交坐标基为(1,0,0),(0,1,0)和(0,0,1),那么新的Camera Space下的正交坐标基,是可以得到的,其中-Z方向是相机的朝向,也就是normalized(target - position),取负就可以得到Z轴上的正交基,然后指定相机的Up向量,可以通过叉乘得到X轴上的正交基,然后X和Z轴上的坐标基再叉乘,可以得到Y轴上的坐标基,这样就计算完成了。
得到了新的坐标基,仍然需要计算R矩阵,Rotation矩阵其实也就是左上角的3×3的部分,这里的坐标基就是R矩阵的这三列的basis vector(具体线性代数上应该有证明,remain)。有了这个结论,就可以直接得到R矩阵,但我们的目标是求R的逆。
此时注意到R矩阵是一个正交矩阵,正交矩阵的逆等于矩阵的转置,所以这下也能避免求矩阵的逆了,有:

而T矩阵的逆,直接带入公式就行了,如下图所示:

所以最后的结果,R的逆乘以T的逆,等于:

可以发现这里的(r11, r12, r13)代表新的x轴的单位向量,这上面计算的结果可以简写成下图,其中e是position的offset向量:

最后写成代码就是这样子:
// position是相机位置, target是相机看的点
mat4 lookAt(const vec3& position, const vec3& target, const vec3& up)
{
// 要把输入位置的相机, 变换到世界坐标系的0,0,0点, 看的方向为Z轴负方向
// 1. 构建出相机的三个basis vector
// f代表看向的目标到相机的方向, 也就是相机看过去的负方向
vec3 f = normalized(target - position) * -1.0f;// 新的相机坐标系的z轴应该是f
vec3 r = cross(up, f); // Right handed 新的相机坐标系的x轴应该是r
if (r == vec3(0, 0, 0))
return mat4(); // Error
normalize(r);
// 为啥还要cross一次, 输入的up直接normalize不就行了么?
// 这是因为, 不可以保证相机看到方向和Up方向正好是正交的, 而且cross(up, f)并不需要
// 相机看的方向和Up方向是正交的, 只要取得垂直与这个面的向量作为r就行了
vec3 u = normalized(cross(f, r)); // Right handed
// 2. 直接算Translation数据
vec3 t = vec3(-dot(r, position),
-dot(u, position),
-dot(f, position));
// 3. 根据公式带入, 矩阵是按列输入的
return mat4(// Transpose upper 3x3 matrix to invert it
r.x, u.x, f.x, 0,
r.y, u.y, f.y, 0,
r.z, u.z, f.z, 0,
t.x, t.y, t.z, 1);
}
Note
由于这里的矩阵的cpp代码里使用了很多宏,为了方便Debug,作者在Github上还提供了额外的没有宏的版本的代码,作者叫它lower-order matrices
Matrices that only encode the position and rotation can be inverted faster because the inverse of a 3 x 3 rotation matrix is the same as its transpose. You will learn how to implement this fast inverse in the next section when implementing the lookAt function.
附录
匿名union和匿名struct
这里写的很清楚,示例代码如下:
// C Program to demonstrate working of anonymous union
#include <stdio.h>
struct Scope {
// Anonymous union
union {
char alpha;
int num;
};
};
int main()
{
struct Scope x;
x.num = 65;
x.alpha = 'A';
// Note that members of union are accessed directly
printf("x.alpha = %c, x.num = %d", x.alpha, x.num);
return 0;
}
旋转矩阵的Basis Vector
一个单位矩阵对应的旋转,它的正交基为(1,0,0)、(0,1,0)和(0,0,1),然后有个新的旋转,其正交基为ABC,为啥对应的旋转矩阵的Basis Vector就是这个正交基ABC
感觉这个问题可以转换为,已知一个旋转的Foward、Up和Right三个向量的任意两个(第三个可以由其他两个叉乘得到),求该旋转对应的Rotation矩阵,或者Quatenion,为啥就能直接写出来?
这个问题Remain,需要补充线性代数知识,还有Basis Vector与Local Axis的关系
顺便提一下,Unity里,一个物体对应的LocalRotation,乘以(1,0,0),得到的向量就是它的LocalTransform的红色箭头,应该也跟这个有关。