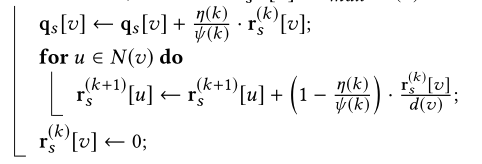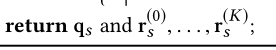西八，看完上篇老师又让看这篇，麻了

2 PRELIMINARIES

2.1 Basic Terminology

依旧是老生常谈的那几个定义：
$G=(V,E)$无向无权图，$d(v)$是v的度，$A$是G的邻接矩阵，$D$是G的对角度矩阵，随机游走矩阵$P=D^{-1}A$。$P^k[s,v]$表示从s出发的一个k跳的随机游走将到达v的概率。

我们希望的是最小化导率：

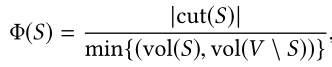
2.2 Heat Kernel-based Local Clustering

给定一个常数t，两个节点u,v，heat-kernel定义从u出发的k跳路径将终结于v的概率为：
$$\eta (k)=\frac{e^{-t}{t}^k}{k!}\text{\hspace{1em}(1)}$$

令s为本地聚类的种子节点，我们定义HKPR向量${\rho }_s$为一个size为n的向量，其中
$${\rho }_s[v]=\sum _{k=0}^{\infty }\eta (k)\ast P^k[s,v]\text{\hspace{1em}(2)}$$

3 SOLUTION OVERVIEW

我们要求我们求得的${\rho }_s^1$应该是$(d,{ϵ}_r,\delta )-approximateHKPR$。这个东西的定义为：
令${\rho }_s$为种子节点s对应的HKPR向量，${\rho }_s^1$为我们求得的的HKPR向量，${\rho }_s^1$是一个$(d,{ϵ}_r,\delta )-approximateHKPR$如果它满足下面这个式子：

换句话说，当$\frac{{\rho }_s[v]}{d[v]}$大于$\delta$时我们要求$\frac{{\rho }_s^1[v]}{d[v]}$提供一个相对误差。当$\frac{{\rho }_s[v]}{d[v]}$小于$\delta$时我们要求$\frac{{\rho }_s^1[v]}{d[v]}$提供一个绝对误差。
这是为了确保当我们使用$\frac{{\rho }_s^1[v]}{d[v]}$排序节点时，这个序列很接近于$\frac{{\rho }_s[v]}{d[v]}$产生的序列。

通过式子(2)定义的HKPR，节点v的HKPR值是所有的从s到达v的k跳的加权和。因此，一个很直接的计算$(d,{ϵ}_r,\delta )-approximateHKPR$的方法是计算大量的随机游走。每一次随机游走从s出发，每一次游走的长度服从式子(1)的泊松分布（这里我理解就是每一次游走的k服从这个分布，更有可能进行步数较短的随机游走）。令$n_r$是总共的随机游走的次数，${\rho }_s^1[v]$是随机游走走到v的分数，我们使用${\rho }_s^1[v]$当作${\rho }_s[v]$估计。
可以证明${\rho }_s^1[v]$是$(d,{ϵ}_r,\delta )-approximateHKPR$的概率至少是：

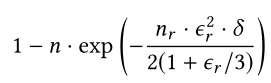
因此，如果我们想要确保这个概率至少是$1-p_f$，我们只需要设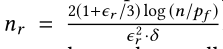因此，这个随机游走需要的时间是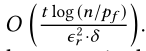
这种方法的问题是开销相当大，为了解释这一点，我们考虑一个点v，这个点有一个很小的${\rho }_s[v]$，但是${\rho }_s[v]/d[v]$却大于$\delta$，根据要求，我们需要保证${\rho }_s^1[v]-{\rho }_s[v]<={ϵ}_r\ast {\rho }_s[v]$。因此，这要求随机游走的次数KaTeX parse error: Undefined control sequence: \n at position 1: \̲n̲_r的次数应该很大，否则，到达v的游走的次数将会很小，${\rho }_s[v]$的估计将会不精准。

为了克服这些困难，我们在第4节和第5节提出了两种更高效的HKPR算法，满足以下两个条件：

1. 以至少$1-p_f$的概率返回一个$(d,{ϵ}_r,\delta )-approximateHKPR$，其中$p_f$是一个用户定义的参数。
2. 运行时间是。

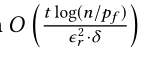4 THE TEA ALGORITHM

这一节我们提出了tea算法，tea算法是为了解决上文中说的算法的低效而提出的，tea算法的思想就是：先使用一个快速的算法计算出HKPR的估计值，然后再利用上文中的方法进行精确计算。

4.1 HK-push

算法1展示了粗略估计的伪代码。
基本想法就是开始设一个向量${\rho }_s$ 只有${\rho }_s[s]=1$，其他值都为0。从s开始对G进行遍历，再遍历的过程中更新${\rho }_s$。值得注意的是，这个过程不仅返回粗略估计的$q_s$，而且返回$r_s^{(k)}$。
在上面这个算法中，
$$\psi (k)=\sum _{l=k}^{\infty }\eta (l)$$

可以发现，在HK-push结束之后，所有的$r_s^{(k)}$向量中还保存着一些值，也就是说那些满足$$r_s^{(k)}<=r_{max}\ast d(v)$$的值被保存了下来。这就像是吃鸡柳棒，吃完之后鸡柳棒上面还残存着没吃干净的鸡丝，我们只需要再把鸡丝给撸下来就算是吃完了一根鸡柳棒。

扫描二维码关注公众号，回复： 13431359 查看本文章

引理1

考虑算法1中的迭代，我们令$q_s$和$r_s^{(0)},r_s^{(1)},\dots r_s^{(K)}$是粗略估计的向量和剩余向量。我们有：
$${\rho }_s[v]=q_s[v]+\sum _{u\in V}\sum _{k=0}^K{r}_s^{(k)}[u]\ast h_u^{(k)}[v]$$
其中$h_u^{(k)}[v]$表示第k跳在u点，这个随机游走最终会落在v点的概率。

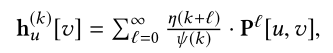
4.2 Algorithm

基本想法：我们上面提到真实的HKPR向量可以被KaTeX parse error: Expected '}', got 'EOF' at end of input: …)，和h_u^{(k)}[v]表示。
回忆一下，$q_s,r_s^{(k)}$我们已经有了，如果我们可以精确地计算出$h_u^{(k)}[v]$对于任意给定的u,v,k，那么我们就可以使用上面的公式精确地计算${\rho }_s$。

引理2：给定G,u,k,对于任意一点v，算法2以概率$h_u^{(k)}[v]$返回v。

算法详细内容：
算法3详细说明了TEA的伪代码

1. 使用HK-push，返回一个粗略的$\rho$值和K+1个残存向量。
2. 使用k-RandomWalk重新计算$\rho$：

• 首先计算残存总和$\alpha$：也就是说$r_s^{(0)},\dots \dots r_s^{(K)}$中不为0的数的总和。
• 计算
  
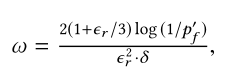
• 其中
  
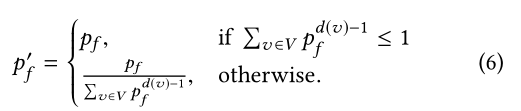
  可以看出$p_f^{{}^{\prime }}$在图G被传入的时候就可以计算出来。
• 给定$\omega$，我们进行k-RandomWalk随机游走的次数定义为$n_r=\alpha \ast \omega$。每一次随机游走k-RandomWalk的参数是随机采样的，采样的概率为$\frac{r_s^{(k)}[u]}{\omega }$。在采样时，我们只需要注意剩余向量中不为0的那些元素就好了。每一次随机游走终结于节点v时，TEA算法增加${\rho }_s^1[v]$，增加了$\alpha /n_r$。

我们观察到TEA算法中的$r_{max}$控制着两个组件的平衡:HK-Push和k-RandomWalk。如果$r_{max}$很小，那么随机游走会变少，但是HK-Push的开销会变大。（其实就是牙缝变小了，鸡柳棒上面剩的的肉丝变少了，但是第一步得啃得比较干净）。相反，HK-Push的开销会变小，但是第二步随机游走的开销会变大。

为了达到这两个算法的平衡，我们设置$r_{max}=O(\frac{1}{\omega \ast t})$。这样的话HK-Push的时间复杂度是$O(\omega \ast t)$，k-RandomWalk的时间复杂度是$O(\alpha \omega t)$

Tea+:

hk-push+: