1. 弗洛伊德(Floyd)算法介绍

上一篇我们讲解了迪杰斯特拉算法的介绍和最短路径问题程序实现，迪杰斯特拉算法是求一个开始顶点到其它多个顶点的最短路径

而弗洛伊德(Floyd)算法中，每一个顶点都是开始顶点，再求一个开始顶点到其它多个顶点的最短路径

2. 弗洛伊德(Floyd)算法的原理

步骤：

1. 将7个顶点分别作为中间顶点、访问顶点、目标顶点，形成一个三层的for循环进行处理
2. 如果访问顶点到中间顶点 + 中间顶点到目标顶点的权重值和，比访问顶点到目标顶点的权重值小，则更新访问顶点到目标顶点的权重值

原理：

• 当以顶点A为中间顶点，其实就是将CAG、CAB、GAB所在的两条边构成的三角形的另一条边连接起来，表示找到最小权重值
• 其它顶点作为中间顶点的情况，和以顶点A作为中间顶点的情况一样。不懂的，自己可以画图试下
• 在三层for循环中，动态的找到所有两点之间的最小权重值

3. 最短路径问题介绍

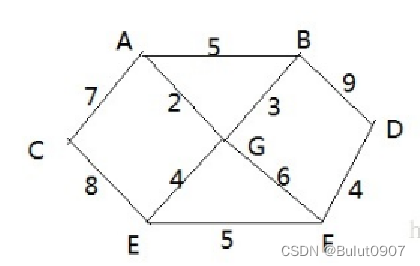
问题：有7个村庄A、B、C、D、E、F、G，各个村庄之间的距离(权)用边线表示，比如A -> B距离5公里。现需要求各个村庄之间的最短路径。即A -> E、B -> F、C -> D等

程序如下：

import java.util.Arrays;

public class FloydAlgorithm {

    public static void main(String[] args) {
        char[] vertexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};

        // 用10000表示距离无限大，不能连通
        final int INFINITY = 10000;
        // N个顶点形成的N * N二维数组，用来保存顶点之间的距离
        // 用INFINITY表示距离无限大，不能连通
        int[][] weights = {
                {0, 5, 7, INFINITY, INFINITY, INFINITY, 2},
                {5, 0, INFINITY, 9, INFINITY, INFINITY, 3},
                {7, INFINITY, 0, INFINITY, 8, INFINITY, INFINITY},
                {INFINITY, 9, INFINITY, 0, INFINITY, 4, INFINITY},
                {INFINITY, INFINITY, 8, INFINITY, 0, 5, 4},
                {INFINITY, INFINITY, INFINITY, 4, 5, 0, 6},
                {2, 3, INFINITY, INFINITY, 4, 6, 0}
        };

        // 创建Graph对象
        Graph graph = new Graph(vertexs, weights);

        // 弗洛伊德算法测试
        graph.floyd();
        graph.show();
    }

}

// 图
class Graph {
    // 顶点集合
    private char[] vertexs;
    // N个顶点形成的N * N二维数组，用来保存顶点之间的距离
    // 在算法执行过程中，会动态的更新weights。最后的结果也保存在weights中
    private int[][] weights;
    // 保存每个顶点在路径上的前一个顶点的index
    private int[][] preVertexIndexs;

    // 构造器
    public Graph(char[] vertexs, int[][] weights) {
        this.vertexs = new char[vertexs.length];
        for (int i = 0; i < vertexs.length; i++) {
            this.vertexs[i] = vertexs[i];
        }

        this.weights = new int[vertexs.length][vertexs.length];
        for (int i = 0; i < vertexs.length; i++) {
            for (int j = 0; j < vertexs.length; j++) {
                this.weights[i][j] = weights[i][j];
            }
        }

        this.preVertexIndexs = new int[vertexs.length][vertexs.length];
        // 每个顶点在路径上的前一个顶点即中间顶点，所以初始化为开始顶点的index
        for (int i = 0; i < vertexs.length; i++) {
            Arrays.fill(this.preVertexIndexs[i], i);
        }
    }

    // 弗洛伊德算法实现
    public void floyd() {
        // 保存访问顶点到中间顶点 + 中间顶点到目标顶点的权重值和
        int tmpWeight = 0;

        // 当以顶点A为中间顶点，其实就是将CAG、CAB、GAB所在的两条边构成的三角形的另一条边连接起来，表示找到最小权重值
        // 其它顶点作为中间顶点的情况，和以顶点A作为中间顶点的情况一样。不懂的，自己可以画图试下
        // 在三层for循环中，动态的找到所有两点之间的最小权重值

        // 对中间顶点遍历，{A, B, C, D, E, F, G}
        for (int midVertexIndex = 0; midVertexIndex < vertexs.length; midVertexIndex++) {
            // 对访问顶点遍历，{A, B, C, D, E, F, G}
            for (int visitVertexIndex = 0; visitVertexIndex < vertexs.length; visitVertexIndex++) {
                // 对目标顶点进行遍历，{A, B, C, D, E, F, G}
                for (int targetVertexIndex = 0; targetVertexIndex < vertexs.length; targetVertexIndex++) {
                    // 求出访问顶点到中间顶点 + 中间顶点到目标顶点的权重值和
                    tmpWeight = weights[visitVertexIndex][midVertexIndex] + weights[midVertexIndex][targetVertexIndex];
                    // 如果计算的权重值和tmpWeight，小于之前的访问顶点到目标顶点的权重值，则进行权重值更新
                    if (tmpWeight < weights[visitVertexIndex][targetVertexIndex]) {
                        weights[visitVertexIndex][targetVertexIndex] = tmpWeight;

                        // 更新一个顶点在路径上的前一个顶点的index
                        // 访问顶点到目标顶点的前一个顶点index，等于中间顶点到目标顶点的前一个顶点的index
                        //      1. 如果中间顶点和目标顶点是直连的，则这个index就是中间顶点的index
                        //      2. 如果中间顶点和目标顶点不是直连的，就会以相同的方式递归到目标顶点的前一个顶点的index
                        preVertexIndexs[visitVertexIndex][targetVertexIndex] = preVertexIndexs[midVertexIndex][targetVertexIndex];

                    }
                }
            }
        }
    }

    // 显示weights和preVertexIndexs
    public void show() {
        char[] vertexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};

        // weights输出一行，preVertexIndexs再输出一行
        for (int i = 0; i < vertexs.length; i++) {
            // 输出weights的一行数据
            for (int j = 0; j < weights.length; j++) {
                System.out.print("(" + vertexs[i] + "到" + vertexs[j] + "的最短路径是" + weights[i][j] + ") ");
            }
            System.out.println();

            // 输出preVertexIndexs的一行的多个index，对应的顶点
            for (int j = 0; j < preVertexIndexs.length; j++) {
                System.out.print(vertexs[preVertexIndexs[i][j]] + " ");
            }
            System.out.println();
            System.out.println();
        }

    }

}

运行程序，结果如下：

(A到A的最短路径是0) (A到B的最短路径是5) (A到C的最短路径是7) (A到D的最短路径是12) (A到E的最短路径是6) (A到F的最短路径是8) (A到G的最短路径是2) 
A A A F G G A 

(B到A的最短路径是5) (B到B的最短路径是0) (B到C的最短路径是12) (B到D的最短路径是9) (B到E的最短路径是7) (B到F的最短路径是9) (B到G的最短路径是3) 
B B A B G G B 

(C到A的最短路径是7) (C到B的最短路径是12) (C到C的最短路径是0) (C到D的最短路径是17) (C到E的最短路径是8) (C到F的最短路径是13) (C到G的最短路径是9) 
C A C F C E A 

(D到A的最短路径是12) (D到B的最短路径是9) (D到C的最短路径是17) (D到D的最短路径是0) (D到E的最短路径是9) (D到F的最短路径是4) (D到G的最短路径是10) 
G D E D F D F 

(E到A的最短路径是6) (E到B的最短路径是7) (E到C的最短路径是8) (E到D的最短路径是9) (E到E的最短路径是0) (E到F的最短路径是5) (E到G的最短路径是4) 
G G E F E E E 

(F到A的最短路径是8) (F到B的最短路径是9) (F到C的最短路径是13) (F到D的最短路径是4) (F到E的最短路径是5) (F到F的最短路径是0) (F到G的最短路径是6) 
G G E F F F F 

(G到A的最短路径是2) (G到B的最短路径是3) (G到C的最短路径是9) (G到D的最短路径是10) (G到E的最短路径是4) (G到F的最短路径是6) (G到G的最短路径是0) 
G G A F G G G