使用递归进行回溯

回溯是一种递归地解决问题的算法技术，它试图逐步建立一个解决方案，一次一个，删除那些在任何时间点上不能满足问题约束的解决方案（这里的时间是指到达搜索树的任何一层所花费的时间）。逆向追踪也可以说是对蛮力方法的改进。

因此，基本上，回溯技术背后的想法是，它在所有可用的选项中搜索一个问题的解决方案。最初，我们从一个可能的选项开始回溯，如果该问题通过所选的选项得到解决，那么我们就返回解决方案，否则就回溯并从剩余的可用选项中选择另一个选项。也有可能出现这样的情况：

没有一个选项会给你带来解决方案，因此我们可以理解为回溯不会给这个特定问题带来任何解决方案。我们也可以说，回溯是一种递归的形式。这是因为从各种可用的选项中寻找解决方案的过程是递归的，直到我们找不到解决方案或达到最终状态。

因此，我们可以得出结论，每一步的回溯都会消除那些不能给我们带来解决方案的选择，并继续进行那些有可能将我们带到解决方案的选择。

根据wiki的定义。

回溯可以被定义为一种通用的算法技术，它考虑搜索每一个可能的组合，以解决一个计算问题。

如何确定一个问题是否可以用回溯法解决？

一般来说，每一个约束满足问题，如果对任何客观的解决方案都有清晰明确的约束，逐步建立一个候选的解决方案，并在确定候选方案不可能完成为一个有效的解决方案时立即放弃该候选方案（"回溯"），都可以用回溯法解决。

然而，所讨论的大多数问题都可以用其他已知的算法来解决，如动态编程或贪婪算法，其时间复杂度按输入大小排序为对数、线性、线性-对数，因此，在各方面都胜过回溯算法（因为回溯算法一般在时间和空间上都是指数级的）。然而，仍然有一些问题，直到现在还只有回溯算法可以解决。

逆向追踪可以被认为是一种选择性的树/图遍历方法。树是代表一些初始起始位置（父节点）和最终目标状态（叶子之一）的方式。逆向追踪使我们能够处理一些情况，在这些情况下，原始的暴力方法会爆发出不可能的选择数量来考虑。逆向追踪是一种精炼的蛮力。在每一个节点上，我们消除那些明显不可能的选择，并继续递归地检查那些有潜力的选择。这样一来，在树的每一个深度，我们都能减少未来要考虑的选择数量。

在回溯中，有三类问题--

决策问题--在这个问题中，我们寻找一个可行的解决方案。

优化问题--在这个问题中，我们寻找最佳解决方案。

枚举问题--在这个问题中，我们要找到所有可行的解决方案。

现在让我们看一下回溯的一些例子。

但在我们开始之前，让我们先看看递归和回溯的区别是什么

在递归中，函数一直在调用自己，直到它达到一个基本情况。在回溯中，我们使用递归来探索所有的可能性，直到我们得到问题的最佳结果。

现在回到正题，让我们从递归开始。

当一个函数调用它自己时，它就被称为递归。对于那些看过电影《盗梦空间》的人来说，这将会更容易。莱昂纳多做了一个梦，在那个梦里他又做了一个梦，在那个梦里他又做了一个梦，如此循环下去。所以这就像有一个叫dream()的函数，而我们只是在本身中调用它。

递归在解决那些可以被分解成同类小问题的问题时很有用。但是，当涉及到使用递归解决问题时，有几件事需要注意。让我们举个简单的例子，试着去理解这些。以下是使用递归寻找一个给定数字X的阶乘的伪代码。

下图显示了阶乘(5)的工作情况。

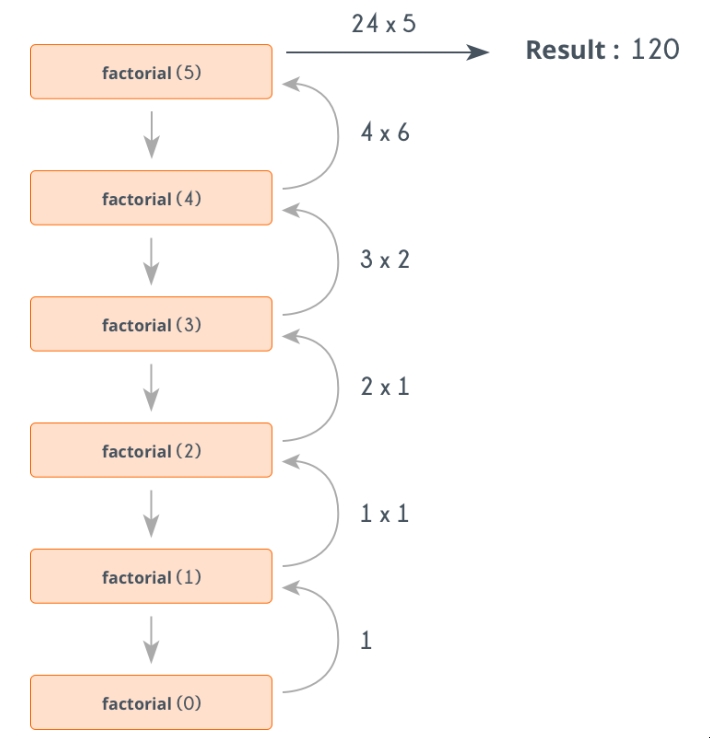
基本情况。任何递归方法都必须有一个终止条件。终止条件是一个已经知道答案的条件，我们只需要返回它。例如，对于阶乘问题，我们知道阶乘(0)=1，所以当x为0时，我们只需返回1，否则我们将分成更小的问题，即找到x-1的阶乘。

如果我们不包含一个基数，函数就会不断调用自己，最终会导致堆栈溢出。例如，上面给出的dream()函数没有基例。如果你用任何语言为它写代码，都会出现运行时错误。

递归调用的数量。递归调用的数量是有上限的。为了防止这种情况，请确保你的基本情况在超过堆栈大小限制之前就达到了。

因此，如果我们想用递归来解决一个问题，那么我们需要确保。

该问题可以分解成相同类型的小问题。 问题有一些基本情况。 在超过堆栈大小的限制之前达到基本情况。 逆向追踪。

因此，在使用递归解决一个问题时，我们将给定的问题分解成更小的问题。假设我们有一个问题A，我们把它分成三个较小的问题B、C和D。现在可能的情况是，A的解决方案并不取决于所有三个子问题，事实上我们甚至不知道它取决于哪一个。

让我们来看看一个情况。假设你站在三条隧道前，其中一条隧道的尽头有一袋黄金，但你不知道是哪一条。所以你就把三个都试一下。首先进入隧道1，如果不是那个，就从里面出来，进入隧道2，如果不是那个，再从里面出来，进入隧道3。因此，基本上在回溯中，我们试图解决一个子问题，如果我们没有达到预期的解决方案，那么就撤销我们为解决该子问题所做的一切，并尝试解决另一个子问题。

让我们来看看一个标准问题。

N-Queens问题：给定一个有N×N个单元格的棋盘，我们需要放置N个皇后，使任何皇后都不会被其他皇后攻击。皇后可以横向、纵向和斜向攻击。

因此，最初我们有N×N个未被攻击的单元格，我们需要放置N个皇后。让我们把第一个皇后放在一个单元格（i,j），所以现在未被攻击的单元格数量减少了，需要放置的皇后数量是N-1。将下一个王后放在某个未被攻击的单元格中。这又减少了未被攻击的单元格的数量，要安置的王后数量变成了N-2。继续这样做，只要以下条件成立。

未被攻击的单元格的数量不是0。

要放置的皇后数量不为0。

如果要放置的皇后数量变成0，那么就结束了，我们找到了一个解决方案。但是如果未被攻击的单元格的数量变成了0，那么我们就需要回溯，也就是说，将最后放置的皇后从当前单元格中移除，并将其放置在其他单元格中。我们递归地做这件事。

下面给出了完整的算法。

is attacked( x, y, board[][], N)
  //checking for row and column 
  if any cell in xth row is 1
    return true
  if any cell in yth column is 1
    return true

  //checking for diagonals
  if any cell (p, q) having p+q = x+y is 1
    return true
  if any cell (p, q) having p-q = x-y is 1
    return true return false

N-Queens( board[][]，N )
  if N is 0//All queens have been placed
    return true 
    
  for i = 1 to N {
    
    
    for j = 1 to n {
    
    
      if is attacked(i, j, board, N) is true
        skip it and move to next cell
      board[i][i] =1
      //Place current queen at cell (i.i)
      
      if N-Queens( board, N-1) is true
      // Solve subproblem
        return true
        // if solution is found 
            return true
        
           board[i][j] = 0
           /* if solution is not found undo whatever changes
          //were made i.e., remove current queen from (i,i)*
      }
  }
  return false

以下是它如何在以下情况下工作

N=4

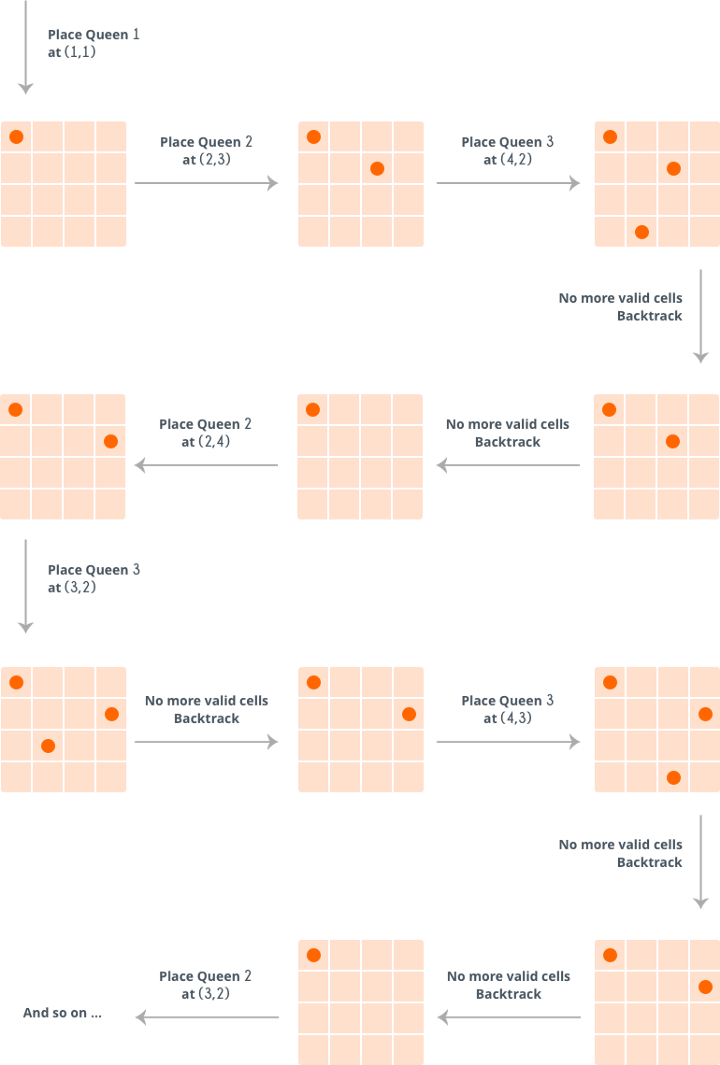
所以，在最后，它达到了以下的解决方案。

所以，很明显，上述算法，尝试解决一个子问题，如果没有得到解决，它就会撤销所做的任何改变，并解决下一个子问题。如果解决方案不存在（N=2），则返回错误。