前言

混个活跃度，本文内容主要为Python版本的树状数组，原理的话，这个不太好阐述（受限于博文篇幅的原因）不过这里还是会尽可能稍微解释一下，它里面的lowbit 操作的。

那么话说回来这个树状数组有什么用呢，其实主要就是为了对付这个区间问题，比如区间修改啥的。那么这些部分的操作有差分，线段树，树状数组啥的，那么今天要说的就是这个树状数组。
那么树状数组解决了哪些问题呢，大概可以解决这三种类型的问题：

1. 区间查询， 单点修改
2. 区间修改， 单点查询
3. 区间修改， 区间查询

那么修改的是啥，查询的是啥呢。首先对于第一类问题，也就是使用树状数组最原始的问题，那么一开始，这个树状数组呢，其实是在平衡前缀和的功能，我们知道前缀和可以快速查询到当前位置i之前的和，这个时间复杂度是O(1) 的，但是当我们的原数组进行修改之后的话，我们的前缀数组就需要进行更新此时操作就是O(n)的，所以的话为了平衡这样的时间消耗，有这个树状数组，他的时间复杂度都是O(nlogn)的。

那么此时再配合差分，这样的话我们就可以实现这个区间修改的功能了。

lowbit操作

数组划分

那么整个树状数组的实现非常简单，那么其中一个比较重要的操作其实就是这个lowbit操作，那么这个操作的话其实和这个树状数组的原理有关。
首先我们知道一个数字（十进制）可以用二进制数字求和表示（我们的计算机就是这样操作的）因此对于一个长度为X的数组，我们可以通过二进制为进行划分。那么这里的话就要扯到这个玩意是如何划分的了：

假设一个数X=2^ki + 2^ki-1 + …+ 2^i
也就是一个数的二进制表示假设是这样的： 0100 1010
我们转换十进制的时候其实就是刚刚的公式
ki,ki-1 表示的都是在这个二进制表示当中为1的地方。

所以我们就可以这样把一个长度为X的区间，划分为(x-2^i, x],（x-2^i - 2^i2,x- 2^i]…
这样划分下去，那么显然lowbit的操作其实就是，找到最后的一个1的那个数b,然后X-b就可以划分出一个区间了。

那么此时我们的这个区间划分好了，我们的目的是为了实现这个区间查询和单点的修改。首先看到区间查询，我们要实现这个区间查询，然后区间被划分，所以的话我们就需要一个东西来记录原数组的值和区间的一个值。

红色的就是我们记录值的区间值的玩意。

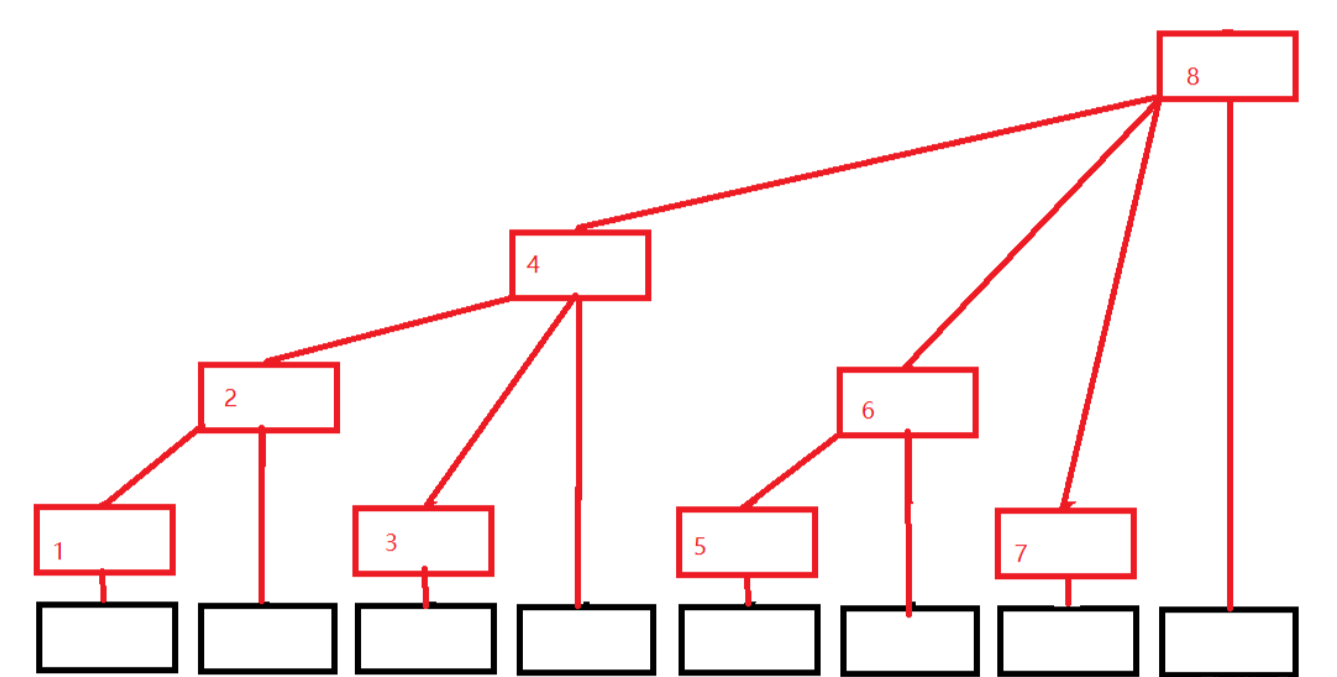
我们用一个大数组来存储区间维护的信息。
那么此时
C[1] = nums[1]
C[2] = C[1]+A[2] = A[1] + A[2]

然后就有个规律：
C[i] = A[i-2^k +1] + …+ A[i]
那么这个k的话就是我们二进制表示里面为1的地方。那么我们的lowbit操作就是这样的，找到这个数（十进制）。

操作

那么现在我们就来看看这个lowbit的操作，这个的话就是这个这个公式：
从位运算的角度我们得到的公式是这样的：

def lowbit(x):
	return x&(~x+1)

然后的话，假设x是正数，~x 得到了x作为负数的反码，之后反码+1得到了-x的补码，然后知道我们的计算机是通过补码运算的，所以的话，我们的函数可以优化为

def lowbit(x);
	return x&(-x)

那么当x为负数的时候 x相当于正数的-x,-x相当于原来正数的x，所以情况是一样的。当然你也可以自己写一遍看看，记住计算机是补码运算就好了。

单点修改，区间查询

ok,我们现在就直接看到代码了，因为代码比较简单，就算你不理解也没关系，你只需要知道怎么用就好了。

class TreeList():

    def __init__(self,nums,maxn=10000):
        self.maxn = maxn
        self.c = [0]*self.maxn
        self.n = len(nums)
        for i in range(1,self.n+1):
            self.update(i,nums[i-1])

    def update(self,i,k):

        while(i<=self.n):
            self.c[i]+=k
            i+=self.lowbit(i)

    def getSum(self,i):
    	# 1~i 之和
        ans = 0
        while(i>0):
            ans += self.c[i]
            i-=self.lowbit(i)
        return ans

    def getSumLR(self,L,R):
        ans = 0
        ans+=self.getSum(R)
        ans-=self.getSum(L-1)
        return ans

    def lowbit(self,x):
        return x&(-x)

区间修改，点单查询

加了个差分数组

class TreeList2():

    def __init__(self,nums,maxn=10000):
        self.maxn = maxn
        self.nums = [0]+nums
        self.c = [0]*self.maxn
        self.n = len(nums)
        self.d = [0]*self.maxn


        for i in range(1,self.n+1):
            self.d[i] = self.nums[i]-self.nums[i-1]
            self.insert(i,self.d[i])

    def insert(self,i,k):

        while(i<=self.n):
            self.c[i]+=k
            i+=self.lowbit(i)
    def update(self,l,r,k):
        self.insert(l,k)
        self.insert(r+1,-k)

    def get(self,i):
        ans = 0
        while(i>0):
            ans += self.c[i]
            i-=self.lowbit(i)
        return ans

    def lowbit(self,x):
        return x&(-x)

区间修改，区间查询

其实这个区间查询当L=R的时候，就是一个单点查询。

class TreeList3():

    def __init__(self,nums,maxn=10000):
        self.maxn = maxn
        self.nums = [0]+nums
        self.c = [0]*self.maxn
        self.n = len(nums)
        self.b = [0]*self.maxn
        for i in range(1,self.n+1):
            self.insert(i,self.nums[i]-self.nums[i-1])

    def insert(self,x,k):
        i = x
        while(i<=self.n):
            self.b[i]+=k
            self.c[i]+=x*k
            i+=self.lowbit(i)

    def update(self,l,r,k):
        self.insert(l,k)
        self.insert(r+1,-k)

    def getSum(self,x):
        ans = 0
        i = x
        while(i>0):
            ans += (x+1)*self.b[i] - self.c[i]
            i-=self.lowbit(i)
        return ans

    def getSumLR(self,L,R):
        ans = self.getSum(R)
        ans -= self.getSum(L-1)
        return ans

    def lowbit(self,x):
        return x&(-x)

总结

ok，上面就是这个本文的内容了，时间关系，我就不说那么多了，没办法，水一水活跃度。