最近那个GPT4是真火,我们现在还很难想象未来人工智能会变成什么样?如果当它们有自己的意识时,我们和它们应该又是一种什么样的关系呢?不解!那就多多学习学习
目录
一.聚类
什么是聚类?我们常说物以类聚,人以群分,这其实也就是聚类最形象的解释。聚类呢,就是按事务的相似性对事务进行分类,它属于无监督学习,是机器学习的入门算法。
这里我们介绍一下聚类算法中比较简单几个算法,以做为进一步学习奠定基础:
- k均值聚类算法
- DBSCAN算法
- OPTICS算法
- AGNES算法
二.k均值聚类算法(k-means)
k均值聚类算法是一种迭代的算法,该算法是对样本集进行分簇,样本的相似性差异我们叫做样本距离,有差异就有距离,然后相似性的比较我们叫做距离度量。k均值聚类算法将样本集进过一系列操作后,让每一个样本点都无限地接近一个簇中心,样本集的分簇个数是我们在开始聚类前指定的,称为k,k均值聚类算法的k由此而来。每一个样本点到本簇的中心的距离的平方和称为误差平方和(SSE)
该算法一般采用欧式距离做为样本距离度量的准则,例如样本点和
的欧式距离定义为:
当采用欧式距离,并以误差平方和SSE做为损失函数时,簇中心计算方法如下:
对于第i个簇,簇中心就是簇内所有点的均值,簇中心第j个特性为,
为样本总数:
SSE计算方法为:dist[*]为距离计算函数,常用欧式距离()表示样本
所在的簇中心
1.k均值聚类算法的流程
k均值聚类算法是按事务的相似性进行分组,流程如下:
- 随机产生k个初始簇中心或者随机选择k个点作为初始簇中心
- 对于每一个样本点,计算它和所有簇的距离,然后将样本点分配到距离最近的簇
- 如果没有点发生分配点结果改变,就结束
- 计算新的簇中心
- 跳到流程2
k-means算法以重新计算簇中心为一个周期,重复流程,直到簇稳定为准,看下图(忽略背景图上的美女):
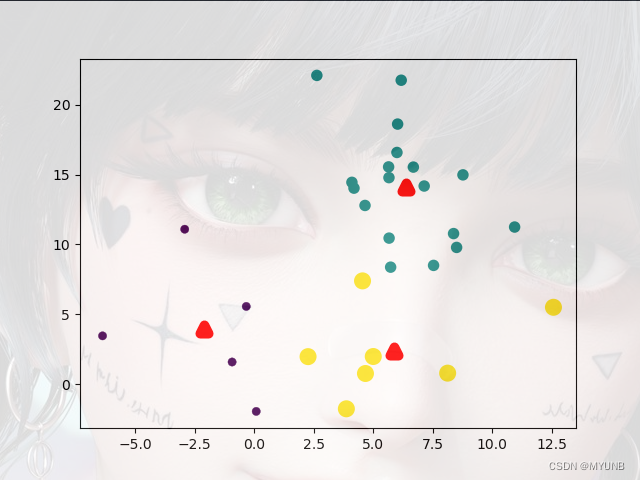
看图,图上的三个红三角是我们事先指定的k,即簇中心,其他点是样本点,我们不断计算每一个样本点到每个红三角簇中心的欧式距离,然后将样本点分配到距离近的簇周变,得到簇稳定后,每一个簇中心边上的样本点就形成了一个相似的集合。黄点在一个区域,绿点和紫点分别在其他区域。如果按我们人的分类,我们可以很轻松地将样本点以不同形状颜色大小进行分类,但机器不行,机器不会区分颜色,看不成形状大小,但,当分簇完成以后,机器就可以按照样本点在不同簇中心周边的分布去判断哪些样本点是一类的或相似的
让我们看看上面这个图的k-means算法实例代码:
import numpy as np
import matplotlib.pyplot as plt
def L2(vecXi, vecXj):
"""
计算欧氏距离
para vecXi:点坐标,向量
para vecXj:点坐标,向量
retrurn: 两点之间的欧氏距离
"""
return np.sqrt(np.sum(np.power(vecXi - vecXj, 2)))
def kMeans(S, k, distMeas=L2):
"""
K均值聚类
para S:样本集,多维数组
para k:簇个数
para distMeas:距离度量函数,默认为欧氏距离计算函数
return sampleTag:一维数组,存储样本对应的簇标记
return clusterCents:一维数组,各簇中心
retrun SSE:误差平方和
"""
m = np.shape(S)[0] # 样本总数
sampleTag = np.zeros(m)
# 随机产生k个初始簇中心
n = np.shape(S)[1] # 样本向量的特征数
clusterCents = np.mat([[-1.93964824, 2.33260803], [7.79822795, 6.72621783], [10.64183154, 0.20088133]])
# clusterCents = np.mat(np.zeros((k,n)))
# for j in range(n):
# minJ = min(S[:,j])
# rangeJ = float(max(S[:,j]) - minJ)
# clusterCents[:,j] = np.mat(minJ + rangeJ * np.random.rand(k,1))
sampleTagChanged = True
SSE = 0.0
while sampleTagChanged: # 如果没有点发生分配结果改变,则结束
sampleTagChanged = False
SSE = 0.0
# 计算每个样本点到各簇中心的距离
for i in range(m):
minD = np.inf
minIndex = -1
for j in range(k):
d = distMeas(clusterCents[j, :], S[i, :])
if d < minD:
minD = d
minIndex = j
if sampleTag[i] != minIndex:
sampleTagChanged = True
sampleTag[i] = minIndex
SSE += minD ** 2
print(clusterCents)
plt.scatter(clusterCents[:, 0].tolist(), clusterCents[:, 1].tolist(), c='r', marker='^', linewidths=7)
plt.scatter(S[:, 0], S[:, 1], c=sampleTag, linewidths=np.power(sampleTag + 0.5, 2))
plt.show()
print(SSE)
# 重新计算簇中心
for i in range(k):
ClustI = S[np.nonzero(sampleTag[:] == i)[0]]
clusterCents[i, :] = np.mean(ClustI, axis=0)
return clusterCents, sampleTag, SSE
if __name__ == '__main__':
samples = np.loadtxt("kmeansSamples.txt")
clusterCents, sampleTag, SSE = kMeans(samples, 3)
# plt.scatter(clusterCents[:,0].tolist(),clusterCents[:,1].tolist(),c='r',marker='^')
# plt.scatter(samples[:,0],samples[:,1],c=sampleTag,linewidths=np.power(sampleTag+0.5, 2))
plt.show()
print(clusterCents)
print(SSE)
当我们运行后:
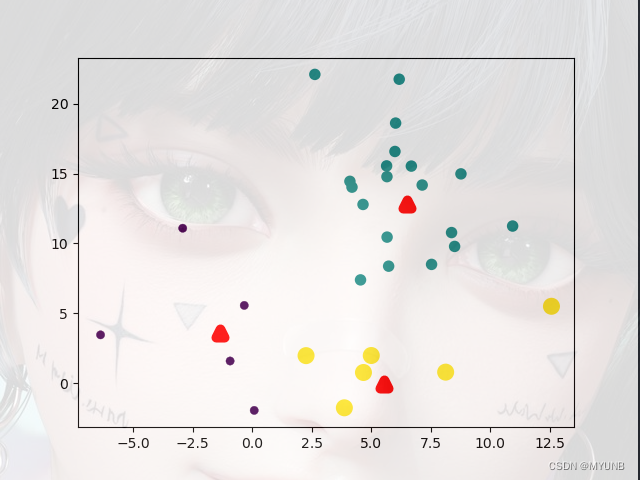
迭代一次
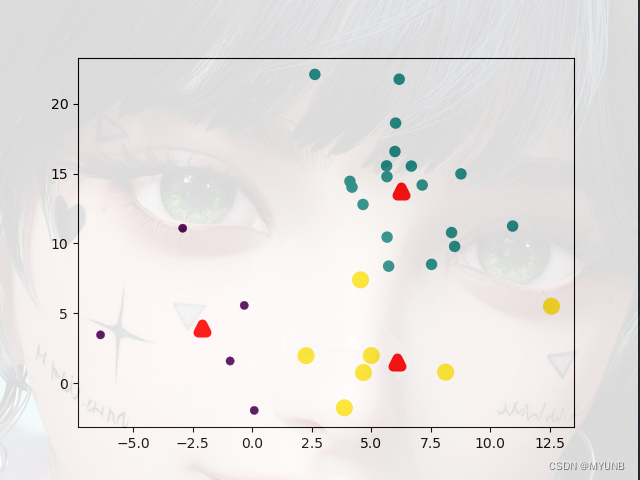
又迭代一次
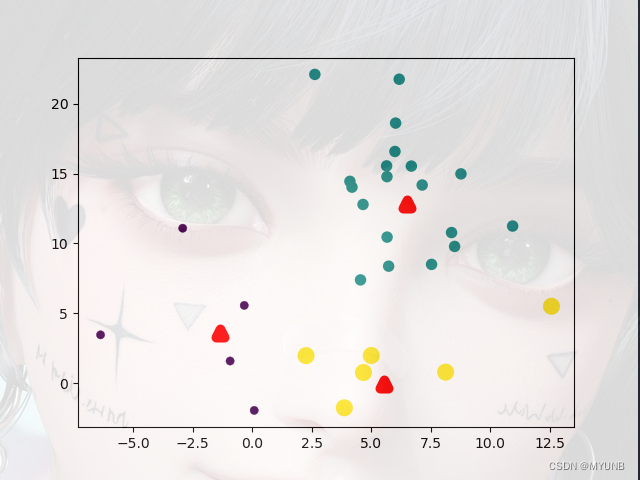
再迭代一次
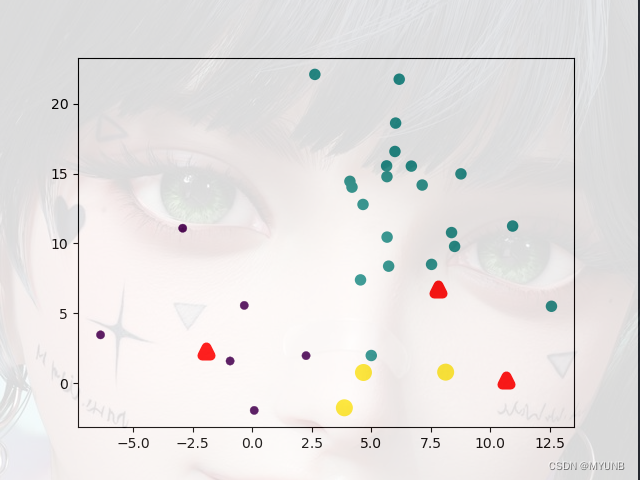
迭代完成,簇趋于稳定
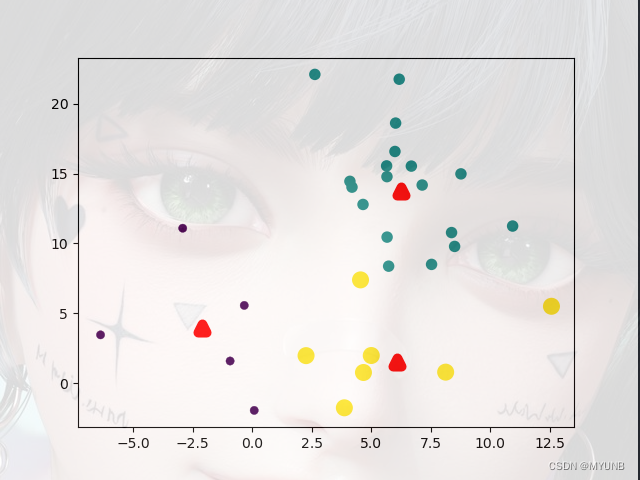
二.k均值算法的改进
k-means算法的初始簇中心是我们事先指定,不同的簇中心会对算法最后的结果产生不可预料的差异,如下是对该算法的一些改进:
1.二分k-means算法
二分k-means算法是为了试图克服k-means算法收敛于局部最优的值,它的算法是先将所有点看出一个簇,然后将簇一分为二,之后在选择其中一个簇继续分裂,具体选择哪个簇继续分裂,要看分裂簇后能否最大限度地降低SSE值,算法流程如下:
- 将所有样本点看成一个簇
- 当簇数量小于k时,进行分裂,计算SSE值,计算减少的SSE值,纪录减少SSE值最多的
- 对分簇减少SSE最多的簇进行分簇,执行2流程
2.k-means++算法
k-means算法也是克服k-means算法收敛于局部最优的值,该算法流程:
- 从样本集中随机取一个点放到簇集合中
- 计算该样本点到簇的距离
- 将样本点到簇的距离转换为概率
- 计算使用样本点的概率,最后按概率将样本点放到簇中,按概率的方法有很多种
3.k-medoids算法
该算法和k-means算法差不多,唯一不同的就是k-medoids算法在产生新簇时不同,k-means算法是采取所有样本点均值来产生簇中心,而k-medoids算法是选取一个样本点为簇中心,选取的标准是所有样本点到该簇中心的距离和最小
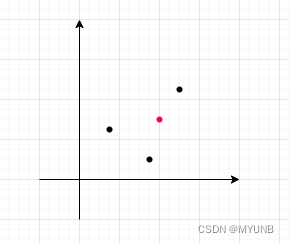
如图,所有样本点到红点的距离和最小,那么红点就是新的簇中心
4.Mini Batch k-means算法
k- medoids算法在样本点和特征量非常大的时候,簇中心的计算量就会非常大,而Mini Batch k-means算法是采取损失质量优化效率的策略来解决这个问题的算法,它的基本思想是随机选取一部分样本点来计算簇中心,计算过程和k-medoids算法一样。
另外几个算法后面下一章介绍!