复数
-
定义
c = a + b i ( a , b ∈ R ) \large {c = a+bi (a,b ∈ R)} c=a+bi(a,b∈R),a为实部,b为虚部,i为虚数单位i 2 = − 1 \large i^2 = -1 i2=−1
-
用矩阵表示复数(仅需实部和虚部)
c = [ a b ] \large \begin{bmatrix} a \\ b\end{bmatrix} \quad [ab] -
复数乘法
c 1 = a + b i c 2 = c + d i c 3 = c 1 c 2 = ( a + b i ) ( c + d i ) = a c + a d i + b c i + b d i 2 = a c − b d + ( a d + b c ) i \large\displaystyle c_1 = a + bi \\ c_2 = c +di\\ c_3 = c_1c_2=(a+bi)(c+di) = ac+adi+bci+bdi^2=ac-bd+(ad+bc)i c1=a+bic2=c+dic3=c1c2=(a+bi)(c+di)=ac+adi+bci+bdi2=ac−bd+(ad+bc)i -
对应的矩阵乘法(可以看到与上面结果一致)
c 1 c 2 = [ a − b b a ] [ c d ] = [ a c − b d b c + a d ] \large \displaystyle c_1c_2 = \begin{bmatrix}a&-b\\b&a\end{bmatrix}\begin{bmatrix} c\\d\end{bmatrix}=\begin{bmatrix} ac-bd \\ bc+ad\end{bmatrix} c1c2=[ab−ba][cd]=[ac−bdbc+ad]
四元数(Quaternion)
-
定义:就是复数的拓展,虚部从1个变为3个
- q = a + b i + c j + d k ( a , b , c , d ∈ R ) \large q = a + bi+ cj + dk (a,b,c,d∈R) q=a+bi+cj+dk(a,b,c,d∈R)
- i 2 = j 2 = k 2 = i j k = − 1 \large i^2 = j^2 = k^2 = ijk = -1 i2=j2=k2=ijk=−1
- i j = k , j k = i , k i = j \color{red}{ij=k,jk=i,ki=j} ij=k,jk=i,ki=j *(前两个相乘等于后一个)
-
四元数的表示
- 1个实数+1个向量(向量由3个虚部组成)
- q = ( a , v ) , ( v = [ b c d ] ) \large q = (a,v),(v = \begin{bmatrix}b\\c\\d\end{bmatrix}) q=(a,v),(v= bcd )
-
四元数乘法运算
q 1 = a + b i + c j + d k \large q_1 = a+bi+cj+dk q1=a+bi+cj+dk
q 2 = e + f i + g j + h k \large q_2 = e+fi+gj+hk q2=e+fi+gj+hk
q 1 q 2 = [ a − b − c − d b a − d c c d a − b d − c b a ] [ e f g h ] \large \displaystyle q_1q_2=\begin{bmatrix}a&-b&-c&-d\\b&a&-d&c\\c&d&a&-b\\d&-c&b&a\end{bmatrix}\begin{bmatrix} e\\f\\g\\h\end{bmatrix} q1q2= abcd−bad−c−c−dab−dc−ba efgh 乘法运算其实就是两个向量的乘法,最终ijk都被消掉了
-
四元数的模
∣ ∣ q ∣ ∣ = a 2 + b 2 + c 2 + d 2 \large ||q|| = \sqrt{a^2+b^2+c^2+d^2} ∣∣q∣∣=a2+b2+c2+d2 -
共轭四元数
q ∗ = a − b i − c j − d k \large q^* = a-bi-cj-dk q∗=a−bi−cj−dk -
互逆性
q − 1 q = q q − 1 = 1 \large q^{-1}q = qq^{-1}=1 q−1q=qq−1=1
四元数旋转的计算
-
空间中一个向量 v = ( b , c , d ) T \large v =(b,c,d)^T v=(b,c,d)T,对其进行旋转,这个旋转运动用四元数表示为q = (a,b,c,d) ,||q|| = 1
-
先把空间中的向量变成四元数形式,实部为0,3个分量对应四元数的3个虚部
v q = ( 0 , v ) = 0 + b i + c j + d k \large v_q =(0,v)=0 + bi+cj+dk vq=(0,v)=0+bi+cj+dk -
对向量 v q v_q vq做旋转运算,即在其两边分别乘上q和q的逆
v q ′ = q v q q ∗ = q v q q − 1 \large v'_q =qv_qq^*=qv_qq^{-1} vq′=qvqq∗=qvqq−1 -
最终,任何一个空间中的点或者向量的旋转都能表示成一个3x3的矩阵与之相乘
v ′ = [ 1 − 2 c 2 − 2 d 2 2 b c − 2 a d 2 a c + 2 b d 2 b c + 2 a d 1 − 2 b 2 − 2 d 2 2 c d − 2 a b 2 b d − 2 a c 2 a b + 2 c d 1 − 2 b 2 − 2 c 2 ] ⋅ v \large v'=\begin{bmatrix} 1-2c^2-2d^2&2bc-2ad&2ac+2bd\\2bc+2ad&1-2b^2-2d^2&2cd-2ab\\2bd-2ac&2ab+2cd&1-2b^2-2c^2\end{bmatrix}·v v′= 1−2c2−2d22bc+2ad2bd−2ac2bc−2ad1−2b2−2d22ab+2cd2ac+2bd2cd−2ab1−2b2−2c2 ⋅v
-
-
q的反向旋转(求逆)
q − 1 = q ∗ ∣ ∣ q ∣ ∣ 2 \large q^{-1} = \Large \frac{q^*}{||q||^2} q−1=∣∣q∣∣2q∗,如果是标准化后的四元数(模为1),则q的逆就等于其共轭四元数,即虚部取反即可 -
多个旋转的组合
v ′ ′ = q 2 q 1 v q 1 ∗ q 2 ∗ = ( q 2 q 1 ) v ( q 2 ∗ q 1 ∗ ) ∗ \large v'' = q_2q_1vq^*_1q^*_2 =(q_2q_1)v(q^*_2q^*_1)^* v′′=q2q1vq1∗q2∗=(q2q1)v(q2∗q1∗)∗,其实基本跟矩阵的运算法则相同四元数用向量表示后,满足向量运算法则
-
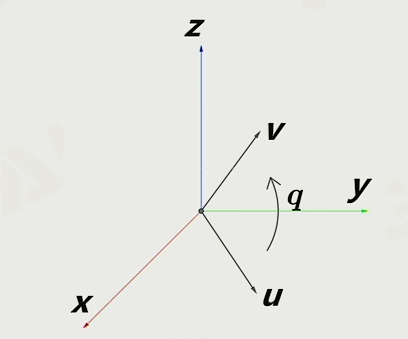
已知两个单位向量,求旋转四元数q( 从u到v的旋转)
- 先用叉乘求出平面uv的法向量: w = u × v \large \mathbf w = u \times v w=u×v
- 用四元数表示旋转: q = [ u ⋅ v + ( w ⋅ w ) + ( u ⋅ v ) 2 , w . x , w . y , w . z ) ] \large \mathbf q =[u·v+\sqrt{(w·w)+(u·v)^2}, w.x, w.y, w.z)] q=[u⋅v+(w⋅w)+(u⋅v)2,w.x,w.y,w.z)]
-
绕任意给定轴的旋转
- 给定一个轴(x,y,z)和旋转角度θ
- q = ( c o s ( θ / 2 ) , s i n ( θ / 2 ) x u , s i n ( θ / 2 ) y u , s i n ( θ / 2 ) z u ) \Large q=(cos(\theta/2), sin(\theta/2)x_u, sin(\theta/2)y_u,sin(\theta/2)z_u) q=(cos(θ/2),sin(θ/2)xu,sin(θ/2)yu,sin(θ/2)zu)
- 旋转乘法: v q ′ = q v q q ∗ = q v q q − 1 \large v'_q = qv_qq^* = qv_qq^{-1} vq′=qvqq∗=qvqq−1