随机位生成和流密码
在对称密码的最后,介绍关于流密码的一些知识。与分组密码不同,流密码每次仅仅加密数据流的1位或1字节,加密的密钥常常由密钥生成算法产生,尽管流密码不如分组密码能够高效地加/解密,但流密码依旧有很广阔的用途,其适合于加密大量的快速数据流,并且适合在内存和处理能力非常有限的设备中使用,因此学习流密码仍然有重要的意义。
更新历史:
- 2021年08月22日完成初稿
1. 随机位生成
随机位生成是指生成具有随机性的随机位流,随机位流广泛用于密钥生成和加密。现实中,往往有两种随机位生成策略:
- 伪随机数生成器(Pseudo Random Number Generator, PRNG),也称确定性随机位生成器(Deterministic Random Bit Generator, DRBG),伪随机数生成器利用算法确定性地计算产生随机位。
- 真随机数生成器(True Random Number Generator, TRNG),也称非确定性随机位生成器(Non-Deterministic Random Bit Generator, NRBG),真随机数生成器使用某种物理源生成非确定性的随机位,这种物理源能够产生某些类型的随机输出。
尽管两种随机数生成器有所区别,但其目标是一致的,那就是产生一组随机数。对于随机数而言,一般要满足以下两点要求:
- 随机性:即在某种明确定义的统计意义下,数序列是随机的,通常有以下两个评价标准:
- 分布均匀性:生成的随机数序列应是均匀的,即0和1出现的概率大致相等
- 独立性:序列中的任何子序列都不能由其他子序列推导出来
- 不可预测性:随机数中的任何一部分都不能通过预测得出正确结果,即预测结果是无效的
往往真随机数满足以上两点要求,因此真随机数是想要的结果,但是在下面的讲述中可以发现真随机数并不够高效,因此也就有了伪随机数。人们总是希望高效产生一组伪随机数,让这组伪随机数具有上述真随机数的完美性质,下面就针对这两种随机数进行介绍。
1.1 伪随机数
在现实应用中,往往采用密码算法产生随机数,这类随机数称为伪随机数。由于它们是由密码算法得出,有些情况不能满足随机性和不可预测性,因此不全是真正的随机数。下面就介绍一下目前生成伪随机数的原理和一些生成方案。
1.1.1 伪随机数生成的原理
图1.1介绍了两个伪随机数生成器(PRNG、PRF)。
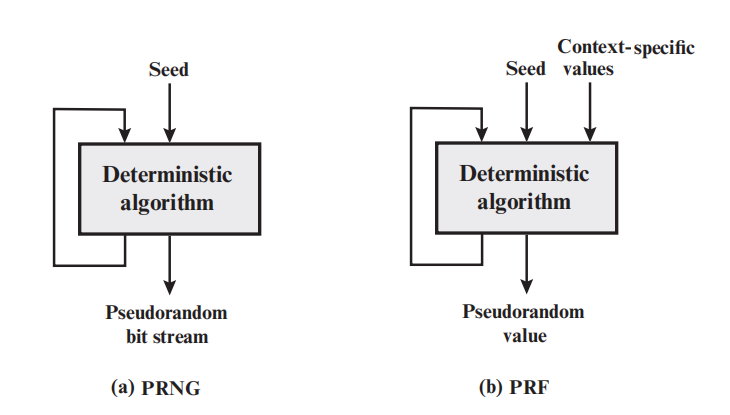
对于伪随机数生成器(PRNG),通常会取一个种子(seed)作为输入,而且还会有之前产生的输出序列作为输入,然后通过确定性算法(Deterministic algorithm)产生伪随机位流(Pseudorandom bit stream)。通常而言,种子由真随机数生成器(TRNG,在1.2节会具体介绍)产生,因此种子值往往是随机的。另外,之前产生的输出序列会作为输入,因此之前产生的输出序列会影响之后的输出。
而对于伪随机数函数(Pseudo Random Function, PRF),事实上其和伪随机数生成器(PRNG)很类似,两者的区别如下:
- 伪随机数生成器(PRNG):用于生成不限长位序列,比如生成对称流密码的输入
- 伪随机函数(PRF):用于生成固定长度的伪随机串,比如对称密码的密钥和时变值
除此之外,两者几乎没有什么差别,其目的都是生成具有随机性和不可预测性的伪随机位流,在文章中也不区分伪随机数生成器(PRNG)和伪随机数函数(PRF),因此两种生成器也统称为PRNG。
1.1.2 伪随机数生成
在介绍如何生成伪随机数之前,先介绍一下伪随机数如何才能被接受作为随机数,前述中提出了随机性和不可预测性两大要求,下面针对这两点要求作进一步阐述。
对于伪随机数生成器(PRNG)和伪随机数函数(PRF)而言,设计者往往要求不知道种子(seed)的敌手无法确定伪随机串,因此对PRNG和PRF有以下三方面的要求:
- 随机性
- 均匀性:在生成随机或伪随机位序列的任何位置,0或1出现的次数大致相等
- 可伸缩性:若一个序列是随机的,那么其子序列也应是随机的
- 一致性:对于所有初始值(种子),生成器的性质必须是一致性的
- 不可预测性
- 正向不可预测性:若不知道种子,无论知道序列中签前面的多少位都无法预测序列中的下一位
- 反向不可预测性:由随机数序列无法推算到种子值,因此种子和其产生的随机数序列是完全独立的
- 种子的要求:种子值必须是安全的并且不可预测,一般而言,种子本身必须是随机数或伪随机数
在实际密码应用中,往往提供了随机性测试和不可预测性测试,只有通过测试的随机数序列才能被认为是随机数序列。下面就开始介绍常用的几种生成随机数的方法。
1.1.2.1 线性同余生成器
线性同余生成器是一种简单但使用广泛的生成伪随机数的技术,随机数序列 { X n } \{X_n\} {
Xn}由如下公式推导而来:
X n + 1 = ( a X n + c ) m o d m X_{n+1}=(aX_n+c)\;mod\;m Xn+1=(aXn+c)modm
其中 a a a称为乘数( 0 < a < m 0< a< m 0<a<m), c c c称为增量( 0 ≤ c < m 0\le c< m 0≤c<m), m m m称为模数( m > 0 m>0 m>0)。另外,该随机数序列还需要一个初始值(也可称为种子) X 0 X_0 X0( 0 ≤ X 0 < m 0\le X_0<m 0≤X0<m)。
线性同余生成器十分简单,而且当乘数 a a a和模数 m m m选择得好的话,其产生的随机数序列在统计上几乎是完全随机的。可以证明,如果 m m m是素数且 c = 0 c=0 c=0时,对于 a a a的某些值,生成函数的周期为 m − 1 m-1 m−1,但是会缺少0这个值。在一些实际的应用中, m = 2 31 − 1 , a = 7 5 m=2^{31}-1, a=7^5 m=231−1,a=75,此时可以得到比较好的伪随机数序列。
然而,线性同余生成器生成的并不是真正的随机数,在敌手得知各个参数( a , c , m a, c, m a,c,m)和 X 0 X_0 X0后可以很轻松地还原整个序列,更为致命的是,线性同余算法中的参数 a , c , m a, c, m a,c,m可以通过连续的几个值(如 X 0 , X 1 , X 2 , X 3 X_0,X_1, X_2, X_3 X0,X1,X2,X3)推算得出:
X 1 = ( a X 0 + c ) m o d m X 2 = ( a X 1 + c ) m o d m X 3 = ( a X 2 + c ) m o d m X_{1}=(aX_0+c)\;mod\;m\\ X_{2}=(aX_1+c)\;mod\;m\\ X_{3}=(aX_2+c)\;mod\;m X1=(aX0+c)modmX2=(aX1+c)modmX3=(aX2+c)modm
因此,针对线性同余算法,人们提出几种修正的方法,比如每隔N个数就采用新的种子值(如时钟值 X m o d m X\;mod\;m Xmodm)来重启序列。
1.1.2.2 BBS生成器
Blum Blum Shub(BBS)生成器也是常见的生成安全伪随机数的方法,其以开发人员的名字命名。其主要的过程如下:
- 选择两个大素数 p p p和 q q q,其满足 p ≡ q ≡ 3 ( m o d 4 ) p\equiv q\equiv 3(mod\;4) p≡q≡3(mod4)
- 令 n = p × q n=p\times q n=p×q,选择一个随机数 s s s,且 s s s与 n n n互素,最后按照下面的算法来生成位序列
X 0 = s 2 m o d n f o r i = 1 t o ∞ X i = ( X i − 1 ) 2 m o d n B i = X i m o d 2 X_0 = s^2\;mod\;n \\ for\quad i = 1\;to\;\infty \\ \quad\quad\quad\quad\quad X_i=(X_{i-1})^2\;mod\;n\\ \quad\quad\quad B_i = X_i\;mod\;2 X0=s2modnfori=1to∞Xi=(Xi−1)2modnBi=Ximod2
可以证明,BBS生成器的安全性是基于对大整数n的因子分解困难问题的,因此其被称为密码安全伪随机位生成器(CSPRBG)。并不是所有的伪随机数生成器都是CSPRBG,CSPRBG被定义为能够通过下一位测试的伪随机位生成器,所谓的下一位测试指某个伪随机数生成器中的下一位无法通过一个多项式时间算法进行预测,即对于输出序列的前k位输入来说,正确预测第k+1位的概率为0.5。
1.1.2.3 用分组密码生成随机数
除了上述提到的伪随机数生成器,还可以利用分组密码来生成随机数,即使用对称分组密码作为PRNG机制的核心。在之前讲述的分组密码工作模式中,广泛使用的是CTR模式和OFB模式,图1.2展示了这两种情形。
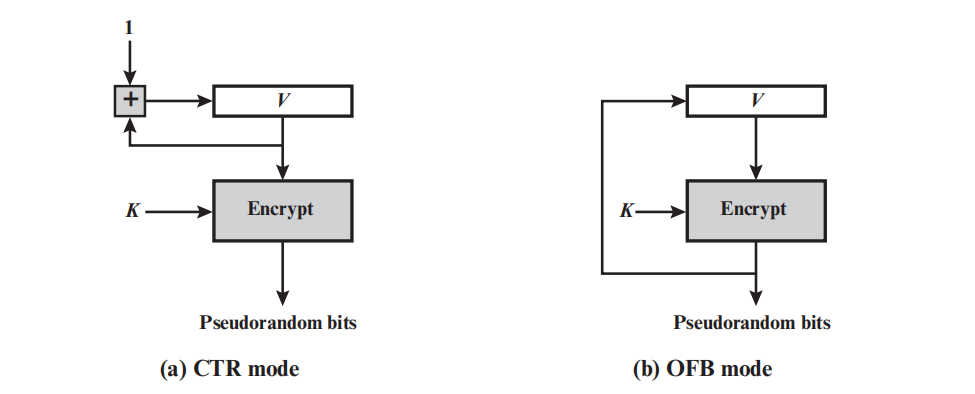
图中的K为加密密钥,V为变量值,每次生成一个伪随机数分组后都将更新V值(如图1.2所示),K和V构成了两种随机数生成器的种子(seed)。
用于PRNG的CTR算法有:
while (len(temp) < requested_number_of_bits) do
V = (V + 1) mod 2^128
output_block = E(key, V)
temp = temp||output_block
用于PRNG的OFB算法总结如下:
while (len(temp) < requested_number_of_bits) do
V = E(key, V)
temp = temp||V
在实际应用中,上述CTR算法和OFB算法的结构都是具体PRNG结构的核心,具体可参考NIST CTR_DRBG(计数器模式确定性随机位生成器)。
1.2 真随机数
正如图1.3所示,真随机数生成器(TRNG)使用熵源作为输入,并将其转换为二进制数,从而得到随机位流。

可以看到真随机数的生成关键在于熵源,熵源本质上是从计算机的物理环境抽取的不确定源,比如键盘敲击时序模式、磁盘点活动、鼠标移动和系统时钟的瞬时值。这些大多数操作都是通过度量不可预测的自然过程进行的,如电离辐射事件的脉冲检测器、气体放电管和泄漏电容器。Intel公司就开发了一种商用的芯片,该芯片可以通过一对反相器的输出进行采样从而实现对热噪声的采样。
由于生成器的输入是真随机源,是不可预测的,因此生成器的输出也具有这种特性,因此产生的随机位流是真正随机的序列。
1.3 PRNG和TRNG的比较
综上所示,可以将真随机数生成器(TRNG)看成真正产生随机数序列的生成器,而伪随机数生成器(PRNG、PRF)则是利用一段较小的真随机数产生的伪随机数序列。显然,读者会认为TRNG是远远优于PRNG、PRF的,但是考虑到下面几个原因,情况就有所不同了:
- 对于流密码而言,明文和密钥是等长的,因此TRNG需要产生和明文一样长的伪随机序列,这就需要十分庞大的熵源。而对于PRNG,其密钥可以由真随机数作为初始密钥,利用密钥生成算法产生实际的加密密钥,因此这是十分高效的。
- 另外,对于使用熵源的TRNG而言,其可能会产生存储偏差的二进制序列,也即不完全随机的二进制序列(而且这是难以控制的)
另外,经常比较TRNG和PRNG的性质还有确定性或不确定性,确定性是指若已知序列的初始值和某些参数(如种子)可以在之后复现某个随机数序列。PRNG使用算法来产生随机数序列,当初始值确定后,使用相同的算法及算法输入便可以产生相同的随机数序列,而TRNG则使用不可预测的熵源来产生随机数序列,由于熵源本身就不可预测,更不能重复上一次使用的熵源,因此TRNG往往是不确定性的。当实际应用中,需要利用到之前产生的随机数序列,那具有确定性是很方便的。
当然,真随机数生成器(TRNG)也有好的性质,比如没有周期性,而伪随机数生成器(PRNG)往往具有周期性,周期性不是一个很好的性质,因为序列的周期性可以让敌手预测序列的下一位,从而使得序列失去随机性。当时伪随机数生成器(PRNG)的周期往往很大,比如 2 32 , 2 64 2^{32},2^{64} 232,264等,这对实际应用来说是可以忽略不计的。
综合上面的讨论,两者的区别总结如下:
| 效率 | 确定性/不确定性 | 周期性 | |
|---|---|---|---|
| 真随机数生成器(TRNG) | 效率低下,生成数字时间较长 | 不确定性 | 没有周期性 |
| 伪随机数生成器(PRNG、PRF) | 效率高,短时间可生成多位数字 | 确定性 | 通常具有周期性 |
2. 流密码
正如前述,和分组密码相比,流密码一次处理较少的分组,比如一位或者一字节,适合于加密大量的快速数据流,并且适合在内存和处理能力非常有限的设备中使用,下面就简单介绍一下流密码的典型结构和常用的流密码。
2.1 流密码典型结构
图2.1展示了典型流密码的结构图,其中 p i , c i p_i, c_i pi,ci是明文和密文, z i z_i zi是密钥流。流密码以初始密钥K和初始变量IV为输入,最终输出密钥流 z i z_i zi,在函数内部,其中 s i s_i si是加密和解密过程中随时间演化的秘密状态,其初始状态被指定为 s 0 s_0 s0; f f f是更新状态的函数,在生成一位时,由旧状态值计算出新状态值; g g g则是密钥流生成函数,其会生成密钥流 z i z_i zi。

可以看到,流密码很类似于一次一密: c i = p i ⊕ k i c_i=p_i\oplus k_i ci=pi⊕ki,不过一次一密使用真随机流密钥,而流密码实际上采用的是伪随机数流密钥,但是使用流密码过程中,要保证伪随机数序列周期足够长、满足随机性和不可预测性,否则流密码并不安全。下面就介绍一下实际中常用的流密码。
2.2 RC4
RC4是Ron Rivest于1987年为RSA Security设计的流密码,是面向字节运算的变长密钥流密码。RC4流密码结构十分简单,其主要有以下两个过程:
- 初始化状态向量S:状态向量S是一个有256字节的数组
- 密钥流生成:利用状态向量S不断生成一个字节密钥流k,该密钥流可以用于加密和解密
首先,RC4有长度为keylen字节的密钥K(如keylen=256),利用该密钥来初始化状态向量:一开始简单对S进行赋值,同时计算临时向量T,之后对S进行置换,最后得到0~255的一个置换S。得到初始化向量S之后,便不再使用密钥K。
/* Initialization */
for i = 0 to 255 do
s[i] = i ;
T[i] = K[i mod keylen] ;
/* Initial Permutation of S */
j = 0 ;
for i = 0 to 255 do
j = (j + S[i] + K[i]) mod 256 ;
swap(S[i], S[j]) ;
接下来便要产生密钥流,其算法如下,算法输出状态向量S的一位,即为密钥流k(一个字节),该密钥流会和明文异或产生密文,或与密文异或产生明文。
/* Stream Generation */
i, j = 0 ;
while(True)
i = (i + 1) mod 256 ;
j = (j + S[i]) mod 256 ;
swap(S[i], S[j]) ;
t = (S[i] + S[j]) mod 256 ;
k = S[t]
对RC4的分析表明,该密码的周期可能完全大于 1 0 100 10^{100} 10100,而且该密码可在软件中快速地运行。不过在最近,RC4密钥调度算法被发现有漏洞,该漏洞可以减少密钥的工作量,从而使得RC4在一些应用中被禁止使用。
2.3 使用反馈移位寄存器的流密码
在现实应用中,随着越来越多的受限设备(如物联网中使用的设备)被人们使用,人们对开发占用最少内存、高效且功耗要求最低的新型流密码的兴趣高涨,因此最近开发的大多数流密码都基于反馈移位寄存器(Feddback Shift Register, FSR)。
图2.2展示了反馈移位寄存器的基本结构,其中方框代表一位的存储单元,存储1bit的 B n − 1 , B n − 2 , . . . , B 1 , B 0 B_{n-1}, B_{n-2},...,B_1,B_0 Bn−1,Bn−2,...,B1,B0。每个单元都有一个输出线和输入线,其中输出线指示当前存储的值(图中为方框内的值),在离散时刻(称为时钟时间),每个存储单元中的值被替换为输入线指示的值。
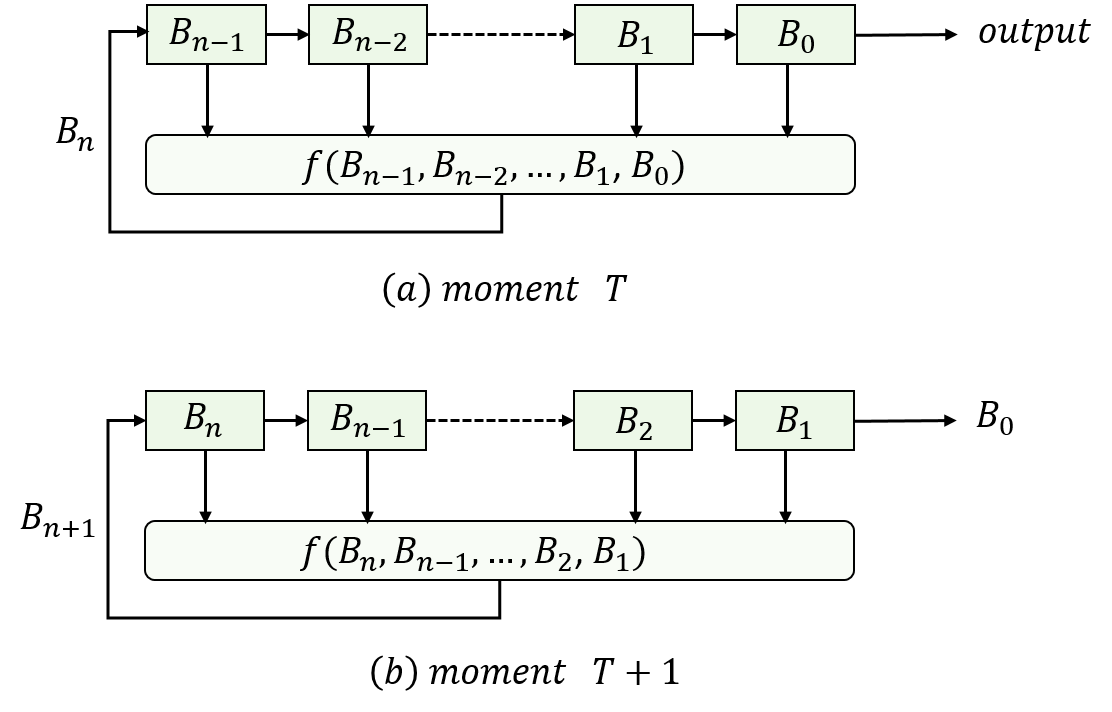
因此在某个时刻T,从左到右第一个存储单元的值为 B n − 1 B_{n-1} Bn−1,第二个存储单元的值为 B n − 2 B_{n-2} Bn−2,依次类推,最后一个存储单元的值为 B 0 B_0 B0;在下一时刻T+1, B n − 1 B_{n-1} Bn−1被 B n B_{n} Bn代替, B n − 2 B_{n-2} Bn−2被 B n − 1 B_{n-1} Bn−1代替,…, B 0 B_{0} B0被 B 1 B_{1} B1代替,最后输出 B 0 B_0 B0,依次类推从而输出 B 0 , B 1 , . . . , B n − 2 , B n − 1 , . . . B_0,B_1,...,B_{n-2}, B_{n-1},... B0,B1,...,Bn−2,Bn−1,...。其基本公式为:
B n = f ( B n − 1 , B n − 2 , . . . , B 1 , B 0 ) B_n = f(B_{n-1}, B_{n-2},...,B_1,B_0) Bn=f(Bn−1,Bn−2,...,B1,B0)
关于反馈移位寄存器(FSR)很重要的一点在于其产生的随机数序列的统计特性有比较完善的理论结果,而且可以通过选择反馈函数 f f f来获得控制序列的周期性,从而使得随机数序列更具有周期性。反馈移位寄存器(FSR)主要有两种:
- 线性反馈移位寄存器(Linear Feedback Shift Register, LFSR)
- 非线性反馈移位寄存器(Non-linear Feedback Shift Register, NFSR)
下列就简单地介绍LFSR和NFSR。
2.3.1 线性反馈移位寄存器
线性反馈移位寄存器(Linear Feedback Shift Register, LFSR)中使用的反馈函数是线性的,即 f f f满足 f ( x + y ) = f ( x ) + f ( y ) f(x+y)=f(x)+f(y) f(x+y)=f(x)+f(y)且 a f ( x ) = f ( a x ) af(x)=f(ax) af(x)=f(ax)。为使得反馈函数具有线性性质,反馈函数中的运算通常仅涉及寄存器中位的模2加运算(即异或运算),此时的反馈移位寄存器( FSR)是线性反馈移位寄存器(LFSR)。定义LFSR有两种模式:
- 使用反馈函数定义:比较直观,但计算量较大
- 使用特征多项式定义:不那么直观,但更有用
下面就介绍两种模式。
2.3.1.1 反馈函数
使用反馈函数时,反馈函数是一个异或求和公式:
f ( B n − 1 , B n − 2 , . . . , B 1 , B 0 ) = A 1 B n − 1 ⊕ A 2 B n − 2 ⊕ . . . ⊕ A n B 0 = ∑ i = 1 n A i B n − i f(B_{n-1}, B_{n-2},...,B_1,B_0) = A_1B_{n-1}\oplus A_2B_{n-2}\oplus ...\oplus A_nB_0=\sum_{i=1}^n{A_iB_{n-i}} f(Bn−1,Bn−2,...,B1,B0)=A1Bn−1⊕A2Bn−2⊕...⊕AnB0=i=1∑nAiBn−i
其中 A 1 , A 2 , . . . , A n A_1, A_2,...,A_n A1,A2,...,An是系数,取值均为 A i ∈ { 0 , 1 } A_i\in\{0,1\} Ai∈{ 0,1},考虑到 B n − i ∈ { 0 , 1 } B_{n-i}\in\{0,1\} Bn−i∈{ 0,1}, A i B n − i A_iB_{n-i} AiBn−i当且仅当 A i = 1 , B n − i = 1 A_i=1, B_{n-i}=1 Ai=1,Bn−i=1时才为1,其余情况均为0,故 A i B n − i A_iB_{n-i} AiBn−i相当于 A i A_i Ai和 B n − i B_{n-i} Bn−i作与运算。 B n − 1 , B n − 2 , . . . , B 1 , B 0 B_{n-1}, B_{n-2},...,B_1,B_0 Bn−1,Bn−2,...,B1,B0就是初始的序列值,序列的下一位即为 B n = f ( B n − 1 , B n − 2 , . . . , B 1 , B 0 ) B_n = f(B_{n-1}, B_{n-2},...,B_1,B_0) Bn=f(Bn−1,Bn−2,...,B1,B0),图2.3就表示了这一关系。
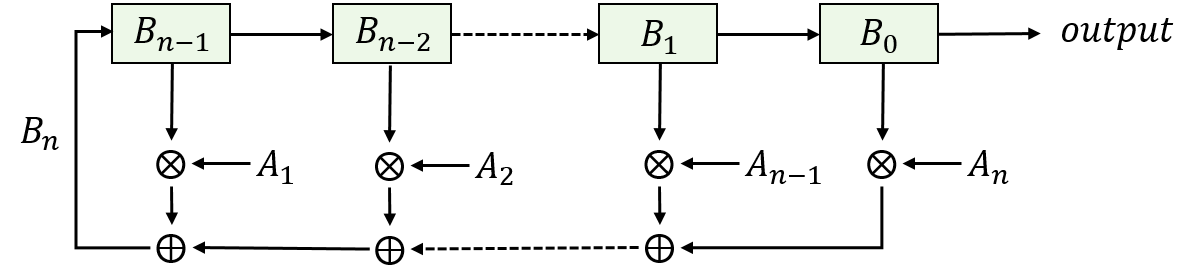
其中, ⊗ \otimes ⊗是逻辑与,则 A i B n − i = A i ⊗ B n − i A_iB_{n-i}=A_i\otimes B_{n-i} AiBn−i=Ai⊗Bn−i,事实上 A i A_i Ai就像一个开关,控制着反馈函数中是否有 B n − i B_{n-i} Bn−i参与运算。
可以证明,上述模式的反馈函数是线性的,称为二进制线性反馈移位寄存器。不过该LFSR是有周期性的,n位的LFSR的周期最大为 N = 2 n − 1 N=2^n-1 N=2n−1,而且总可以找到至少一个反馈函数使得周期达到最大,此时产生的序列称为最大长度序列或m序列。
下面来看一个例子,假设n=4,反馈函数为
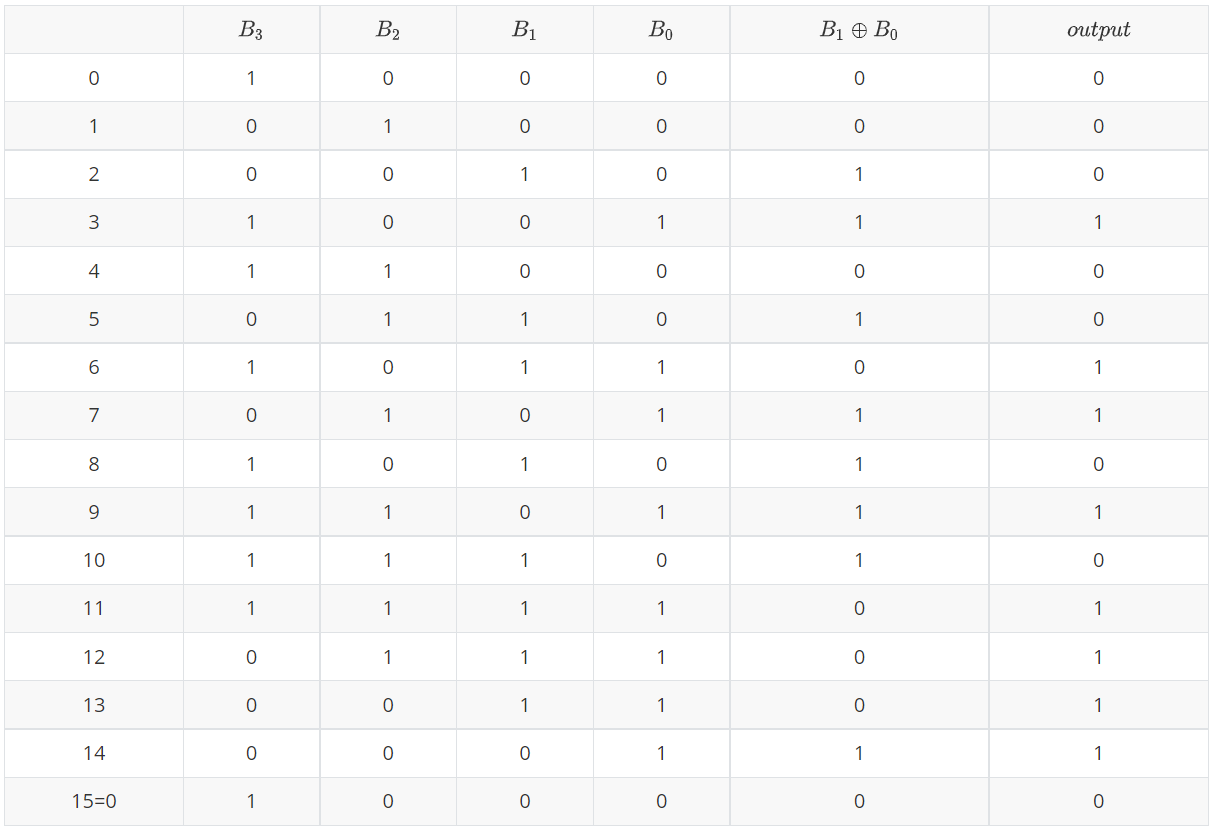
f ( B 3 , B 2 , B 1 , B 0 ) = B 1 ⊕ B 0 = B 4 f(B_3,B_2,B_1,B_0) = B_1\oplus B_0=B_4 f(B3,B2,B1,B0)=B1⊕B0=B4
且初始值 B 3 = 1 , B 2 = 0 , B 1 = 0 , B 0 = 0 B_3=1,B_2=0,B_1=0,B_0=0 B3=1,B2=0,B1=0,B0=0,则有下面的输出序列:0001001101011110,其周期达到了 15 = 2 4 − 1 15=2^4-1 15=24−1,是4位线性反馈移位寄存器的最大的周期。
2.3.1.2 特征多项式
LFSR另一种定义是利用特征多项式,对应于反馈函数:
f ( B n − 1 , B n − 2 , . . . , B 1 , B 0 ) = A 1 B n − 1 ⊕ A 2 B n − 2 ⊕ . . . ⊕ A n B 0 f(B_{n-1}, B_{n-2},...,B_1,B_0) = A_1B_{n-1}\oplus A_2B_{n-2}\oplus ...\oplus A_nB_0 f(Bn−1,Bn−2,...,B1,B0)=A1Bn−1⊕A2Bn−2⊕...⊕AnB0
的特征多项式为:
P ( X ) = 1 + A 1 X + A 2 X 2 + . . . + A n − 1 X n − 1 + A n X n = 1 + ∑ i = 1 n A i X i P(X) = 1+A_1X+A_2X^2+...+A_{n-1}X^{n-1}+A_{n}X^{n}=1+\sum_{i=1}^n{A_iX^i} P(X)=1+A1X+A2X2+...+An−1Xn−1+AnXn=1+i=1∑nAiXi
特征多项式一个很有用的性质是,取多项式的倒数后便用来查找由对应LFSR生成的序列。例如对于反馈函数:
f ( B 2 , B 1 , B 0 ) = B 2 ⊕ B 0 f(B_2, B_1,B_0) = B_2\oplus B_0 f(B2,B1,B0)=B2⊕B0
其是一个3位的LFSR,其对应的多项式为
P ( X ) = 1 + X + X 3 P(X) = 1+X+X^3 P(X)=1+X+X3
因此执行除法运算有:
1 / ( 1 + X + X 3 ) = 1 + X + X 2 + X 4 + X 7 + X 8 + . . . 1/(1+X+X^3)=1+X+X^2+X^4+X^7+X^8+... 1/(1+X+X3)=1+X+X2+X4+X7+X8+...
代表的结果是111010011…,因此上述3位的LFSR产生的序列为1110100,周期为7,是3位LFSR的最大周期。注意,这里的除法并不是通常意义的除法,这里多项式系数的减法是模2运算,因此减法的结果和加法的效果相同。其执行过程如下

可以证明,当且仅当特征多项式是本原多项式时,那么其所产生的的序列是m序列(最大长度序列),比如上述的特征多项式 P ( X ) = 1 + X + X 3 P(X) = 1+X+X^3 P(X)=1+X+X3就是一个本原多项式。
本原多项式
本原多项式是近世代数中的一个概念,首一多项式 f ( x ) f(x) f(x)是有限域 G F ( p ) GF(p) GF(p)上的n次本原多项式,当且仅当 f ( x ) = 0 f(x)=0 f(x)=0的根是有限域 G F ( p n ) GF(p^n) GF(pn)上非零元素的生成元。域F中的生成元 g g g是指 g g g的前 q − 1 q-1 q−1个幂构成了域F中的所有元素,即域F中的元素是 0 , g 0 , g 1 , . . . , g q − 2 0,g^0,g^1,...,g^{q-2} 0,g0,g1,...,gq−2。
尽管LFSR有如上的许多优点,但是单个LFSR并不适合作为流密码来使用,主要由以下三个原因:
- 流密码由明文和LFSR产生的密钥流逐位异或生成密文,那么LFSR中保持的初始值包含了密钥的一部分
- 若LFSR中保持的初始值未知,但反馈函数已知,且敌手可以确定LFSR序列中的连续n位,那么敌手可以确定整个LFSR序列
- 若LFSR中保持的初始值和反馈函数均,但敌手可以确定LFSR序列中的连续2n位,那么敌手可以确定整个LFSR序列
上述原因中的第二点和第三点是因为反馈函数是线性的,因此通过列方程的形式便可唯一确定反馈函数,因此单个LFSR并不安全。常用情况下,有以下两种方法可以解决上述问题:
- 使用多个LFSR,它们的长度不同,并以某种方式组合在一起
- 使用非线性反馈移位寄存器
2.3.2 非线性反馈移位寄存器
非线性反馈移位寄存器中的反馈函数并不具备前述的 f ( x + y ) = f ( x ) + f ( y ) f(x+y)=f(x)+f(y) f(x+y)=f(x)+f(y)且 a f ( x ) = f ( a x ) af(x)=f(ax) af(x)=f(ax)的性质,它们常常有更为复杂的表示,比如:
f ( x ) = B 4 ⊕ B 3 B 2 f(x)=B_4\oplus B_3B_2 f(x)=B4⊕B3B2
即 B 5 = B 4 ⊕ B 3 B 2 B_5 = B_4\oplus B_3B_2 B5=B4⊕B3B2,其对于的特征多项式为:
P ( X ) = 1 + X + X 2 X 4 P(X)=1+X+X^2X^4 P(X)=1+X+X2X4
显然这样的表达式能够产生的序列是不易分析的,因此没有理论来证明其周期性的情况,因此NFSR并不单独使用。在实际中,往往结合LFSR和NFSR来产生周期大、安全性高的流密码。