高级加密标准AES

1. 有限域基础
2. AES设计
3. AES分析

作为DES密码算法的替代，美国国家标准和技术协会（NIST）于2001年发布了高级加密标准AES（Advanced Encryption Standard），其在比利时计算机科学家Vincent Rijmen和Joan Daemen开发的Rijndael算法基础上进行加工而来。和DES类似，AES是一个对称分组密码，使用了复杂的代替和置换技术来增加扩散和混淆，下面就详细讲述一下AES的基本思想和具体实现。

更新历史：

2021年08月08日完成初稿

1. 有限域基础

在有限域一文中介绍了关于群、环和域的基本知识，并在最后讨论了有限域 $GF(2^n)$ ，下面简单回顾一下有限域的知识并介绍本文涉及的有限域算术。

域是一种具有两个二元运算的代数系统，通常用加法和乘法表示两种运算，记作 $\times>$ 。集合F中的元素个数称为域F的阶，若运算个数是有限的，则称该域为有限域。可以证明，有限域只能被表示为 $GF(p^n)$ （p是素数，n是正整数），其上的集合通常为剩余类集合 $Z_{p^n}$ ，在AES中使用了两种有限域 $G F (2)$ 和 $GF(2^n)$ 。

AES首先使用了定义在 $G F (2)$ 的多项式 $f (x)$ ，即

$f(x)=a_{n-1}x^{n-1}+a_{n-2}x^{n-1}+...+a_1x+a_0\qquad a_i\in Z_2=\{0,1\}$

其中 $f (x)$ 最高次幂称为 $f (x)$ 的次数，之后定义了集合S为所有多项式 $f (x)$ 的集合：

$S=\{f(x)|f(x)=a_{n-1}x^{n-1}+a_{n-2}x^{n-1}+...+a_1x+a_0\qquad a_i\in Z_2=\{0,1\}\}$

显然，集合S有 $2^n$ 个元素，基于集合S定义了两种运算：模 $m (x)$ 加法和模 $m (x)$ 乘法，其中 $m (x)$ 是定义在 $G F (2)$ 上的n次不可约多项式（即不能在 $G F (2)$ 上进行因式分解），对于多项式 $f (x)$ 和 $g (x)$ 的加法和乘法为

扫描二维码关注公众号，回复： 14695814 查看本文章

$f(x)=a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+...+a_1x+a_0\qquad a_i\in Z_2=\{0,1\}\\ g(x)=b_{n-1}x^{n-1}+b_{n-2}x^{n-2}+...+b_1x+b_0\qquad b_i\in Z_2=\{0,1\}\\ f(x)+g(x)=(\sum_{i=0}^{n-1}(a_i+b_i)x^i)\;mod\;m(x)\qquad a_i+b_i=(a_i+b_i)\;mod\;2\\ f(x)\times g(x)=(\sum_{k=0}^{2n-2}(\sum_{i+j=k}a_ib_jx^{k}))\;mod\;m(x)\qquad \sum_{i+j=k}a_ib_jx^{k}=(a_0b_{k}+...+a_kb_0)\;mod\;2$

即多项式 $f (x)$ 和 $g (x)$ 的加法和乘法，可以先按照高中数学的多项式相加和相乘之后，对所有系数模2，最后对整个多项式模 $m (x)$ 。

AES中使用了 $GF(2^8)$ ，并利用了8次不可约多项式 $m(x)=x^8+x^4+x^3+x+1$ ，并将二进制串 $A=(a_7a_6...a_0)$ 和 $B=(b_7b_6...b_0)$ 表示成定义在 $G F (2)$ 的多项式，之后进行加法和乘法操作：

$A=(a_7a_6...a_0)\rightarrow f(x)=a_{7}x^{7}+a_{6}x^{6}+...+a_1x+a_0\\ B=(b_7b_6...b_0)\rightarrow g(x)=b_{7}x^{7}+b_{6}x^{6}+...+b_1x+b_0\\ f(x)+g(x)=(\sum_{i=0}^{7}(a_i+b_i)x^i)\;mod\;m(x)\rightarrow A+B=((a_7+b_7)\;mod\;2,...,(a_0+b_0)\;mod\;2)=A\oplus B$

因此多项式加法变成了对应二进制串的按位异或运算，例如：

$f(x)+g(x)=(x^6+x^4+x^2+x+1) + (x^7+x+1)=x^7+x^6+x^4+x^2\\ \qquad\qquad\qquad\quad(01010111) \oplus(10000011)\;=11010100$

不过对于乘法而言，就没有这么好的性质了，不过仍有一些简便的方法来实现运算。可以发现对于 $m(x)=x^8+x^4+x^3+x+1$ ，有：

$x^8\;mod\;m(x)=m(x)-x^8=x^4+x^3+x+1$

考虑 $GF(2^8)$ 上的多项式

$f(x)=b_7x^7+b_6x^6+b_5x^5+b_4x^4+b_3x^3+b_2x^2+b_1x+b_0$

那么对于多项式模运算 $x\times f(x)$ 有：

若 $b_7=0$ ，则 $x\times f(x)\;mod\;m(x)=b_6x^7+b_5x^6+b_4x^5+b_3x^4+b_2x^3+b_1x^2+b_0x$
若 $b_7\ne0$ （即 $b_7=1$ ）则

$x\times f(x)\;mod\;m(x)=(x^8\;mod\;m(x))+(b_6x^7+b_5x^6+b_4x^5+b_3x^4+b_2x^3+b_1x^2+b_0x)\\ \qquad\qquad\qquad\qquad\quad\;\;=(x^4+x^3+x+1)+(b_6x^7+b_5x^6+b_4x^5+b_3x^4+b_2x^3+b_1x^2+b_0x)$

用二进制表示即为

$x\times f\left( x \right) =\begin{cases} b_6b_5b_4b_3b_2b_1b_00,\qquad\qquad\qquad\;\;\; b_7=0\\ b_6b_5b_4b_3b_2b_1b_00\oplus 00011011\qquad b_7=1\\ \end{cases}$

而乘以 $x$ 的更高次幂可以反复进行上面的计算，比如计算 $f(x)=x^6+x^4+x^2+x+1,\;g(x)=x^7+x+1$ 的乘法，则有：其中

$01010111\times 00000010=10101110\qquad\qquad\qquad\qquad\qquad\;\;\\ 01010111\times 00000100=01011110\oplus 00011011=01000111\\ 01010111\times 00001000=10001110\qquad\qquad\qquad\qquad\qquad\;\;\\ 01010111\times 00010000=00011100\oplus 00011011=00000111\\ 01010111\times 01000000=00001110\qquad\qquad\qquad\qquad\qquad\;\;\\ 01010111\times 01000000=00011100\qquad\qquad\qquad\qquad\qquad\;\;\\ 01010111\times 10000000=00111000\qquad\qquad\qquad\qquad\qquad\;\;\\ \;\\ f(x)\times g(x)=f(x)\times x^7 + f(x)\times x+f(x)\qquad\qquad\qquad\qquad\\ =01010111\times 10000011\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\\ =01010111\times(10000000\oplus 00000010 \oplus 00000001)\qquad\quad\quad\;\;\;\\ =00111000\oplus 10101110\oplus 01010111=11000001\qquad\qquad\quad\;\;\\$

故 $f(x)\times g(x)=x^7+x^6+1$

以上便是AES中使用到的有限域的基本知识和算术，下面具体讲述AES的设计和分析。

2. AES设计

2.1 AES基本结构

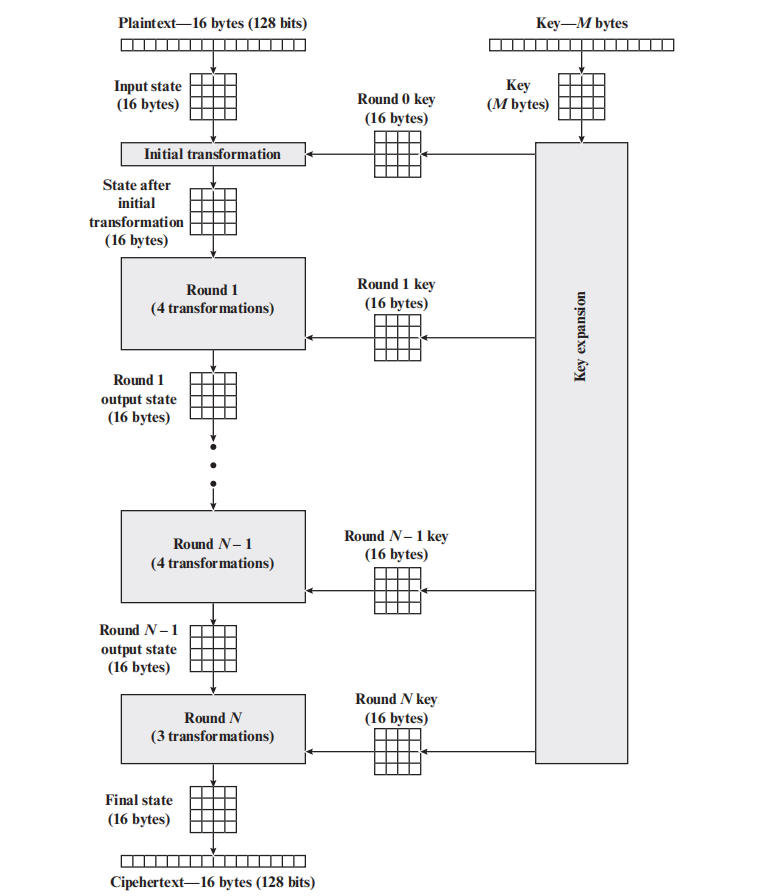
AES是一种对称分组密码，其明文分组和密文分组为128位（16字节），密钥长度通常为128位（也可以是192位、256位等），并根据密钥长度进行N轮运算，通常密钥为16字节时N=10，24字节时N=12，32字节时N=14，下面是AES是一般加密过程：

其中，128比特的明文以4阶矩阵表示，经过N轮运算加密成128比特的密文，N轮运算中每轮经过4种变换（最后一轮是3种变换）：字节代替、行移位、列混淆和轮密钥加。在加密过程中M比特的密钥也会以矩阵形式表示，并扩展成每一轮的密钥（每一轮密钥均不同，由上一密钥变换而来），下面以M=128，N=10为例介绍AES是具体加密和解密过程，在加密和解密过程中有两部分十分重要：

明文变换：字节代替、行移位、列混淆和轮密钥加的具体变换过程
密钥扩展：密钥的扩展运算并形成子密钥

图2.1 AES一般加密过程

2.2 AES具体设计

下面将介绍使用16字节密钥，10轮变换的AES具体的结构和变换函数，初看起来，AES有很多变换，而且密钥扩展过程十分地复杂，不过下面会提醒读者如何更好地阅读本节。

2.2.1 AES具体结构

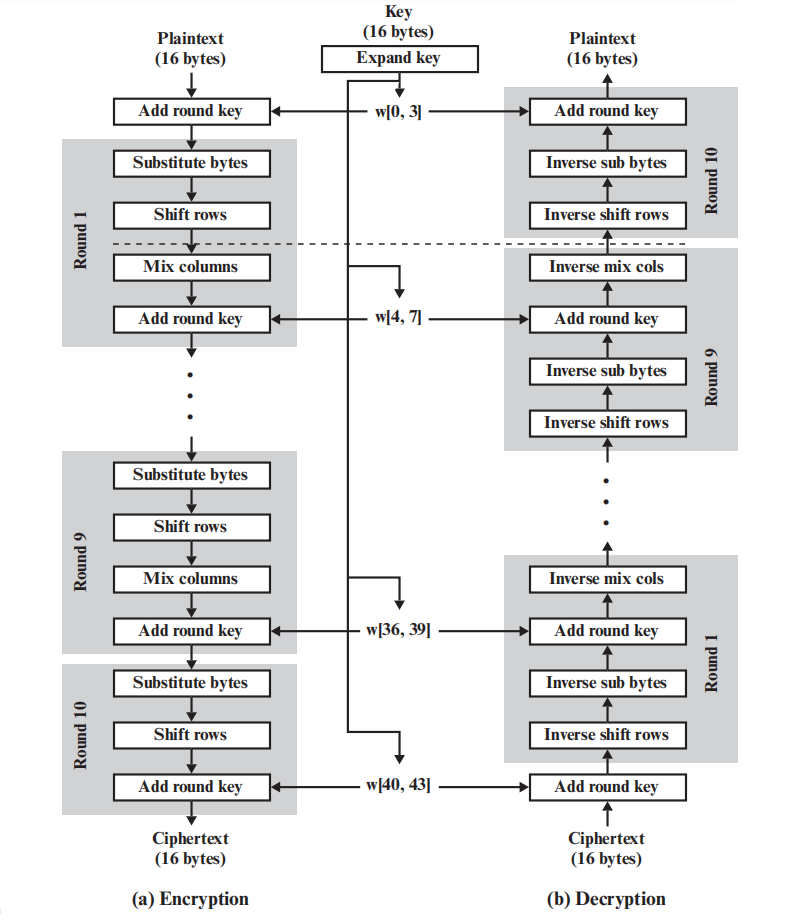
使用16字节密钥的AES的加密过程和解密过程如图2.2所示，可以看到AES虽然和DES一样使用了大量的代替和置换运算，但并不像DES一样使用Feistel结构，因为AES明文并没有分成左右部分而是以矩阵形式表示。

对于加密和解密过程中的明文和密文变换，明文首先进行轮密钥加运算，之后经过10轮的代替和置换变换：

字节代替（Substitute bytes）：用一个S盒完成分组的字节到字节的代替
行移位（Shift rows）：一个简单的置换
列混淆（Mix columns）：利用有限域 $GF(2^8)$ 上的算术特性的一个代替（最后一轮，即第10轮没有列混淆）
轮密钥加（Add round key）：当前分组和拓展密钥的一部分进行按位异或运算

上述四个阶段都是可逆的，也正因为如此在最后一轮（第10轮）没有列混淆运算。

另外值得注意的是轮密钥的产生，初始时16字节的密钥经过扩展生成了176字节的密钥并分成11组w[0,3]，w[4,7]，…，w[40,43]。这些密钥也被用于加密和解密运算中的轮密钥加，在后面的例子中可以发现每一轮的轮密钥都是不一样的。

图2.2 16字节密钥的AES的加密和解密过程

2.2.2 AES变换函数

下面就可以讨论一下具体的AES变换的过程，这里暂时不讲述密钥的扩展过程，而假设每一轮的密钥都可以直接使用，下一小节将会讨论这一点。以明文plaintext=0xEA835CF00445332D655D98AD8596B0C5（十六进制）。

按照之前的讲述16字节的明文将组织成4阶方阵，下面是AES加密过程中的数据组织形式：

图2.3 AES数据组织形式

因此在进行变换之前，明文被组织成：

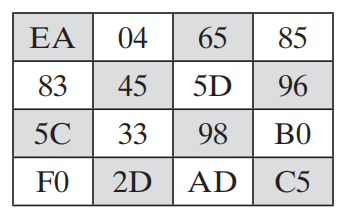
下面正式介绍具体的四种变换，在介绍过程中，始终关注以下3点：

正向变换如何进行的？
逆向变换如何进行的？
该变换有什么作用？

2.2.2.1 字节代替变换

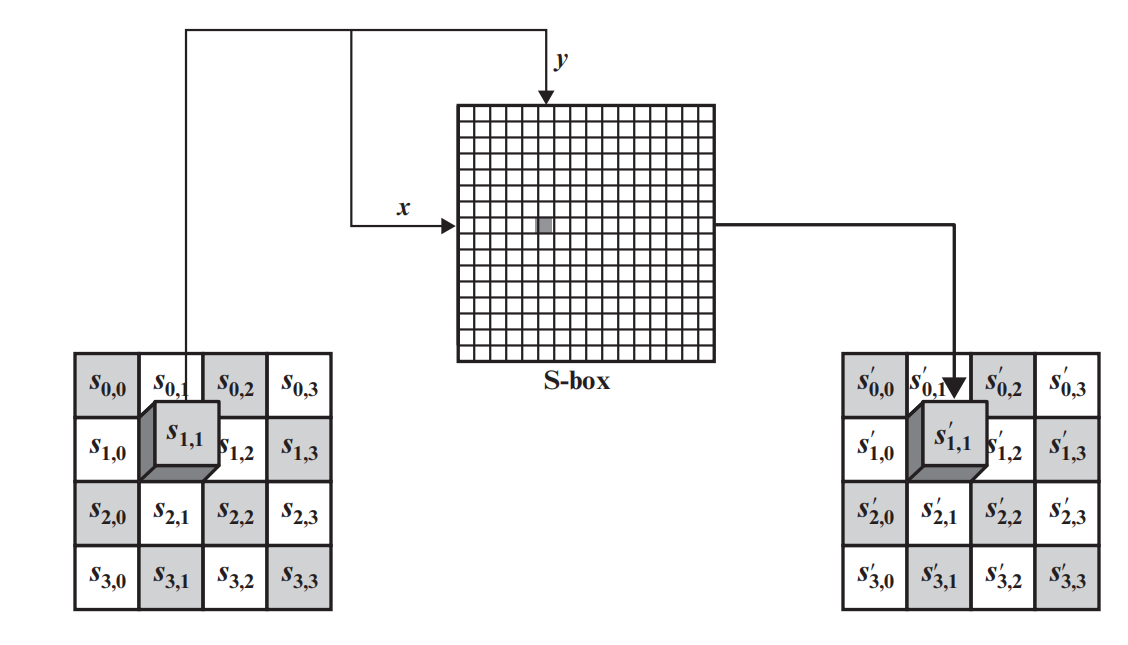
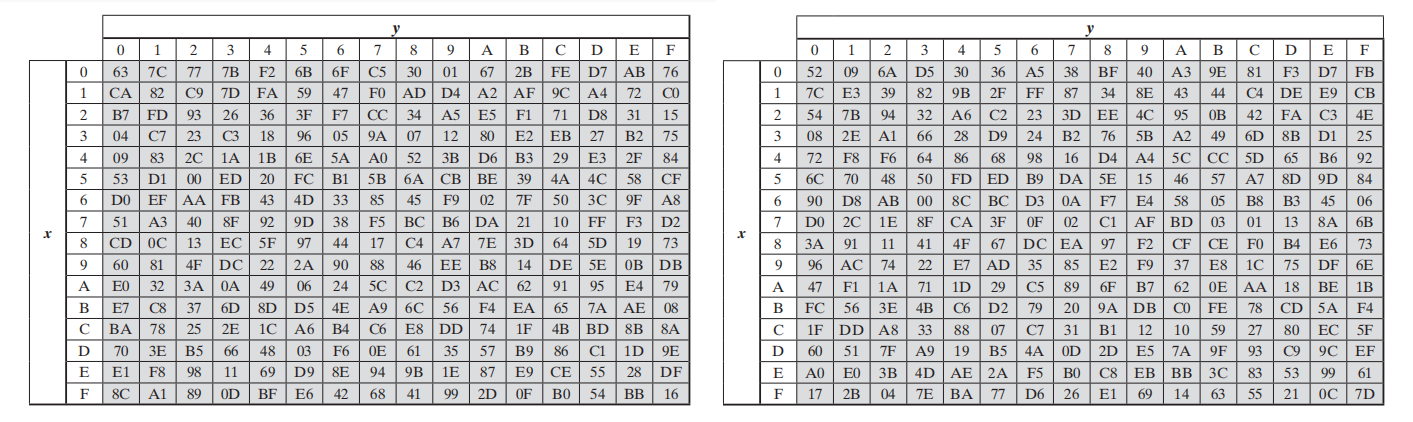
字节代替变换有正向变换和逆向变换两种，正向字节代替变换是一个查表操作，其示意图如图2.4所示。其中需要对S盒进行查表，S盒和逆S盒如图2.5所示。

其中每一个字节，前4比特是行号，后4比特是列号，比如S1,1对应45，因此行号是4（即x=4），列号是5（即y=5），查S盒可知6E，一次类推可完成字节代替变换，最终可以得到：

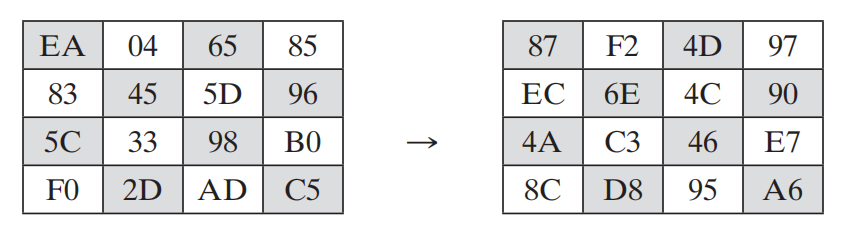
在逆向字节代替中，同样可以查找逆S盒来实现解密的过程。

值得注意的是，AES中的S盒是经过精心构造的，在S盒生成过程中有一个步骤为：将S盒中的每个字节映射为它在有限域 $GF(2^8)$ 中的乘法逆元，这一步骤使得字节代替变换具有了非线性的特点，因此可以达到很好的扩散效果。

图2.4 正向字节代替变换

图2.5 S盒（左）和逆S盒（右）

2.2.2.2 行移位变换

同样地，行移位变换也有正向和逆向变换，对于正向变换有：第一行保持不变，第二行循环左移1字节，第三行循环左移2字节，第三行循环左移3字节，如图2.6所示。

图2.6 正向行移位变换

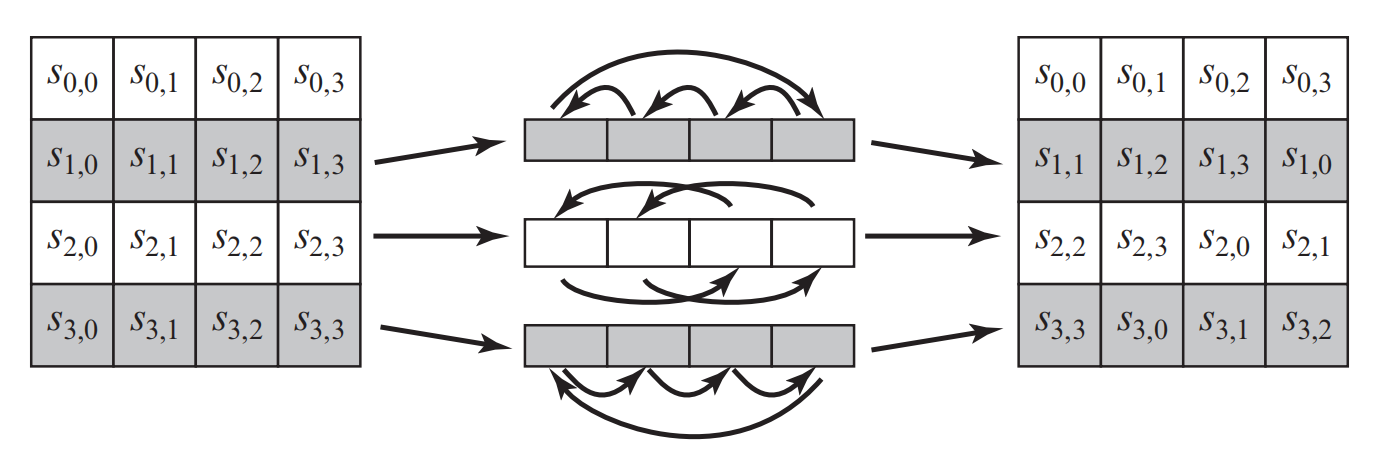
因此对于2.2.2.1节得到的矩阵经过变换有：

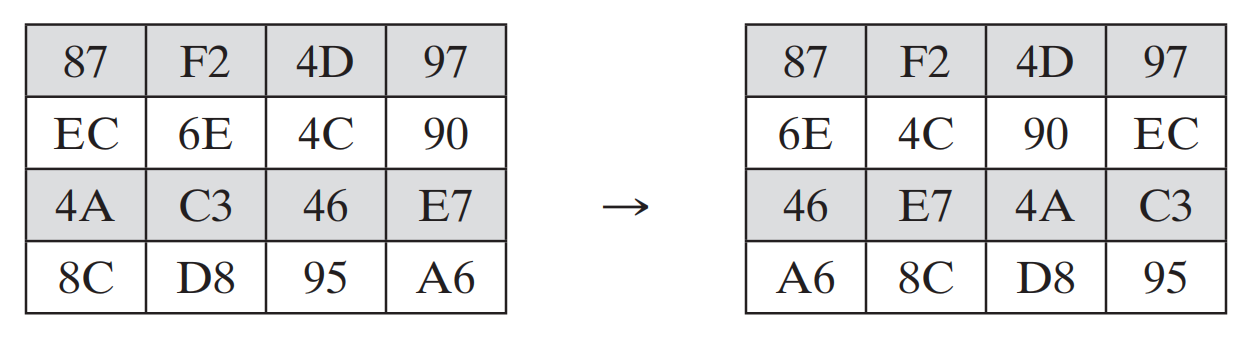
对于逆向变换，其只要对后三行进行反向得到移位运算即可，即第一行保持不变，第二行循环右移1字节，第三行循环右移2字节，第三行循环右移3字节。

行移位是十分简单的变换，只通过移位运算即可实现，即使看起来很简单，但其作用也是十分明显的，对比经过行移位变换的矩阵可以发现：原来在同一列的元素被置换到不同列了。比如变换前87 EC 4A 8C在同一列，而变换后87在第1列，EC在第4列，4A在第3列，8C在第2列。

2.2.2.3 列混淆变换

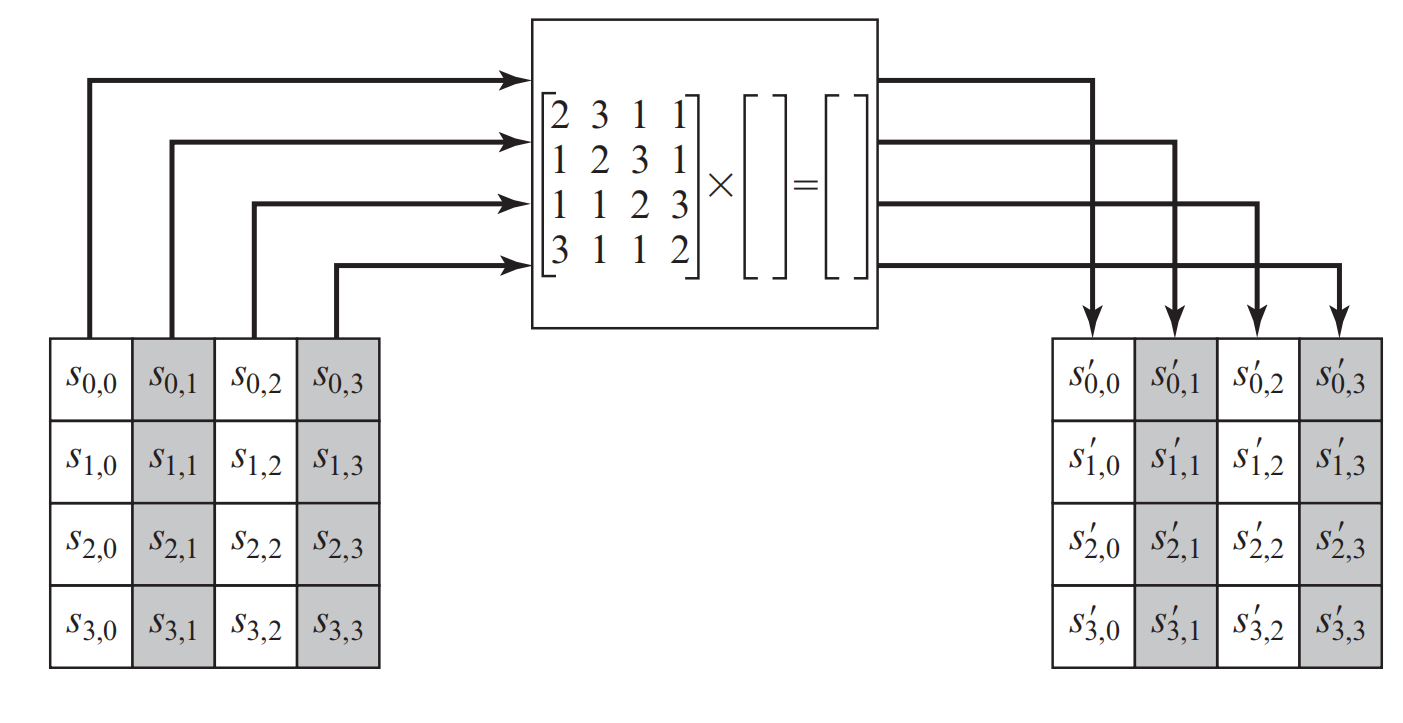
对于列混淆变换来说，同样有正向和逆向变换，不过在这里正向变换比逆向变换简单很多，这也是为了让攻击者难以解密。对于正向列混淆变换而言，其对每列都进行独立的计算，每列中的每个字节都被映射为一个新值，图2.7就是变换的具体过程。

该变换可以由下式描述：

$\left[ \begin{matrix} 02& 03& 01& 01\\ 01& 02& 03& 01\\ 01& 01& 02& 03\\ 03& 01& 01& 02\\ \end{matrix} \right] \left[ \begin{matrix} s_{0,0}& s_{0,1}& s_{0,2}& s_{0,3}\\ s_{1,0}& s_{1,1}& s_{1,2}& s_{1,3}\\ s_{2,0}& s_{2,1}& s_{2,2}& s_{2,3}\\ s_{3,0}& s_{3,1}& s_{3,2}& s_{3,3}\\ \end{matrix} \right] =\left[ \begin{matrix} s_{0,0}^{'}& s_{0,1}^{'}& s_{0,2}^{'}& s_{0,3}^{'}\\ s_{1,0}^{'}& s_{1,1}^{'}& s_{1,2}^{'}& s_{1,3}^{'}\\ s_{2,0}^{'}& s_{2,1}^{'}& s_{2,2}^{'}& s_{2,3}^{'}\\ s_{3,0}^{'}& s_{3,1}^{'}& s_{3,2}^{'}& s_{3,3}^{'}\\ \end{matrix} \right]$

即有下式，其中的乘法需要利用有限域 $GF(2^8)$ 上面的乘法来完成：

$s_{0,j}^{'}=(02\cdot s_{0,j})\oplus (03\cdot s_{1,j})\oplus (01\cdot s_{2,j})\oplus (01\cdot s_{3,j})\\ s_{1,j}^{'}=(01\cdot s_{0,j})\oplus (02\cdot s_{1,j})\oplus (03\cdot s_{2,j})\oplus (01\cdot s_{3,j})\\ s_{2,j}^{'}=(01\cdot s_{0,j})\oplus (01\cdot s_{1,j})\oplus (02\cdot s_{2,j})\oplus (03\cdot s_{3,j})\\ s_{3,j}^{'}=(01\cdot s_{0,j})\oplus (01\cdot s_{1,j})\oplus (01\cdot s_{2,j})\oplus (02\cdot s_{3,j})$

图2.7 正向列混淆变换

下面就有2.2.2.2节的例子来说明一下具体的计算过程：

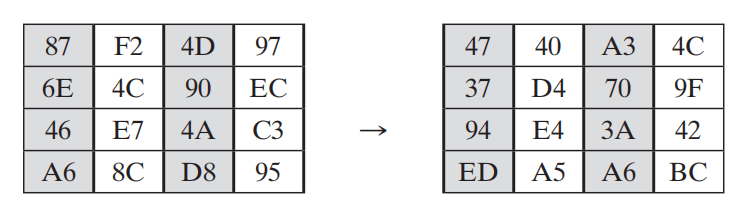
下面证明所得结果的第一列：
$02\cdot 87\oplus 03\cdot 6E\oplus 01\cdot 46\oplus 01\cdot A6=47\\ 01\cdot 87\oplus 02\cdot 6E\oplus 03\cdot 46\oplus 01\cdot A6=37\\ 01\cdot 87\oplus 01\cdot 6E\oplus 02\cdot 46\oplus 03\cdot A6=94\\ 03\cdot 87\oplus 01\cdot 6E\oplus 01\cdot 46\oplus 02\cdot A6=ED$

根据文章最开头介绍的有限域算术（在那里乘法是用 $\times$ 而不是 $\cdot$ ）：

$x\cdot f\left( x \right) =00000010\cdot b_7b_6b_5b_4b_3b_2b_1b_0=\begin{cases} b_6b_5b_4b_3b_2b_1b_00,\qquad\qquad\qquad\;\;\; b_7=0\\ b_6b_5b_4b_3b_2b_1b_00\oplus 00011011\qquad b_7=1\\ \end{cases}$

计算 $02\cdot 87\oplus 03\cdot 6E\oplus 01\cdot 46\oplus 01\cdot A6$ 有：

$02\cdot 87=10000111\oplus 00000010=00001110\oplus 00011011=00010101\\ 03\cdot 6E=01101110\oplus(00000010+00000001)=11011100\oplus01101110=10110010\\ 01\cdot 46=01000110\\ 01\cdot A6=10100110\\ 02\cdot 87\oplus 03\cdot 6E\oplus 01\cdot 46\oplus 01\cdot A6=00010101\oplus10110010\oplus 01000110\oplus10100110=01000111=47$

其他等式可以按照类似推算得出。对于逆向列混淆变换，可以证明其可由下面的矩阵乘法来表示：

$\left[ \begin{matrix} 0E& 0B& 0D& 09\\ 09& 0E& 0B& 0D\\ 0D& 09& 0E& 0B\\ 0B& 0D& 09& 0E\\ \end{matrix} \right] \left[ \begin{matrix} s_{0,0}& s_{0,1}& s_{0,2}& s_{0,3}\\ s_{1,0}& s_{1,1}& s_{1,2}& s_{1,3}\\ s_{2,0}& s_{2,1}& s_{2,2}& s_{2,3}\\ s_{3,0}& s_{3,1}& s_{3,2}& s_{3,3}\\ \end{matrix} \right] =\left[ \begin{matrix} s_{0,0}^{'}& s_{0,1}^{'}& s_{0,2}^{'}& s_{0,3}^{'}\\ s_{1,0}^{'}& s_{1,1}^{'}& s_{1,2}^{'}& s_{1,3}^{'}\\ s_{2,0}^{'}& s_{2,1}^{'}& s_{2,2}^{'}& s_{2,3}^{'}\\ s_{3,0}^{'}& s_{3,1}^{'}& s_{3,2}^{'}& s_{3,3}^{'}\\ \end{matrix} \right]$

因为可以验算下式是成立的：

$\left[ \begin{matrix} 0E& 0B& 0D& 09\\ 09& 0E& 0B& 0D\\ 0D& 09& 0E& 0B\\ 0B& 0D& 09& 0E\\ \end{matrix} \right] \left[ \begin{matrix} 02& 03& 01& 01\\ 01& 02& 03& 01\\ 01& 01& 02& 03\\ 03& 01& 01& 02\\ \end{matrix} \right] =\left[ \begin{matrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ \end{matrix} \right]$

值得注意的是，正向变换矩阵中的系数为03、02、01、01，因此计算时最多涉及1次移位和1次异或运算，而逆向变换矩阵中的系数都时0E、0D、0B、09，因此计算都比较复杂，这也导致加密比解密快。有时，因为加密比解密重要（比如有些应用中只使用加密过程），所以这样的设计是合理的。

列混淆变换中，通过矩阵相乘的运算使得明文中的字节具有很好的混淆效果，而且经过几轮变换之后，列混淆变换和行移位变换使得所有输出位均与所有输入位相关。

2.2.2.4 轮密钥加

轮密钥加变换中，其实就是明文或者密文与轮密钥的按位异或，由于是按位异或，因此可以直接在矩阵上进行运算，如图2.8所示：

图2.8 正向轮密钥加

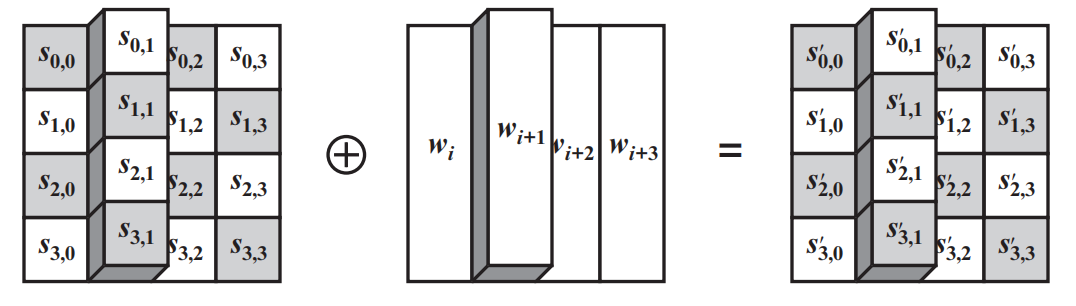
针对上节的例子，假设该轮的轮密钥为K=0xAC7766F319FADC2128D12941575C06A，因此可以进行下面的运算：

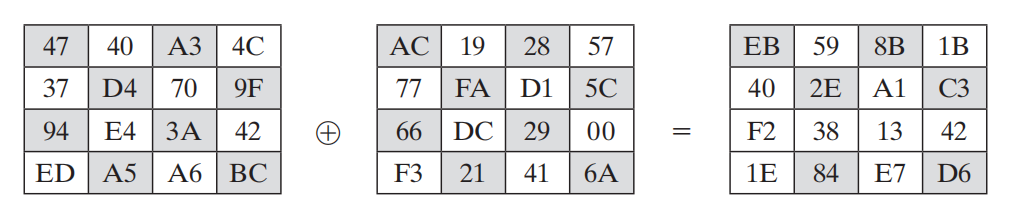
其中轮密钥的组织形式和明文组织形式是一致的。

对于逆向轮密钥加，其过程和正向过程也是一样的，因为 $P\oplus K\oplus K=P$ 。

理解轮密钥加变换是简单的，但是轮密钥加最关键的是每一轮的轮密钥都是不一样的，而且轮密钥和明文是按位异或，这样可以作用于所有位。结合上面几个变换，其实会发现整个过程已经十分复杂了，加上密钥扩展过程也是十分复杂的，这样的复杂的变换才保证了算法的安全性。

2.2.3 AES密钥扩展

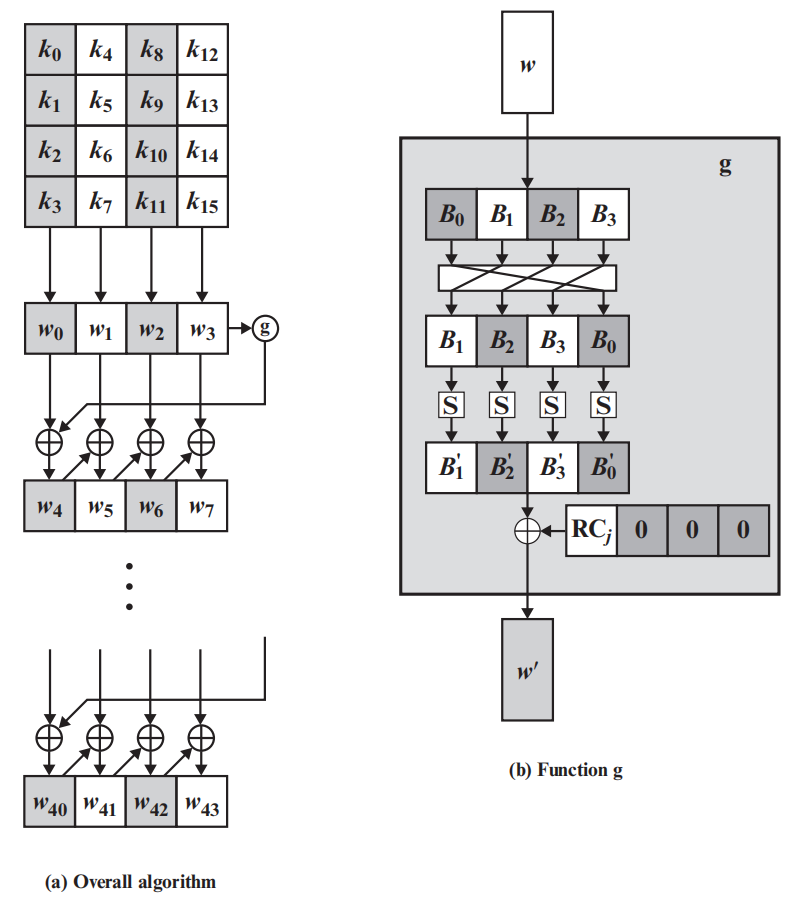
在上面的例子中，初始密钥只有16字节，但最终可以产生176字节从而运用到初始轮密钥加和10轮变换中，下面就介绍如何实现这样的过程，图2.9描述了密钥扩展的主要流程。

首先，16字节的密钥被组织成图中的4阶矩阵形式，然后有：

$w_0=k_0k_1k_2k_3,\quad w_1=k_4k_5k_6k_7,\quad w_2=k_8k_9k_{10}k_{11},\quad w_3=k_{12}k_{13}k_{14}k_{15}$

然后密钥扩展

$w_4=w_0\oplus g(w_3),\quad w_5=w_1\oplus w_4,\quad w_6=w_2\oplus w_5,\quad w_7=w_3\oplus w_6$

其中g是一个更复杂的函数，经过不断的密钥扩展便可以产生所有轮密钥。下面介绍一下函数g，函数g以4字节为单位作为输入，然后经过下面的变换：以4字节 $w=B_0B_1B_2B_3$ 为例

循环移位：以1字节为单位进行循环左移： $B_0B_1B_2B_3\rightarrow B_1B_2B_3B_0$
S盒变换：对于每个字节都进行S盒进行字节代替（高4位作为行，低4位作为列），S盒见图2.5： $B_1B_2B_3B_0\rightarrow B_{1}^{'}B_{2}^{'}B_{3}^{'}B_{0}^{'}$

异或运算：将S盒变换的结果 $B_{1}^{'}B_{2}^{'}B_{3}^{'}B_{0}^{'}$ 与字节 $0xRC_j000000$ 进行异或，其中 $RC_j$ 被定义为如下值（RC[j]即 $RC_j$ ）：

j	1	2	3	4	5	6	7	8	9	10
RC[j]	01	02	04	08	10	20	40	80	1B	36

图2.9 AES密钥扩展

假设第8轮的轮密钥为K=0xEAD27321B58DBAD2312BF5607F8D292F，那么有：

$w_{32}=0xEAD27321,\quad w_{33}=0xB58DBAD2,\quad w_{34}=0x312BF560,\quad w_{35}=0x7F8D292F$

则有下一轮密钥为：

$w_{36}=w_{32}\oplus g(w_{35}),\quad w_{37}=w_{33}\oplus w_{36},\quad w_{38}=w_{34}\oplus w_{37},\quad w_{39}=w_{35}\oplus w_{38}$

其中 $g(w_{35})$ 有： $w=B_0B_1B_2B_3=0x7F8D292F$ ，故有：

循环移位： $w_1=B_1B_2B_3B_0=0x8D292F7F$
S盒变换： $w_2=B_{1}^{'}B_{2}^{'}B_{3}^{'}B_{0}^{'}=0x5DA515D2$
异或运算：RC[9]=1B，故 $w'=B_{1}^{'}B_{2}^{'}B_{3}^{'}B_{0}^{'}\oplus0xRC_j000000=0x5DA515D2\oplus(0x1B000000)=0x46A515D2$

因此 $g(w_{35})=0x46A515D2$ ，故有：

$w_{36}=w_{32}\oplus g(w_{35})=0xEAD27321\oplus 0x46A515D2=0xAC7766F3\\ w_{37}=w_{33}\oplus w_{36}=0xB58DBAD2\oplus 0xAC7766F3=0x19FADC21\\ w_{38}=w_{34}\oplus w_{37}=0x312BF560\oplus 0x19FADC21=0x28D12941\\ w_{39}=w_{35}\oplus w_{38}=0x7F8D292F\oplus 0x28D12941=0x575C006E$

根据上面的叙述，可以用下列伪代码描述密钥扩展过程：

KeyExpansion(byte key[16], word w[44]){  // 输入16字节密钥key[16]，输出44字w[44]（1字等于4字节）
    word temp ;
    for(i = 0; i < 4; i++){
        w[i] = key[4*i] + key[4*i+1] + key[4*i+2] + key[4*i+3] ;
    }
    for(i = 0; i < 44; i++){
        temp = w[i-1] ;
        if(i mod 4 == 0){
            temp = SubWord(RotWord(temp)) + RC[i/4] ;  // SubWord()为S盒字节替代，RotWord()为循环移位
        }
        w[i]=w[i-4] + temp                             // 第9行和第11行的加法为按位异或运算
    }
}

对于AES密钥扩展而言，通过上面的描述可以发现其实密钥扩展十分复杂，每一轮的轮密钥都取决于上一轮所有轮密钥，而且由于引入常量 $RC_j$ 使得密钥具有很好的非对称性，从而很难由部分轮密钥推算出所有轮密钥。

3. AES分析

AES中最重要的有两部分：

AES变换函数：字节代替、行移位、列混淆和轮密钥加
AES轮密钥扩展

这两部分使得加密过程足够复杂，而且具有非线性的特点，使得AES攻击变得十分困难。另外，和DES一样，AES具有很强的雪崩效应：

雪崩效应：明文或者密钥的一位变化就可以引起密文的很多位发生变化

根据测试，改变明文或者密钥中的一位，最终大概密文改变的位数为 $64$ 比特左右，大概是密文位数 $128$ 比特的一半，而且经过三四轮函数加密后就达到这样的效果，这是十分好的性质，因为如果改变明文或者密钥中的一位而密文也不会改变太多位，那么攻击者可以针对这一点进行攻击。

因此AES在一定程度上是比较安全的。

【密码学基础】06 高级加密标准AES