前言

系统由一辆具有动力的小车和安装在小车上的倒立摆组成，系统是不稳定，我们需要通过控制移动小车使得倒立摆保持平衡。

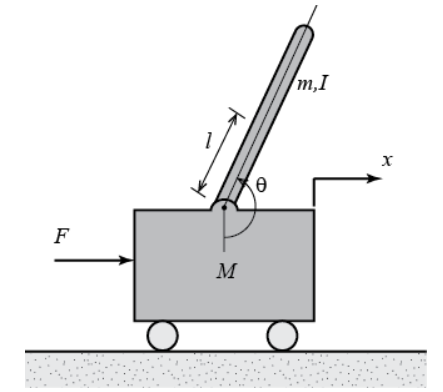
具体地，考虑二维情形如下图，$l$为摆长的一半，$m,I$分别为摆的质量和转动惯量，控制力为水平力$F$，输出为角度$\theta$以及小车的位置$x$。

力分析和系统方程

设两个物体在水平和竖直方向上的相互作用力分别为$N$和$P$。
将小车水平方向上的力相加，得到牛顿力学方程：
$$M\ddot{x}+b\dot{x}+N=F$$

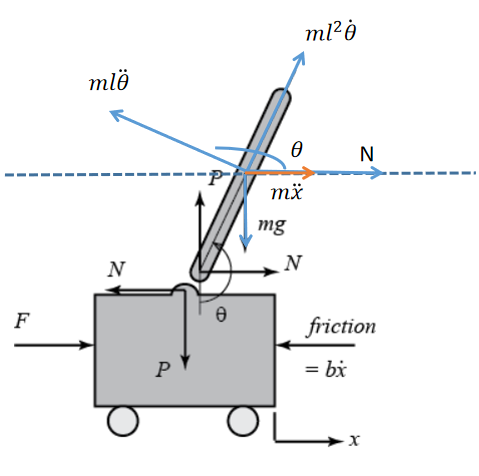
作用于摆上的力（惯性力）如上图所示，由于不存在沿摆径向的移动因而不存在科里奥利力，其中离心力为$m{l}^2\dot{\theta }$，转动加速度对应的惯性力为$ml\ddot{\theta }$，以及整个系统平动的加速度对应的惯性力为$m\ddot{x}$。

将倒立摆水平方向上的力相加，得到：
$$N=m\ddot{x}+ml\ddot{\theta }cos\theta -ml{\dot{\theta }}^{2}sin\theta$$
将$N$消去，得
$$M\ddot{x}+b\dot{x}+m\ddot{x}+ml\ddot{\theta }cos\theta -ml{\dot{\theta }}^{2}sin\theta =F$$
将垂直于摆的力相加，得
$$Psin\theta +Ncos\theta -mgsin\theta =ml\ddot{\theta }+m\ddot{x}cos\theta (a)$$
为了消去$P,N$两项，将围绕钟摆质心的力矩相加，得
$$-Plsin\theta -Nlcos\theta =I\ddot{\theta }(b)$$
$(a)\times l+(b)$得
$$(I+m{l}^2)\ddot{\theta }+mglsin\theta =-ml\ddot{x}cos\theta$$

线性化

系统的平衡点为$\theta =\pi$，并假设系统保持在这个平衡的小邻域内。设$\varphi$为摆对平衡位置的偏差，满足$\theta =\pi +\varphi$，若偏差十分小，使用以下近似：
$$\begin{gathered} cos\theta =cos(\pi +\varphi )\approx -1 \\ sin\theta =sin(\pi +\varphi )\approx -\varphi \\ {\dot{\theta }}^2={\dot{\varphi }}^2\approx 0 \end{gathered}$$

将上述近似公式应用至前面的非线性控制方程，得到两个线性化的方程，并使用$u$替代$F$得
$$\begin{gathered} (I+m{l}^2)\ddot{\varphi }-mgl\varphi =ml\ddot{x} \\ (M+m)\ddot{x}+b\dot{x}-ml\ddot{\varphi }=u \end{gathered}$$

传递函数

假设初始条件为0，对系统方程应用拉普拉斯变换：

$$\begin{gathered} (I+m{l}^2)\Phi (s)s^2-mgl\Phi (s)=mlX(s)s^2 \\ (M+m)X(s)s^2+bX(s)s-ml\Phi (s)s^2=U(s) \end{gathered}$$

通过四则运算可以得到$\frac{\Phi (s)}{U(s)},\frac{X(s)}{U(s)}$

reference

翻译自
Inverted Pendulum: System Modeling