目录
前言
对于大量的数据而言,链表的线性访问时间太慢,不宜使用。本章节将会介绍一种简单的数据结构:树(tree),其大部分操作的运行时间平均为O(logN)。在数据结构中树是非常有用的抽象概念,在本篇中我们将讨论一棵高阶搜索树——b树。前排提示:高阶搜索树的代码难度高出一个量级,建议先把逻辑理顺后再去看代码哦。
一、什么是B-tree
虽然迄今为止我们所看到的查找树都是二叉树,但是还有一种常用的查找树不是二叉结构的,这种树叫做B树(B-tree)。
那么问题来了,既然已经有了诸如AVL树的查找树,为什么还要存在B树呢?因为平衡树的数据放在内存当中,但在实际的项目中,数据量特别的大,要放在磁盘中,而面临大量数据时二叉树的高度大意味着与磁盘交互次数多,而每一次磁盘的I/O都是机械运动,读取速度相对于内存来说是很慢的,为了降低树的高度、减少磁盘I/O,B树就此诞生。
B树具有下列特性:
- 是一棵多路平衡树,一个节点有多个数据,通常要求空间大小和磁盘块的大小一致;
- 在逻辑上,所有的叶子都在同一层且不带信息;
- 对于节点规定了上界和下界,最常见的每个节点(根节点除外)包含【t-1,2t-1】个关键字(其中t是最小的度,t>=2),不是硬性规定,根据实际中的磁盘块来决定;
- 如果一个节点有x个关键字,就有x+1个孩子;
- 每一个节点的关键字按照升序排序,x和y之间孩子的范围就是(x, y)。
为了使大家在概念上更方便理解,正如先前在二叉排序树中做的那样,我们使实际的数据存储在叶子上,也可以存储在内部节点中。实际上B树有多种定义,这些定义在一些次要的细节上不同于我们定义的结构。如下所示就是一棵B树:

这里还要提一个概念,图中的B树是4阶B树的一个例子,它的更流行的称呼是2-3-4树,而3阶B树称作2-3树;我们将通过这棵2-3-4树来描述B树增删查改。
二、查找
B树的查找和二叉排序树的查找过程十分相似,唯一不同的是:二叉排序树的任意一个节点最多只能有两个孩子,而B树则最多可以有M+1个孩子(M为节点中关键字个数),但这并不影响我们用与二叉排序树相同的查找方法,只需要多一步在节点中的遍历(可以是顺序也可以是二分,方便就行),我在代码中对返回的结果做了封装,这样过程会更加规范,当然效果是一样的。
/*查找返回节点下标的函数 从1到keynum找key*/
int search(BTree p, KeyType key)
{
int i = 1;
while (i <= p->keynum && key > p->key[i])
{
i++;
}
return i;
}
/*返回封装的结果集的查找函数 不是真正进行查找步骤*/
void searchNode(BTree tree, KeyType key, Result& r)
{
int i;
int found = 0;//标记查找成功或者失败 成功是1 失败是0
//先定义指针指向根节点
BTree p = tree;
BTree q = NULL;//有时候需要指向双亲节点的指针
while (p != NULL)
{
i = search(p, key);
if (i <= p->keynum && key == p->key[i])
{
//不允许重复所以找到就是查找失败 说明这个数据已经存进去了
found = 1;
}
else
{
q = p;
p = p->ptr[i - 1];//指针下移
}
}
//如果查找到了
if (found == 1)
{
r.pt = p;
r.i = i;
r.tag = found;
}
//没有查找到
else
{
//没有找到就把父节点传回去 利于后续操作
r.pt = q;
r.i = i;
r.tag = found;
}
}
三、插入
B树的插入规则与二叉排序树的插入类似,即一个节点中的关键字总是有序的,并且总是要插入到实际的叶子节点;不同的是,为了满足B树的高度可控这一特性,需要时刻判断是否超过了规定的存储最大容量,如果达到容量上限就要进行分裂(split);

有如上一棵2-3树,当我们试图插入新关键字K时,发现K所属的节点已经满了,插入K将使得这个节点拥有四个关键字,这是不允许的,这时我们就要分裂,从中间对半分,得到两个新的节点;

但此时我们又发现,分裂出的新节点的父节点现在有了四个孩子,而它只有两个关键字,最多只能有三个孩子,这样又带来了一个新的问题,当然解决的办法也很简单,我们可以把中间值上移,是父节点的关键变成三个,这样父节点最大就能有四个孩子了。

分裂是维持B树性质的重要操作之一,一定要把逻辑理清楚!接下来我们对上文中的2-3-4树再过一遍完整的插入流程:
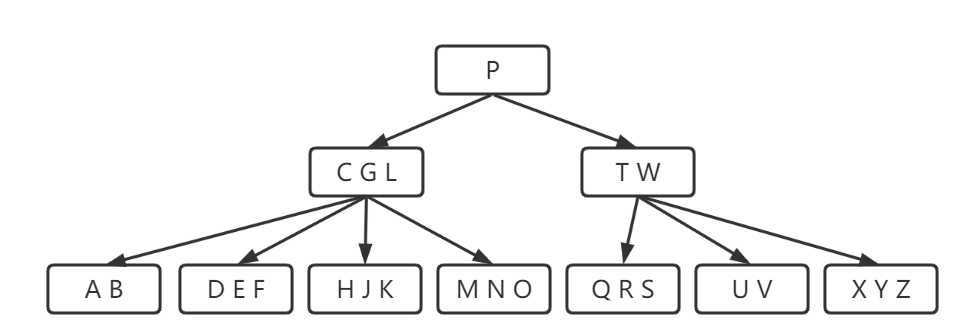
第一步:判断根节点是否初始化,如果没有,初始化root为根节点;
第二步:当我们插入节点i,与根节点p比较,小于就往左边插入;
第三步:发现p的左孩子节点已经满了,需要分裂;
第四步:继续比较,比L小,插L的左子树;
第五步:判断L的左子树是否满了,满了就分裂,没满就挨个比较找到正确的插入位置插入,结束。
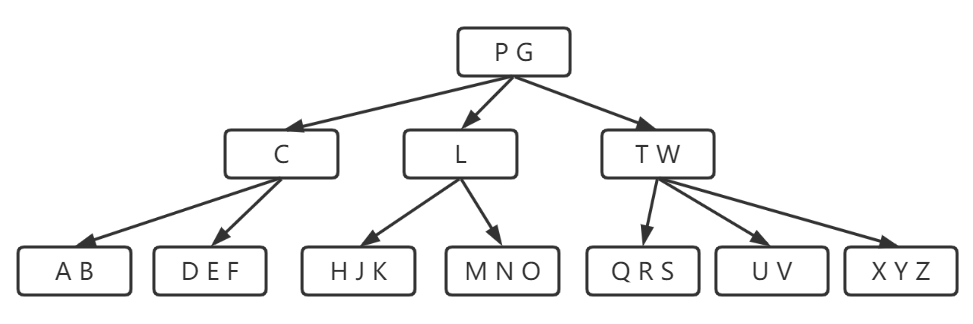
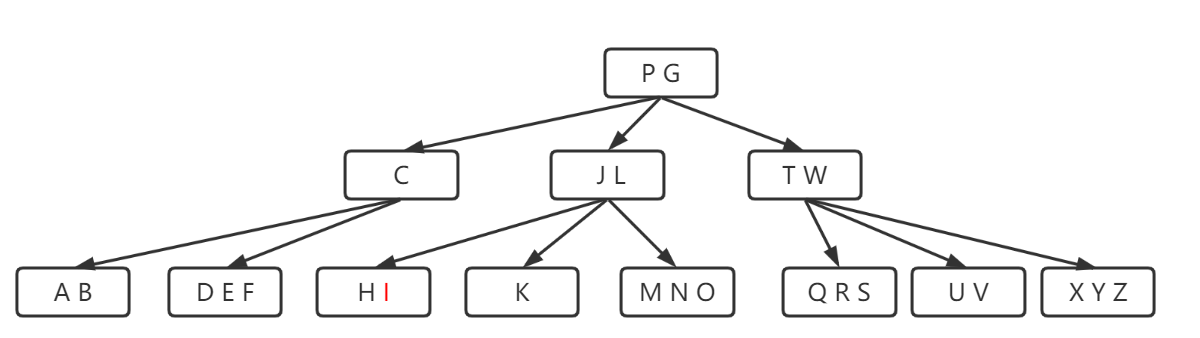
我们会发现在执行分裂操作时,永远都是从中间对半分、把中间值往上递,且这个步骤在插入的过程中会一直检测并进行,不需要像AVL树一般有一个回溯的过程,像这种平衡的机制我们称作自平衡,也可见B树是不存在不平衡的机会的;
而要简单的实现自平衡的过程,我们就需要在以往的树的结构的代码上做点修改,定义一个指针指向节点的父亲。
树的结构体定义和一些宏;
#define NOT_INIT 0//没有初始化的标志
#define HAVE_BEEN_INIT 1//初始化了的标志
#define TRUE 1
#define FALSE 0
#define m 3//B树的阶
typedef struct BTreeNode{
KeyType key[m + 1];//关键字数组 0号元素不用 m是最大元素个数
struct BTreeNode* ptr[m + 1];//从0开始指向子树的指针
struct BTreeNode* parent;//指向父级的指针
int keynum;//当前节点中关键字的个数 也就是节点的大小
}BTnode, *BTree;//B树节点的类型和根节点(树)的类型代码实现(建议先把逻辑理顺后再看)
代码实现在逻辑的基础上还需要考虑各种可能的复杂情况,根据上文的举例,这里总结出执行插入的大致框架(画的不是很好,但是大概意思就是这样):
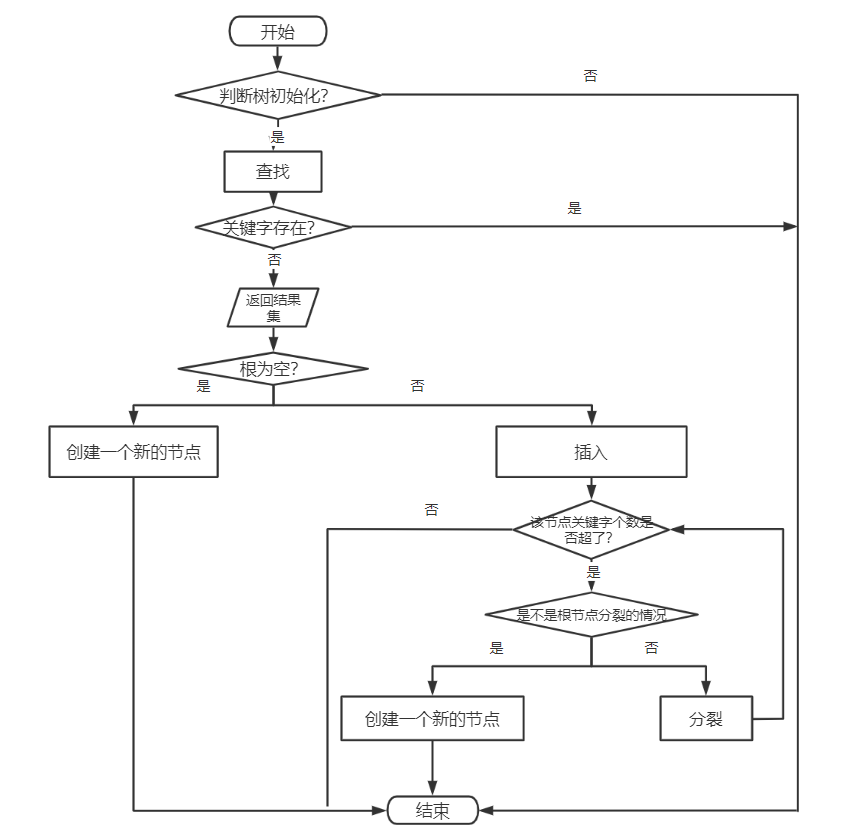
为方便大家理解代码,这里代码的顺序是按照流程图上的顺序来的,实际上应该把顺序反过来或者在前面声明。
/*初始化一棵树*/
void initBTreeOperation(BTree& tree)
{
if (status == HAVE_BEEN_INIT)
{
//已经初始化过了
printf("已经初始化过了\n");
}
else
{
tree = NULL;
status = HAVE_BEEN_INIT;
}
}
/*在B树中插入一个值 */
void insertKeyOperation(BTree& tree, KeyType key)
{
Result r;//封装结果集
if (status == NOT_INIT)
{
//树没有初始化
printf("请先初始化\n");
return;
}
if (tree == NULL)
{
//此时树是空树
printf("树是空树\n");
}
//如果是索引 不允许重复的情况
//查找有没有相同的值
searchNode(tree, key, r);
if (r.tag == 1)
{
//关键字已经存在
printf("关键字已经存在\n");
}
else
{
//执行插入操作
insertBTree(tree, key, r.pt, r.i);
}
}
/*
在B树tree中q节点相关的位置 i - 1 ~ keynum 之间插入关键字
*/
void insertBTree(BTree& tree, KeyType key, BTree q, int i)//q和i是封装好的节点和下标
{
BTree temp;
int finished = FALSE;//表示循环完结状态的变量
int isNeed_NewNode = FALSE;//表示是否需要创建一个新的节点
//此时父节点是空的
if (q == NULL)
{
//代表这个树连根都没有
//创建一个新的节点
newRoot(tree, NULL, NULL, key);
}
else
{
//整体的插入
temp = NULL;
//插入从上往下插入 不需要递归 只需要循环 没有回溯
//finished标志的变化只存在于现有的节点数量里插入
//如果需要新的节点插入没有结束 需要判断是否需要创建一个新的节点
while(finished == FALSE && isNeed_NewNode == FALSE)
{
//肯定是先插入 将关键字和temp 插入q的q->key[i]和q->ptr[i]
insert(q, i, key, temp);
//插入完以后判断 如果q的关键字个数小于最大个数m 说明树的结构没有改变
if (q->keynum < m)
{
finished = TRUE;
}
//否则就要拆分
else
{
//先找中间位置
int s = (m + 1) / 2;
split(q, s, temp);
//还要向父级插入s的关键字
key = q->key[s];
if (q->parent != NULL)
{
//往双亲的位置插入s关键字
q = q->parent;
i = search(q, key);
}
else
{
//如果双亲节点为空 说明要新建一个节点
isNeed_NewNode = TRUE;
}
}
}
//如果需要创建一个新的节点
if (isNeed_NewNode == TRUE)
{
newRoot(tree, q, temp, key);
}
}
}
/*
将关键字和temp 插入q的q->key[i]和q->ptr[i]
q是插入的目标节点 i是位序 key是关键字 ap是新节点的指针
*/
void insert(BTree& q, int i, KeyType key, BTree ap)
{
for (int j = q->keynum; j >= i; j--)
{
//将数组后移
q->key[j + 1] = q->key[j];
q->ptr[j + 1] = q->ptr[j];
}
q->key[i] = key;
q->ptr[i] = ap;
if (ap != NULL)
{
ap->parent = q;
}
q->keynum++;
}
/*
分裂步骤
将q节点分裂成两个节点 前一半不动 后一半放进新节点ap中 s是中间位序
*/
void split(BTree& q, int s, BTree ap)
{
ap = (BTree)malloc(sizeof(BTnode));
ap->ptr[0] = q->ptr[s];
for (int i = s + 1, j = 1; i <= q->keynum; i++, j++)
{
ap->key[j] = q->key[i];
ap->ptr[j] = q->ptr[i];
}
ap->keynum = q->keynum - s;
ap->parent = q->parent;
//ap的孩子的父节点也要更新
for (int i = 0; i <= ap->keynum; i++)
{
if (ap->ptr[i] != NULL)
{
ap->ptr[i]->parent = ap;
}
}
q->keynum = s - 1;
}
/*生成新的根节点*/
void newRoot(BTree& tree, BTree p, BTree q, KeyType key)//pq是tree的左右孩子
{
tree = (BTree)malloc(sizeof(BTnode));
tree->keynum = 1;
tree->key[1] = key;
tree->ptr[0] = p;
tree->ptr[1] = q;
//别忘记处理孩子的父级指针
if (p != NULL)
{
p->parent = tree;
}
if (q != NULL)
{
q->parent = tree;
}
tree->parent = NULL;//别忘记根也有父级 只不过是NULL
}个人为如果把逻辑理顺了,再结合流程图去理解,插入和分裂的代码肯定是没问题了的,那么接下来是删除操作。
四、删除
对于B树的删除我们同样需要分成三种情况:
情况一:如果待删除数据data在节点x中,并且x是叶子节点,直接删除;
情况二:如果待删除的数据data在节点x中,并且是内部的节点,这时候又分为三种情况:
①如果data的前第一个孩子y至少有最小关键字个数+1个数据,找data的直接前驱p,删除data,并用p换掉data;

当我们要删除的数据是G时,发现G所在的节点是内部节点x,如果直接删除G,那么x的关键字个数与其孩子的个数就会矛盾,为了使操作尽可能的简单,我们发现G的左孩子y的关键字个数明显大于最小关键字个数+1个数据,这时用节点y的最后一个关键即G的直接前驱F替换G,既不会影响x节点的平衡,又不会影响y节点的平衡,还保证了关键字的有序性;
②如果y节点已经是最小元素个数了,找data的后第一个孩子z至少最小关键字个数+1个数据,找data的直接后继q,删除data,并用q换掉data;

情况②与情况①的意思是一样的,如果节点x的左孩子关键字个数小于最小关键字个数+1个数据,为了保持x与它孩子的性质不改变,这时判断x的右孩子z的关键字个数是否大于最小关键字个数+1个数据,如果大于就向节点z“借”,同样不会影响x节点的平衡,也不会影响z节点的平衡,还保证了关键字的有序性;
③如果前后都不够,就合并y和z;

假设完成某些操作后的树如上所示,此时再删除关键G,会发现它的左孩子关键字只剩下D,而它的右孩子关键字只剩下了K,左右孩子都不够借的,就把D所在的节点y和K所在的节点z合并,这一步和插入中的分裂操作正好相反,但是意义是一样的;
情况三:修正;
很明显情况一、二只能保证当前节点的平衡不被破坏,但是删除导致的后果可能是多个节点的平衡被破坏,这时候就需要再去对整棵树进行修正。
如果当待删除数据data不再是内部节点,那么它一定在子树c上,且此时c也只有最小关键字个元素时,也分为两种情况:
情况①:和内部节点一样,如果c的兄弟至少有最小关键字个数+1个数据,将x的某一数据下移,c兄弟的某一数据上移到父节点x;

当我们要删除数据B时,发现B所在的节点是实际中的叶子节点c,且删除B之后c的关键字个数已经小于最小关键字个数,这时c的兄弟的关键字个数大于最小关键字个数+1,就将父节点x的对应的关键字下移,将兄弟节点的第一个关键字上移(此时兄弟节点是右兄弟的情况),如此也不会破坏父节点、当前节点和兄弟节点的平衡;
因为是修正操作,所以不光要检测当前节点,还要检测当前节点的父节点、一直到根节点,持续向上地修正,从而保证整棵树的性质;
情况②:如果c和它的兄弟都只包含最少,就合并;

叶子的合并的操作和内部节点的合并是一样的,就不再过多描述了,最后也需要向上修正;
学到这里可能会点懵:什么又是内部节点又是叶子的、什么合并什么旋转啊...不要慌,这说明你在思考了。其实从整体来看B树的删除无非就是内部节点的删除和叶子节点的删除,它们之间的区别就在于当删除节点的兄弟有多的关键字时,旋转(借关键字)的步骤有些差异,而合并操作其实是一样的;并且只要理顺:插入和删除其实都是在实际的叶子中进行的,然后不断向上检测平衡性就行了。
代码实现(建议先把逻辑理顺后再看)
当然在代码中我们需要考虑到的情况要更多更复杂,但是基本的逻辑是没有变的,这里同样大致总结了一下删除的整体流程(仅供参考,以逻辑为准):
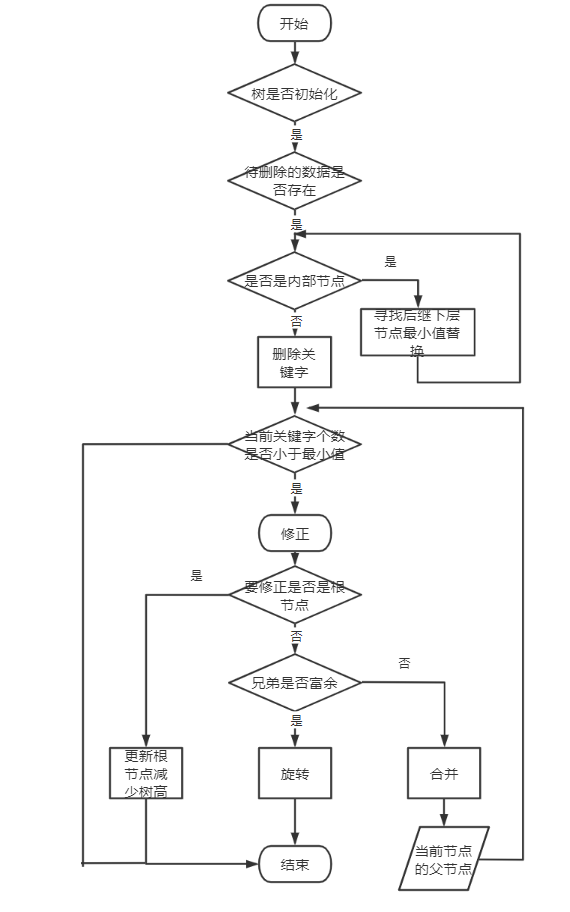
为了和流程图对照上,这里还和插入一样更改了代码的顺序:
/*封装删除操作*/
void deleteKeyOperation(BTree& tree, KeyType key)
{
Result r;
if (status == NOT_INIT)
{
//树没有初始化 请先初始化
printf("请先初始化\n");
}
if (tree == NULL)
{
//此时树是空树
printf("树是空树\n");
}
else
{
searchNode(tree, key, r);
if (r.tag == 1)
{
//如果是1说明查找到了 可以删除 和 插入正好相反
//需要执行删除操作
deleteBTree(tree, r.pt, r.i);
}
else
{
//关键字不存在
printf("找不到该关键字\n");
}
}
}
/*
删除tree上p节点的第i个关键字
*/
void deleteBTree(BTree& tree, BTree& p, int i)
{
if (p->ptr[i] != NULL)//不是叶子节点 是内部节点时
{
//找到后继的下层内部节点的最小关键字来替换
successor(p, i);
//删除最下层的非叶子节点的最小关键字
deleteBTree(tree, p, 1);
}
else
{
//从节点p中删除key[i]
removeNode(p, i);
//判断是否需要调整Btree 看当前关键字是否小于最少关键字
if (p->keynum < (m - 1) / 2)//上界和下界都是人为定义的
{
restore(tree, p);
}
}
}
/*找到后继的下层内部节点的最小关键字来替换*/
void successor(BTree& p, int i)
{
BTree leaf = p;
if (p == NULL)
{
return;
}
leaf = leaf->ptr[i];//指向子树
while (leaf->ptr[0] != NULL)//只要还有孩子 就继续往下走
{
leaf = leaf->ptr[0];
}
p->key[i] = leaf->key[1];
p = leaf;
}
/*移除节点 从后往前覆盖*/
void removeNode(BTree& p, int i)
{
for (int j = i; j < p->keynum; j++)
{
p->key[j] = p->key[j + 1];
p->ptr[j] = p->ptr[j + 1];
}
p->keynum--;
}
/*调整树 p是要调整的节点*/
void restore(BTree& tree, BTree& p)
{
BTree parent, leftBrother, rightBrother;//p的父节点、和左右兄弟
parent = p->parent;
//如果父节点不为空的情况 就是不是根节点的情况
if (parent != NULL)
{
//寻找左右兄弟 向兄弟借值
//先要找到p节点在父节点的哪一个孩子
int i;
for (i = 0; i < parent->keynum; i++)
{
if (parent->ptr[i] == p)
{
break;
}
}
//如果p是最左边的孩子 就不需要找左边的兄弟了 右边同理
if (i > 0)
{
leftBrother = parent->ptr[i - 1];
}
else
{
leftBrother = NULL;
}
if (i < parent->keynum)
{
rightBrother = parent->ptr[i + 1];
}
else
{
rightBrother = NULL;
}
//如果左右兄弟有富余 就借
if ((leftBrother != NULL && leftBrother->keynum >= (m + 1) / 2) ||
(rightBrother != NULL && rightBrother->keynum >= (m + 1) / 2))
{
borrowFromBro(p, parent, leftBrother, rightBrother, i);
}
//如果左右兄弟都没有富余 就合并
else
{
if (leftBrother != NULL)
{
//和左兄弟合并
mergeWithLeftBro(tree, p, leftBrother, parent, i);
}
else if (rightBrother != NULL)
{
//和右兄弟合并
mergeWithRightBro(tree, p, rightBrother, parent, i);
}
//如果当左右子树不存在时
else
{
//改变根节点
for (int j = 0; j <= parent->keynum + 1; j++)
{
if (parent->ptr[j] != NULL)
{
tree = parent->ptr[j];
break;
}
tree->parent = NULL;
}
}
}
}
else
{
BTree temp;
//父节点为空的情况 p就是根节点
//去掉父节点 使树减一层
for (int j = 0; j <= p->keynum; j++)
{
if (p->ptr[j] != NULL)
{
temp = p;
p = p->ptr[j];
temp->ptr[j] = NULL;
free(temp);
break;
}
}
tree = p;
tree->parent = NULL;
}
}
/*向左兄弟或者右兄弟去借关键字*/
void borrowFromBro(BTree& p, BTree& parent, BTree& leftBrother, BTree& rightBrother,int i)
{
//向左兄弟借 左兄弟的值都小于p的值 所以要把p的值右移
if (leftBrother != NULL && leftBrother->keynum >= (m + 1) / 2)
{
for (int j = p->keynum + 1; j > 0; j--)
{
if (j > 1)
{
p->key[j] = p->key[j - 1];
}
p->ptr[j] = p->ptr[j - 1];
}
p->ptr[0] = leftBrother->ptr[leftBrother->keynum];
if (p->ptr[0 != NULL])
{
p->ptr[0]->parent = p;
}
leftBrother->ptr[leftBrother->keynum] = NULL;
//被删除节点p要存父节点的关键字
p->key[1] = parent->key[i];
//父节点的关键字变成左兄弟的最大
parent->key[i] = leftBrother->key[leftBrother->keynum];
//当前节点关键字加一 左兄弟节点关键字减一
leftBrother->keynum--;
p->keynum++;
}
else if (rightBrother != NULL && rightBrother->keynum >= (m + 1) / 2)
{
p->key[p->keynum + 1] = parent->key[i + 1];
//子树指针指向右兄弟最小的子树的指针
p->ptr[p->keynum + 1] = rightBrother->ptr[0];
if (p->ptr[p->keynum + 1] != NULL)
{
p->ptr[p->keynum + 1]->parent = p;
}
p->keynum++;
//父节点向右兄弟要关键字
parent->key[i + 1] = rightBrother->key[1];
//将右兄弟的关键字向左移
for (int j = 0; j <= rightBrother->keynum; j++)
{
if (j > 0)
{
rightBrother->key[j] = rightBrother->key[j + 1];
}
rightBrother->ptr[j] = rightBrother->ptr[j + 1];
}
rightBrother->ptr[rightBrother->keynum] = NULL;
rightBrother->keynum--;
}
}
/*和左兄弟合并*/
void mergeWithLeftBro(BTree& tree, BTree& p, BTree& leftBrother, BTree& parent, int i)
{
//先把父节点的第i个关键字拿下
leftBrother->key[leftBrother->keynum + 1] = parent->key[i];
leftBrother->ptr[leftBrother->keynum + 1] = p->ptr[0];
if (leftBrother->ptr[leftBrother->keynum + 1] != NULL)
{
leftBrother->ptr[leftBrother->keynum + 1]->parent = leftBrother;
}
leftBrother->keynum++;
//再把p中的关键字一个个赋给左兄弟
for (int j = 1; j <= p->keynum; j++)
{
leftBrother->key[leftBrother->keynum + j] = p->key[j];
leftBrother->ptr[leftBrother->keynum + j] = p->ptr[j];
if (leftBrother->ptr[leftBrother->keynum + j] != NULL)
{
leftBrother->ptr[leftBrother->keynum + j]->parent = leftBrother;
}
}
leftBrother->keynum += p->keynum;
parent->ptr[i] = NULL;
free(p);
//还要对父节点进行左移
for (int j = i; j <= parent->keynum; j++)
{
parent->key[j] = parent->key[j + 1];
parent->ptr[j] = parent->ptr[j + 1];
}
parent->ptr[parent->keynum] = NULL;
parent->keynum--;
//还要检查父节点是不是违反了规则
//如果父节点是根节点
if (tree == parent)
{
//当根节点没有关键字的时候 才进行调整
if (parent->keynum == 0)
{
for (int j = 0; j <= parent->keynum + 1; j++)
{
if (parent->ptr[j] != NULL)
{
tree = parent->ptr[j];
break;
}
tree->parent = NULL;
}
}
}
else
{
//如果不是根节点 就判断是否需要重新进行调整
if (parent->keynum < (m - 1) / 2)
{
restore(tree, parent);
}
}
}
/*和右兄弟合并*/
void mergeWithRightBro(BTree& tree, BTree& p, BTree& rightBrother, BTree& parent, int i)
{
//先要把右兄弟的关键字右移 为p的关键字和父节点的关键字空位
for (int j = rightBrother->keynum; j > 0; j--)
{
if (j > 0)
{
//为p的关键字和父节点的关键字空位
rightBrother->key[rightBrother->keynum + 1 + p->keynum] = rightBrother->key[j];
}
rightBrother->ptr[rightBrother->keynum + 1 + p->keynum] = rightBrother->ptr[j];
}
//把父节点的那一个关键字拿下
rightBrother->key[p->keynum + 1] = parent->key[i + 1];
//再把p中的关键字一个个赋给右兄弟
for (int j = 0; j <= p->keynum; j++)
{
if (j > 0)
{
//为p的关键字和父节点的关键字空位
rightBrother->key[j] = p->key[j];
}
rightBrother->ptr[j] = p->ptr[j];
if (rightBrother->ptr[j] != NULL)
{
rightBrother->ptr[j]->parent = rightBrother;
}
}
rightBrother->keynum += p->keynum + 1;
parent->ptr[i + 1] = NULL;
free(p);
for (int j = i + 1; j <= parent->keynum; j++)
{
parent->key[j] = parent->key[j + 1];
parent->ptr[j] = parent->ptr[j + 1];
}
//如果父节点在关键字减少之前只有一个节点 就需要把父节点的右孩子赋值给左孩子
if (parent->keynum == 1)
{
parent->ptr[0] = parent->ptr[1];
}
parent->ptr[parent->keynum] = NULL;
parent->keynum--;
//还要对父节点进行左移
for (int j = i; j <= parent->keynum; j++)
{
parent->key[j] = parent->key[j + 1];
parent->ptr[j] = parent->ptr[j + 1];
}
parent->ptr[parent->keynum] = NULL;
parent->keynum--;
//还要检查父节点是不是违反了规则
//如果父节点是根节点
if (tree == parent)
{
//当根节点没有关键字的时候 才进行调整
if (parent->keynum == 0)
{
for (int j = 0; j <= parent->keynum + 1; j++)
{
if (parent->ptr[j] != NULL)
{
tree = parent->ptr[j];
break;
}
tree->parent = NULL;
}
}
}
else
{
//如果不是根节点 就判断是否需要重新进行调整
if (parent->keynum < (m - 1) / 2)
{
restore(tree, parent);
}
}
}后记
至此,第一棵高阶搜索树B树就结束了,其实理顺了逻辑会发现并不难,只是需要考虑的情况很多很复杂,但是慢慢啃一定能学会的!因为提到过B树是要与磁盘做交互才能体现出其优越性,而本文的重点在于讲清B树增删查改的逻辑,所以就没有main函数的测试了,作为初学者的我们只需要能够理解理顺它的思想、逻辑和代码就足够了;
我自认为每一句代码都有过详细的注释了,但是一定一定一定要理顺逻辑再去看代码(重要的事情说N遍)如果对于代码还有疑问的欢迎与我联系!