欠定方程组的最小范数解（超曲面和原点的距离，原点球心球面和超曲面的切点）

今天小白问了我一个问题，我觉得颇有意思，做个记录。

问题描述

小白：插入一个问题，这个切点怎么求？就是固定超平面Ax=b 怎么求它的最小二范数。

她说得不是很清楚，我再翻译一下。几何的提法是，超平面 $Ax=b$ 到圆心距离是多少？代数的提法是，欠定方程组 $Ax=b$ 的最小范数解是什么？

问题建模

我喜欢代数这个提法。重新描述一下，我们考虑
$$y=Ax$$
这里的 $A\in {\mathbf{R}}^{m\times n}$ 是个 胖矩阵，即 $m<n$。我们不妨假定 $A$ 是行满秩的。
对于这个问题，我们知道这里未知量的个数比方程的个数多，也就是解是存在不唯一的。代数学知识告诉我们，它的解集是
{ x ∣ A x = y } = { x p + z ∣ z ∈ N ( A ) } \{x \mid A x=y\}=\left\{x_{p}+z \mid z \in \mathcal{N}(A)\right\} { x∣Ax=y}={ xp​+z∣z∈N(A)}
这里 $x_p$ 是个特解。零空间的维数 $\mathcal{N}(A)=n-m$ 刻画了自由度的数目。那么，我们能否选择一个 $z$ ，使得 $x_p+z$ 的二范数最小呢？

问题解答

这是个经典的计算数学问题了，如果是低于三维的情况，高中的知识很快就能解出来了。高维情况，答案也很简单，他就是
$$x_{\ln }=A^T{\left(A{A}^T\right)}^{-1}y$$
因为 A 是行满秩的，所以 $A{A}^T$ 是可逆的。怎么得到的这个解？对于
$$Ax=b$$
我们令 $x=A^T\bar{x}$，$\bar{x}$ 是个 m 维的。则有
$$x=A^T\bar{x}=A^T(A{A}^T{)}^{-1}b.$$
事实上，这个 $x_{\ln }$ 就是最小范数解，它极小化了如下的优化问题，

minimize $\Vert x\Vert$
subject to $Ax=y$

其中，$x\in {\mathbf{R}}^n$。证明如下：

假定其它解满足 $Ax=y$，那么 $A\left(x-x_{\ln }\right)=0$，且
$$\begin{array}{rl}{\left(x-x_{\ln }\right)}^T{x}_{\ln }& ={\left(x-x_{\ln }\right)}^T{A}^T{\left(A{A}^T\right)}^{-1}y\\ & ={\left(A\left(x-x_{\ln }\right)\right)}^T{\left(A{A}^T\right)}^{-1}y\\ & =0\end{array}$$
也就是说，$\left(x-x_{\ln }\right)\perp x_{\ln }$，那么
$$\Vert x{\Vert }^2={\Vert x_{\ln }+x-x_{\ln }\Vert }^2={\Vert x_{\ln }\Vert }^2+{\Vert x-x_{\ln }\Vert }^2\ge {\Vert x_{\ln }\Vert }^2$$
说明了 $x_{\ln }$ 是范数最小的解。

$A^{†}:=A^T{\left(A{A}^T\right)}^{-1}$ 叫做行满秩胖矩阵 $A$ 的伪逆，实际上是 $A$ 的右逆。

几何观点

画个示意图如下，

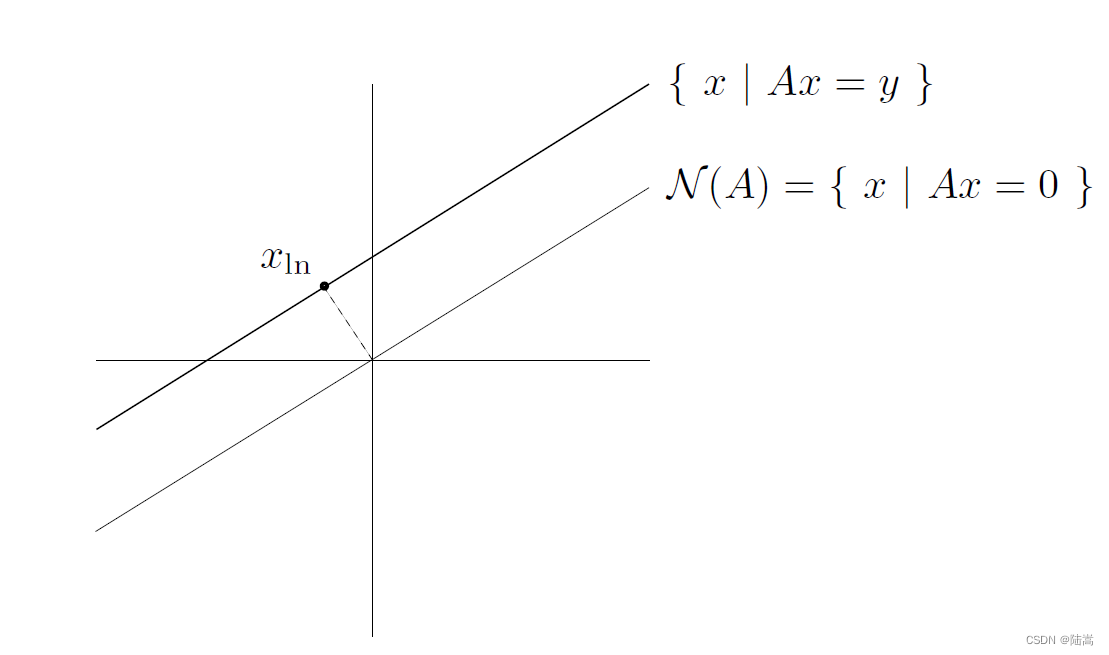
• 这个解垂直于零空间，$x_{\ln }\perp \mathcal{N}(A)$。
• 这个解是 0 在解空间上的投影。

超定方程组的最小范数解

虽然主题是欠定方程组，但对于超定方程组
$$Ax=b$$
我们左乘 $A^T$，可以得到 $A^{T}Ax=A^{T}b$，则我们得到胖矩阵的伪逆 $A^{†}={\left(A^{T}A\right)}^{-1}{A}^T$，它实际上是 $A$ 的左逆。容易证明，它也是满足最小二乘误差相同的最小范数解。

QR 分解表示

我们找 $A^T$ 的 QR 分解，满足 $A^T=QR$，且

• $Q\in {\mathbf{R}}^{n\times m},Q^{T}Q=I_m$
• $R\in {\mathbf{R}}^{m\times m}$ 是个非奇异的上三角矩阵，那么，我们得到一个更简单的表达
  $$x_{\ln }=A^T{\left(A{A}^T\right)}^{-1}y=Q{R}^{-T}y$$
  且 $\Vert x_{\ln }\Vert =\Vert R^{-T}y\Vert$。

拉格朗日乘子法推导

除了上述的分裂法推导外，我们也可以用拉格朗日乘子法得到这个最小范数解。

最小范数解无非是求解如下优化问题，

minimize $x^{T}x$
subject to $Ax=y$

引入拉格朗日乘子，
$$L(x,\lambda )=x^{T}x+{\lambda }^T(Ax-y)$$
最优性条件是，
$${\nabla }_{x}L=2x+A^T\lambda =0,{\nabla }_{\lambda }L=Ax-y=0$$

从第一个条件，我们可以得到 $x=-A^T\lambda /2$，把它代入第二个条件，我们有 $\lambda =-2{\left(A{A}^T\right)}^{-1}y$，因此
$$x=A^T{\left(A{A}^T\right)}^{-1}y$$

和正则最小二乘的关系

定义 $J_1=\Vert Ax-y{\Vert }^2,J_2=\Vert x{\Vert }^2$，最小化加权目标函数
$$J_1+\mu J_2=\Vert Ax-y{\Vert }^2+\mu \Vert x{\Vert }^2$$
可得
$$x_{\mu }={\left(A^{T}A+\mu I\right)}^{-1}{A}^{T}y$$
那么正则最小二乘解其实是收敛到最小范数解的，即当 $\mu \to 0$，我们有
$${\left(A^{T}A+\mu I\right)}^{-1}{A}^T\to A^T{\left(A{A}^T\right)}^{-1}$$

更一般的等式约束范数极小化框架

考虑问题

minimize $\Vert Ax-b\Vert$
subject to $Cx=d$

这个问题包含了上述的最小范数和最小二乘问题。它等价于

minimize $(1/2)\Vert Ax-b{\Vert }^2$
subject to $Cx=d$

拉格朗日乘子是
$$\begin{array}{rl}L(x,\lambda )& =(1/2)\Vert Ax-b{\Vert }^2+{\lambda }^T(Cx-d)\\ & =(1/2)x^T{A}^{T}Ax-b^{T}Ax+(1/2)b^{T}b+{\lambda }^{T}Cx-{\lambda }^{T}d\end{array}$$
最优性条件是，
$${\nabla }_{x}L=A^{T}Ax-A^{T}b+C^T\lambda =0,{\nabla }_{\lambda }L=Cx-d=0$$
写成块矩阵的形式，
$$\left[\begin{array}{cc}{A}^{T}A& C^T\\ C& 0\end{array}\right]\left[\begin{array}{l}x\\ \lambda \end{array}\right]=\left[\begin{array}{c}{A}^{T}b\\ d\end{array}\right]$$
如果块矩阵是可逆的，我们有
$$\left[\begin{array}{l}x\\ \lambda \end{array}\right]={\left[\begin{array}{cc}{A}^{T}A& C^T\\ C& 0\end{array}\right]}^{-1}\left[\begin{array}{c}{A}^{T}b\\ d\end{array}\right]$$
进一步，如果 $A^{T}A$ 是可逆的，我们有更加漂亮的写法，从第一块我们可以得到
$$x={\left(A^{T}A\right)}^{-1}\left(A^{T}b-C^T\lambda \right)$$
代入 $Cx=d$ 可得
$$C{\left(A^{T}A\right)}^{-1}\left(A^{T}b-C^T\lambda \right)=d$$
因而
$$\lambda ={\left(C{\left(A^{T}A\right)}^{-1}{C}^T\right)}^{-1}\left(C{\left(A^{T}A\right)}^{-1}{A}^{T}b-d\right)$$
那么 $x$ 就可以不太优雅地表达为
$$x={\left(A^{T}A\right)}^{-1}\left(A^{T}b-C^T{\left(C{\left(A^{T}A\right)}^{-1}{C}^T\right)}^{-1}\left(C{\left(A^{T}A\right)}^{-1}{A}^{T}b-d\right)\right)$$

复习 KKT

很多人把优化忘记了，我们复习一下 KKT 系统相关。
考虑问题
min ⁡ x ∈ R n f ( x )  subject to  c i ( x ) = 0 , i ∈ E = { 1 , … , m e } c i ( x ) ≥ 0 , i ∈ I = { m e + 1 , … , m } \begin{array}{ll} \min _{x \in \mathbb{R}^{n}} & f(x) \\ \text { subject to } & c_{i}(x)=0, \quad i \in \mathcal{E}=\left\{1, \ldots, m_{e}\right\} \\ & c_{i}(x) \geq 0, \quad i \in \mathcal{I}=\left\{m_{e}+1, \ldots, m\right\} \end{array} minx∈Rn​ subject to ​f(x)ci​(x)=0,i∈E={ 1,…,me​}ci​(x)≥0,i∈I={ me​+1,…,m}​
它的拉格朗日函数是，
$$\mathcal{L}(x,\lambda )=f(x)-\sum _{i\in \mathcal{E}\cup \mathcal{I}}{\lambda }_i{c}_i(x)$$
那么，它的 KKT 条件可以写为
$$\begin{array}{rlrl}{\nabla }_x\mathcal{L}\left(x^{\ast },{\lambda }^{\ast }\right)& =0,& & \\ c_i\left(x^{\ast }\right)& =0,& & \forall i\in \mathcal{E}\\ c_i\left(x^{\ast }\right)& \ge 0,& & \forall i\in \mathcal{I}\\ {\lambda }_i^{\ast }& \ge 0,& & \forall i\in \mathcal{I}\\ {\lambda }_i^{\ast }{c}_i\left(x^{\ast }\right)& =0,& & \forall i\in \mathcal{E}\cup \mathcal{I}\end{array}$$
当然，这些条件都有一些奇奇怪怪的名字，比如“互补性条件”之类的，可以不用管。当然，如果只有等式约束，那么其实只有前两条，很简单，也很好记。如果有不等式约束，需要看一下最后两条的互补性。

代码

no code