//对于数据结构的学习,本笔记本所采用教材是《数据结构C++语言版》,作者是邓俊辉,配合邓老师的网课,虽然非常烧脑,但也十分有趣。
复杂度
评价不同算法的优劣,为做到客观公正,需要一个共同的模型和标尺,模型有图灵机和RAM(在这里不做详解,欲详细了解参考:
https://www.bilibili.com/video/av22774520/index_33.html#page=6)。标尺则是复杂度,分为时间复杂度和空间复杂度。本书把重点放在时间复杂度原理和方法的讲解上,空间复杂度基本相似,故而略过。
一把合格的尺子,需要有精确的度量刻度:big-O notation,big-Θ notation,big-Ω notation。三者分别是算法复杂度的上界,准确估计,和下界。算法的设计往往考虑的是最坏的情况,所以最常用的是作为复杂度上界的big-O notation。
先给出 big-O notation的定义:若存在正的常数c和函数f(n),使得对任何n>>2;都有
T(n) ≤ c*f(n)
则可认为在n足够大之后,f(n)给出了T(n)增长速度的一个渐进上界。此时,记为:
T(n) = O(f(n))
关于复杂度的问题,定义和分类并不重要,更为关键的是如何计算和优化,复杂度的优化和高等数学中求极限的过程有些相似,主要就是忽略常数项,低次项,以及系数,在这里不必多提。所以尤为重要的是,复杂度是如何计算的。(邓老师的书和视频里说的都有些跳脱,没有CS基础的笔者实在是听的云里雾里,希望本文这方面的总结尽量周全)
先考虑计算复杂度的具体步骤:
1.找出算法中的基本语句,在循环体中一般都是最内层循环的循环体;
2.计算基本语句的执行次数的数量级;(这个计算一般涉及高等数学的级数或者迭代计算,是对基本计算能力的考量)
3.用big-O notation表示算法的时间性能,即将基本语句执行次数的数量级放入big-O notation中。
知道了怎么做,那就要对具体做的是什么有一个归纳:
一般来说,算法中不存在循环语句,其时间复杂度就是O(1);常见的函数模型对应的复杂度如图所示:
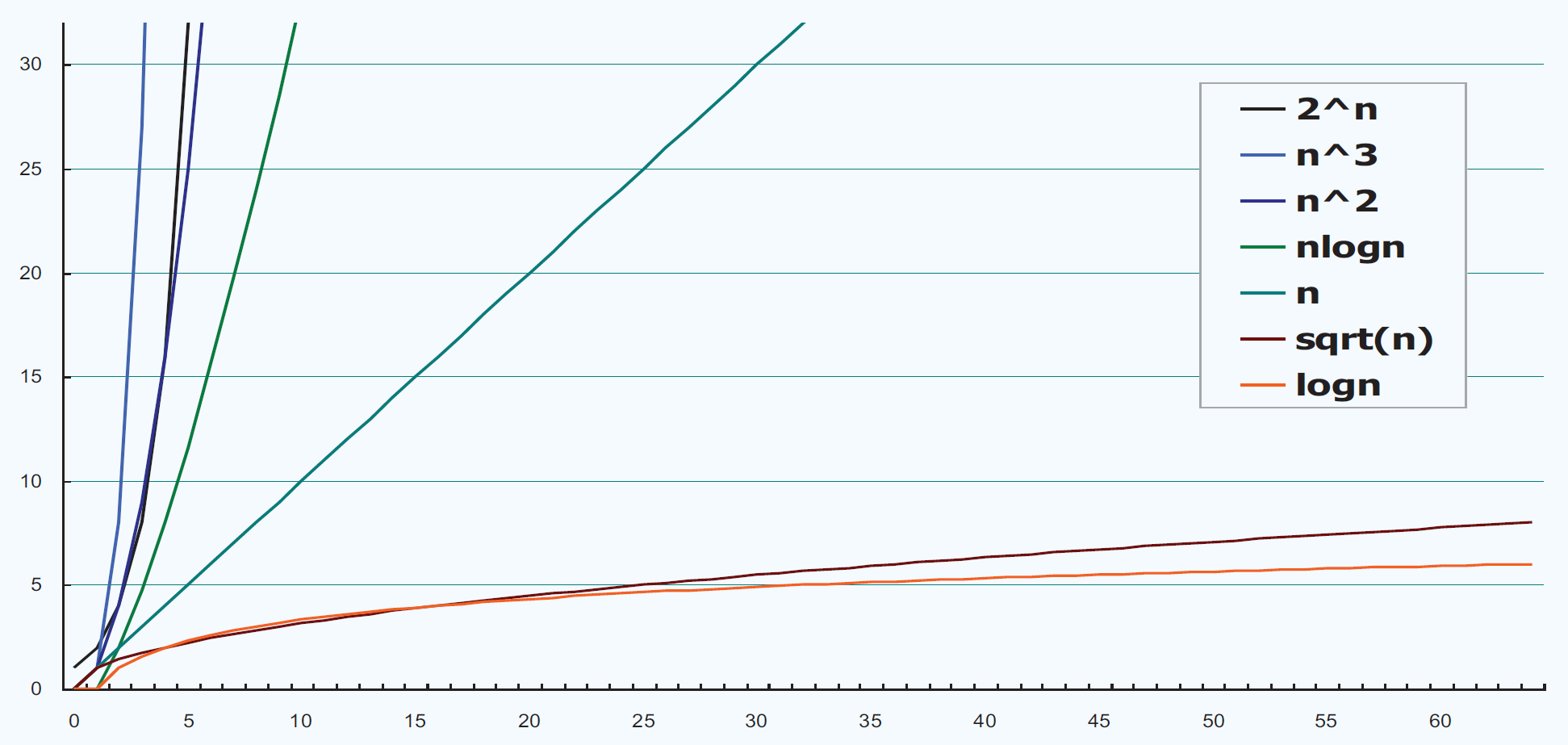
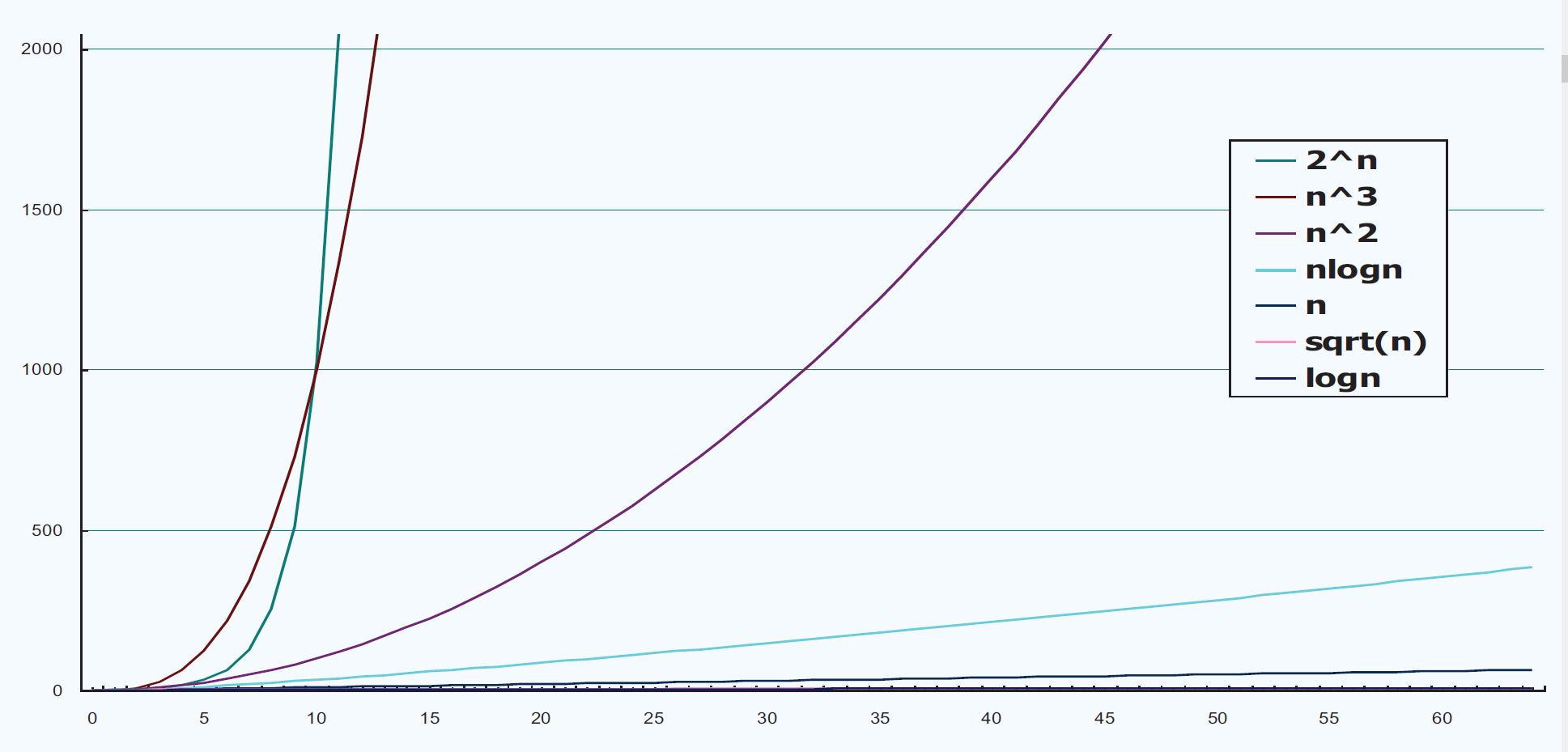
对于非O(2^n)和O(n!)的函数模型被称为多项式类型,其所费时间被称为多项式时间,O(2^n)和O(n!)二者所费时间则被称为指数时间。普遍认为,前者属于有效算法。
现在知道了计算流程和计算对象,再确立一些明确的计算法则:
1.简单的输入输出以及赋值语句,近似地认为需要O(1)时间;
2.对于顺序结构,存在big-O notation下的求和法则:若算法的2个部分时间复杂度分别为T1(n) = O(f(n))和T2(n) = O(g(n)),则T1(n)+T2(n) = O(max(f(n),g(n)))。请注意,若两部分为T1(m) = O(f(n))和T2(n) = O(g(n)),,则T1(m)+T2(n) = O(f(m)+g(n));
//看着似乎确实有些复杂,多做练习就好了
3.对于选择结构,如if语句,它的主要时间耗费再执行then语句或者else语句所用的时间,但是检验条件也需要O(1)时间;
4.对于循环结构,主要体现再多次迭代中执行循环体以及检验循环条件的时间耗费上面。此处可以推出复杂度计算的乘法法则:若算法2部分时间复杂度分别为T1(n) = O(f(n))和T2(n) = O(g(n)),则T1*T2 = O(f(n)*g(n));
5.若g(n) = O(f(n)),则O(f(n))+O(g(n)) = O(f(n));
6.O(cf(n)) = O(f(n)),其中c是一个正常数。
递归
“古之欲明明德于天下者,先治其国;欲治其国者,先齐其家;欲齐其家者,先修其身;欲修其身者,先正其心;欲正其心者,先诚其意;欲诚其意者,先致其知,致知在格物。物格而后知至,知至而后意诚,意诚而后心正,心正而后身修,身修而后家齐,家齐而后国治,国治而后天下平。”
《大学》这句话道出了递归的本质,分而治之(divide amd conque)和减而治值之(decrease and conque)是使用递归思想解决问题的主要入手点。
所谓分而治之,无非治众如治寡,分数是也。将一个规模较大的问题划分为两个规模相当的自问题,分别求解子问题,由子问题的解得到原问题的解。如图:
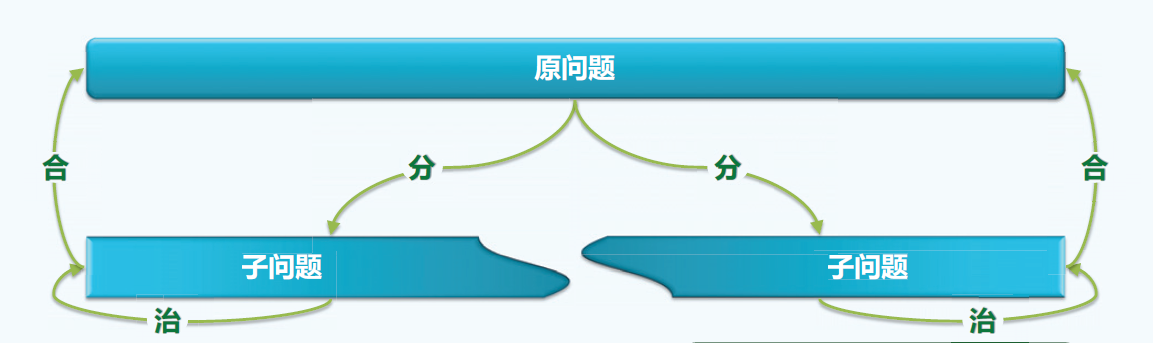
例:从数组区间A[lo,hi)中找出最大的两个整数A[x1]和A[x2],元素比较的次数要求尽可能的少。 //A[x1] ≥ A[x2]
void max2(int A[], int lo, int hi, int &x1, int &x2) {//1<n=hi - lo
for (x1 = lo, int i = lo + 1; i < hi; i++) //扫描A[lo,hi),找出A[x1]
if (A[x1] < A[i])
x1 = i;//hi - lo - 1 = n-1
for (x1 = lo, int i = lo + 1; i < x1; i++)//扫描A[lo, x1)
if (A[x2] < A[i])
x2 = i;//x1-lo-1
for (int i = x1 + 1; i < hi; i++)//再扫描A(x1,hi),找出A[x2]
if (A[x2] < A[i])
x2 = i;//hi - x1 - 1
所谓减而治之,笼统地说,就是将问题划分为两个完全不同量级的子问题,一个规模和原问题相近,另一个则是非常微末的子问题,同样分别求解子问题,然后由子问题的解得到原问题的解。如图:
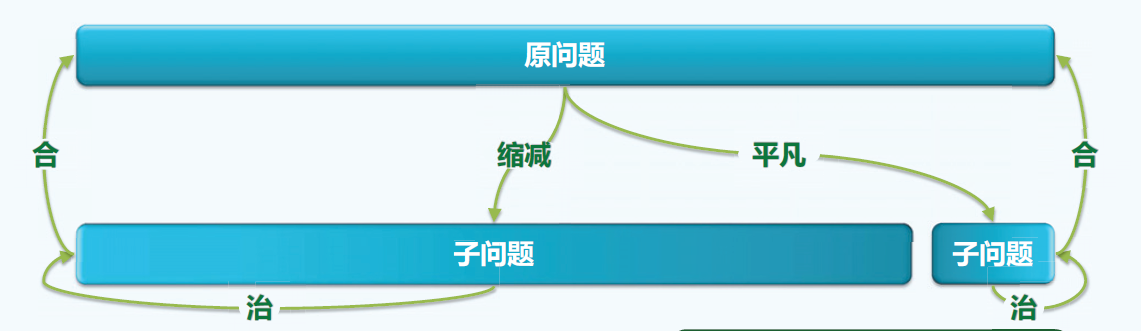
//减而治值的例子相对简单,此处略,详见讲义P71。
对于递归算法,常用的两个工具分别是:递归跟踪和递推公式。
递归跟踪(recursion trace):一种直观可视的方法,可用于分析递归算法的总体运算时间与空间。按照下述原则,将递归算法的执行过程整理为图的形式:
1.算法的每一递归实例都表示为一个方框,其中注明了该实例调用的参数;
2.若实例M调用实例N,则在M与N对应的方框之间添加一条有向联线
递推方程(recurrence equation):通过对递归模型的数学归纳,导出复杂度定界函数的递推方程组及其边界条件,从而将复杂度的分析,转换为递推方程组的求解。(类似于求解微分方程)