量化策略开发，高质量社群，交易思路分享等相关内容

导论与介绍

大家好，我是Le Chiffre

今天我们来为大家分享金融计量学系列内容，在松鼠量化3年多分享的内容中，大部分以量化策略为主，至今为止，我们已经发布了期货策略80+，股票策略5+，数字货币策略5+。以及各种量化相关的研究文章等等。

但是，过往内容中很少分享学术内容，在与慕总多次沟通交流后，我们制定了一系列的学术内容分享，其中金融计量学就是我们的首秀。

一、内容大纲

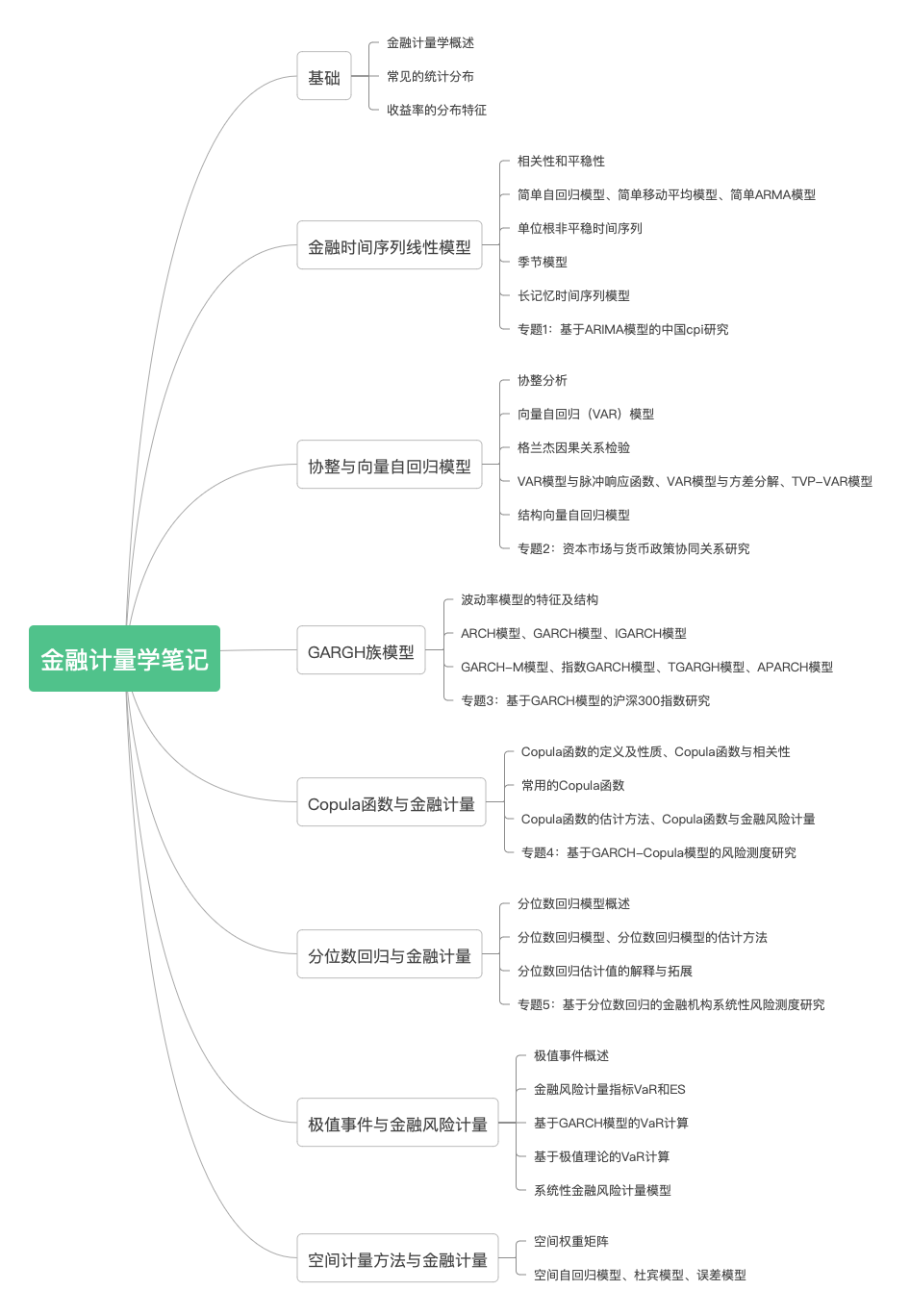
上述图片中是我们要分享的主要内容框架，但是大概率内容要更多一些。

二、基础与开始

何为计量学？何为金融计量学？

计量学(Econometrics)是应用统计学的方法对经济数据进行定量和定性分析的学科。它利用统计学的理论和方法,分析经济变量之间的关系,验证经济理论,并进行经济预测和决策。

计量学的主要任务有:1. 经济数据的收集和整理。收集各种经济数据和信息,整理成可用于分析的形式。2. 经济变量之间相关性的度量。使用相关系数、回归分析等统计方法分析经济变量之间的关系。3. 经济理论的验证。构建理论模型,并使用实证数据进行验证,判断理论模型是否符合实际情况。4. 经济预测和决策分析。利用历史数据建立预测模型,预测关键经济变量的未来走势,为经济决策提供参考。

总之,计量学是应用统计学的方法和模型对经济现象进行定量分析和研究的学科。说完上面计量学的概念和大体工作内容，那么金融计量学就显而易见了，顾名思义即对金融数据进行统计分析和计量建模的一门学科。

1、建模步骤

第一步：收集数据

这一步不做过多介绍，你没数据什么也干不了，具体的一大堆学术话我就不再这里赘述了。

第二步：将问题模型化（量化）

在这一步中，这一步需要把金融经济理论、金融经济变量之间的关系通过建立模型表达出来。具体包括：选择变量、确定变量间的数学关系、拟定模型估计参数的数值范围。实际上，构建的金融模型不可能完全反映现实世界中的金融问题，只能相对于研究目的做出最大程度的估值近似。

第三步：确定估计方法。根据数据、模型和目标行数，选择合适的模型，建立数学表达式，代码复现和计算。

第四步：模型检验。上一步的初步估计结果需要进一步的检验，观察是否能合理描述数据，是否具有经济学意义。检验分为3个方面：统计检验、计量经济学检验和经济、金融意义检验。

统计检验目的在于检验模型参数估计值的可靠性，包括模型拟合优度检验、变量和显著性检验等。

计量经济学检验主要看是否符合计量经济学理论，包括序列相关性检验、异方差检验、多重共线性检验以及协整检验。

经济、金融意义检验将计量检验的结果与相应的经济理论或金融理论相比较，确定两者是否相符。这块相对主观一些。

三、收益率计算

大部分学术研究都是从资产价格的时间序列开始的，如标普500指数每天的收盘价、黄金与原油的每日价格等。但在金融计量上，使用更多的是资产收益率。其原因收益率序列统计特征良好、稳定，无量纲。

1、单期（多期）简单收益率

设是Pt是t时刻的资产价格，从t-1至t日，持有该资产的投资者的单期简单毛收益率(1+Rt)为： 

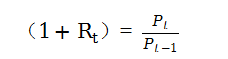
与之对应的简单单期净收益率为：    

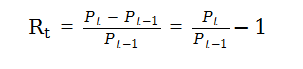
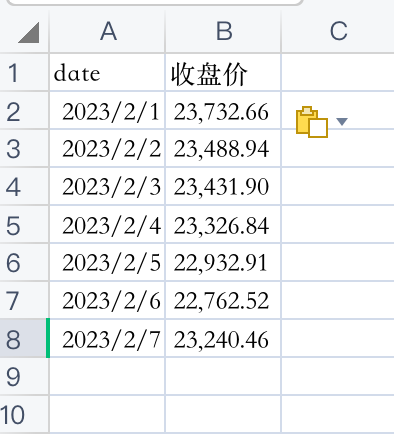
上表是2023年2月1日-7日比特币每日收盘价，当从t-n日至t日，持有n个周期资产，n期简单收益率为：

显然，n期简单收益率是其包含的这n期的单期简单毛收益率的乘积，也叫做复合收益率。

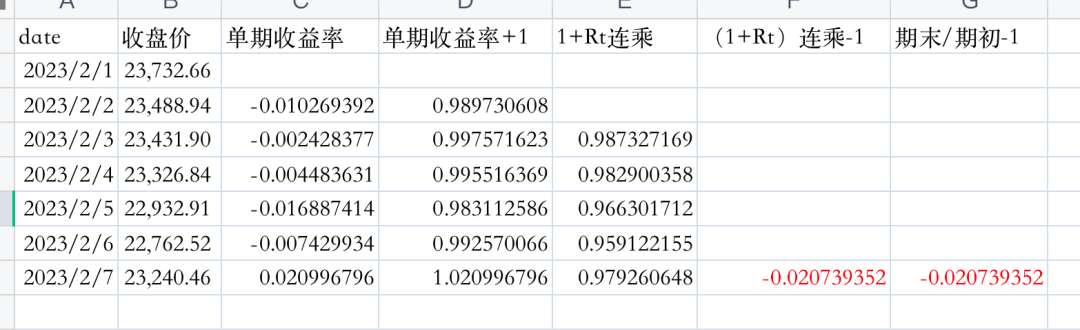
2、连续复利收益率

假设年收益率是10%, 1000元本金投资两年后的期末资金为1000*（1+10%）2=1210，若每年生息2次，则期末资金就是4次方，约为1215.5，若每年生息4次，则期末资金就是8次方，约为1218.4。

设年利率为r，初始资金为c，持有周期为n年，按照连续复利计算的资产终值A表示为：A=C*ern

如果是折现角度，那么就在e的r n次方前面加上一个“-”负号。

3、对数收益率

资产的简单毛收益率的自然对数成为对数收益率，也称为连续复合收益率：

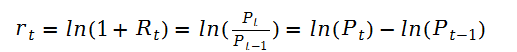
与简单收益率相比，对数收益率有诸多优点，因为对数化后可以直接进行加减操作。如上述公式等式最右边所示。

多期对数收益率是个单期对数收益率之和，在金融计量中，使用对数收益率不仅简化数学计算，而且简化了收益率统计特性的计量建模分析过程。

4、当期收益率与到期收益率

债券市场是金融市场的一个重要组成部分，在到期时，债务人会向债券的持有者支付票面价值或面值。有些债券定期会根据票面利率向投资者支付利息，有些债券不支付利息。到期支付全部票面金额的债券称为零息债券。债券收益率通常有当期收益率和到期收益率两种类型。

当期收益率指的是每年支付给投资者的收益的比例，表示为“

当期收益率 = （支付的年度利息额/债券的市场价格）*100%

例如，投资者购买价值90元的债券，债券面值为100，债券的票面利率为每年6%，则该投资者的当期收益率：

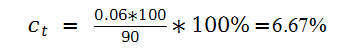
ct代表当期收益率，下表t表示t时刻的收益率，从当期收益率的定义来看，任何投资过程中的资本收益或损失都没有包含在当期收益率中。而零息债券不同于浮息债券，因为不付利息，因此计算方法如下：

当期收益率 =（面值/购买价格）1/t-1

t表示以年度计量的到期时间，例如：投资者购买价值80元零息债券，面值为100，该债券在两年内到期，则该债券的到期收益率为

Ct=(100/80)0.5-1

到期收益率表示债券的投资收益。简言之，到期收益率就是未来所有现金流的现值除以债券的价格，假设在购买日和到期日之间，投资者收到n期利息支付，y为债券的到期收益率，p为债券价格，f为债券的面值，为第i期的利息支付。则折现（或者叫贴现）公式为：

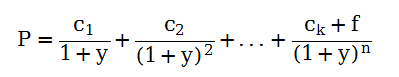
四、统计分布

统计学中有很多的统计分布，正态分布、对数正太分布、分布，t分布、f分布、稳态分布、极值分布等等。在这里我们就简单写几个，实际上网上介绍的更为全面。

1、正态分布

这个是最理论化、最常用的一种统计分布，在金融中经常假设资产收益率服从正态分布，原因是正态分布具有良好的统计特征。但是实际上，理论与实际是有很大差距的。

（1）简单收益率的定义是:(收益/投入资金)×100%。根据这个定义,简单收益率的取值范围是[-100%,+∞)。它不可能小于-100%,因为投入资金不可能是负值。而正态分布是一种概率分布,它的取值范围是(-∞,+∞)。正态分布没有基于投入资金这一先验条件,所以其值可以为任意正值或负值。标准正常分布的密度曲线呈钟形,大部分值聚集在平均值附近,但理论上可以取任意值。

所以,简单收益率和正态分布的主要差异在于:

①. 简单收益率有着>-100%的理论下限,它基于投入资金这一先验条件。而正态分布作为一般概率分布不存在此限制,其值域是开区间。

②. 简单收益率的可能值会更加集中在中心,正态分布的可能值则呈均匀分布在整个值域内。简单收益率不太可能达到极值,而正态分布则有一定概率达到离均值很远的极值。

③. 简单收益率的分布更加偏态,正态分布的分布则是对称的钟形曲线。

④. 简单收益率的期望值一般大于0,而正态分布的期望值可以是任意实数。

（2）多期毛收益率是单期毛收益率的乘积，不再服从正态分布。

假设每个期间的单期毛收益率是独立同分布的随机变量，且服从正态分布。在这种情况下，单期收益率的乘积就会导致多期收益率的分布发生变化。乘积的结果会受到累积效应的影响，即多期的波动性可能会更大。

具体来说，当乘积的因子超过1时，每个因子的正态分布的均值影响乘积的增长，从而导致多期收益率的分布偏向正偏态（右偏）。而当乘积的因子小于1时，每个因子的正态分布的均值影响乘积的减小，从而导致多期收益率的分布偏向负偏态（左偏）。

因此，多期毛收益率的分布通常会偏离正态分布，并且会展现出更大的尾部风险（fat-tail risk）。这意味着在投资决策和风险管理中，我们需要考虑更多因素，例如波动性的增加、非线性关系的影响以及可能的极端事件。

在实践中，为了更准确地描述多期收益率的分布特征，常常采用其他分布模型，如对数正态分布、广义正态分布等，来更好地捕捉尾部风险和非正态特征。这有助于更精确地评估投资策略的风险和收益特征。

（3）收益率分布大多是厚尾的，不符合正态分布的尾部特征。

正态分布是一个典型的薄尾分布,它的尾部衰减很快。例如,在标准正态分布中,x=3处的密度只有x=0处的密度的0.003%,x=4处的密度已减小到0.000032%。这意味着正态分布很难产生3个标准差以外的极端值。但收益率分布的尾部通常比正态分布更加"厚",极端值更易发生。这是因为:

①、收益率随着时间的增长呈现出累乘效应,会放大positive和negative值之间的差距,产生更大范围的值。这与正态分布的值是各期加总不同。

②. 收益率分布受到极端事件影响更大,如突发事件、金融危机等,这会增加其尾部值。而正态分布作为一般概率分布不包含此类专有影响。

③. 收益率的值域受到下限的约束更小,如-100%。这意味着更大的概率会集中在中心类值,但不排除更大正值的出现,导致右尾更厚。

④. 收益率分布往往会更加偏态,右尾往往比左尾更长和更厚,这也与正态分布的对称分布不同。因此,收益率分布的尾部通常比正态分布更加厚长,具有更高的偏度,更易产生极端值。这使得我们难以用正态分布模型来很好地拟合和评估收益率分布。我们需要建立新的厚尾分布模型,如学生t分布、幂律分布、Extreme Value分布等来提高拟合效果。

2、对数正态分布

对数正态分布指一个随机变量的对数服从正态分布，则该随机变量服从对数正态分布，设x为正的连续随机变量，其概率密度为：

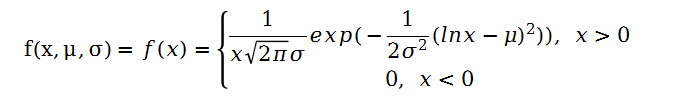
则称随机变量x服从对数正态分布，记为lnx~N(μ，σ2)

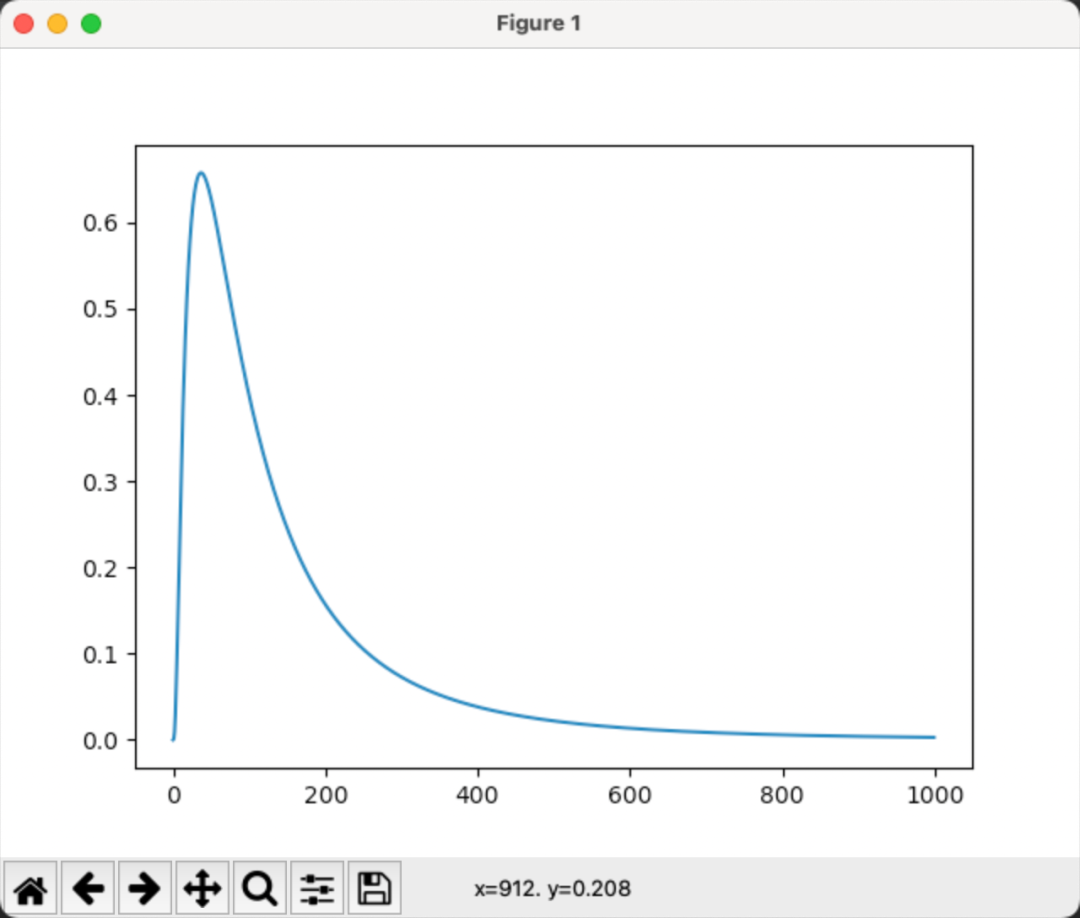
代码详见：

import pandas as pd
import numpy as np
from scipy.stats import lognorm
from scipy import stats
import matplotlib.pyplot as plt

# 输出从0-10，步长为0.01
x = np.arange(0, 10, 0.01)
# 使用lognorm.pdf 画出对数正态分布概率密度图
y = pd.Series(stats.lognorm.pdf(x, 1, 0, 1))
# 画出y
y.plot()
# 显示图形
plt.show()

在金融计量分析中，如果对数收益率独立服从正态分布N(),则简单收益率服从对数正态分布。推导如下：

如果对数收益率y=ln(x)独立服从正态分布N(μ,σ^2),即:y ~ N(μ, σ^2)则原始的简单收益率x将服从对数正态分布,其概率密度函数为:f(x;μ,σ^2) = (1/xσ√2π)exp{-(ln x - μ)^2 / 2σ^2}这是因为对数和指数运算可以使随机变量的分布发生变换。

具体证明如下:

• ①. 令z=ln x,则有x=exp(z),那么x的概率密度函数为:f(x) = f(exp(z)) = (d/dx)f(exp(z))|exp'(z)|= f(z)exp'(z) = f(z)exp(z)其中f(z)为z的概率密度函数。

• ②. 因为z ~ N(μ, σ^2),则f(z)为正态分布概率密度函数:f(z) = (1/√2πσ^2)exp{- (z - μ)2 / 2σ^2}

• ③. 代入上一步中的f(x),得到:f(x) = (1/√2πσ^2)exp{- (z - μ)2 / 2σ^2} x =(1/xσ√2π)exp{-(ln x - μ)^2 / 2σ^2}这就是对数正态分布的概率密度函数表达形式。

实际上大部分股票的收益率特征还是不符合对数正态分布。当然，还有很多其他分布，例如：稳态分布、极值分布等，

因为这块过于学术，而且具体深入讨论起来，还可以水1-2篇，所以为了这个系列整体性、学术与实操兼容性，这块不做深入研究和赘述了。并且在大纲中基础内容第一篇还有收益率分布特征我们给予删除，新增上述内容的一个实操。

五、本节实操案例

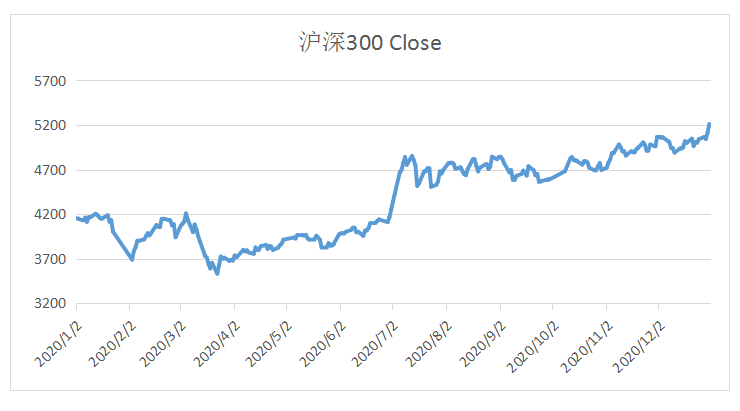
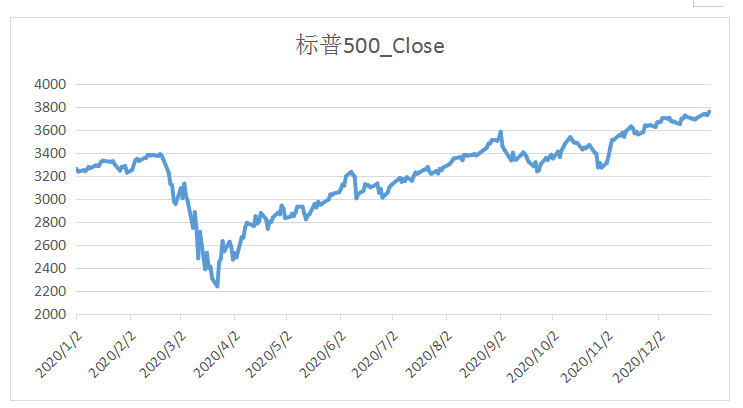
2020年疫情期间中美股市对比

接下来我们进行基本的描述性定性统计分析，如下表所示：

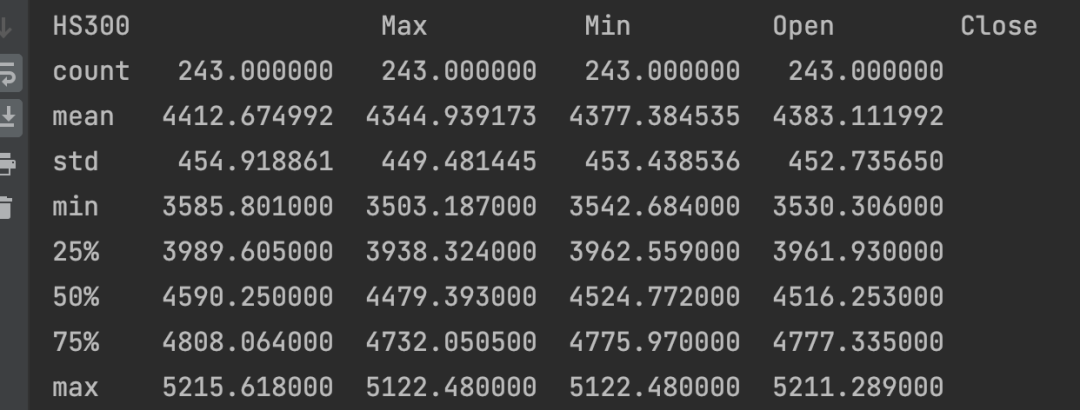
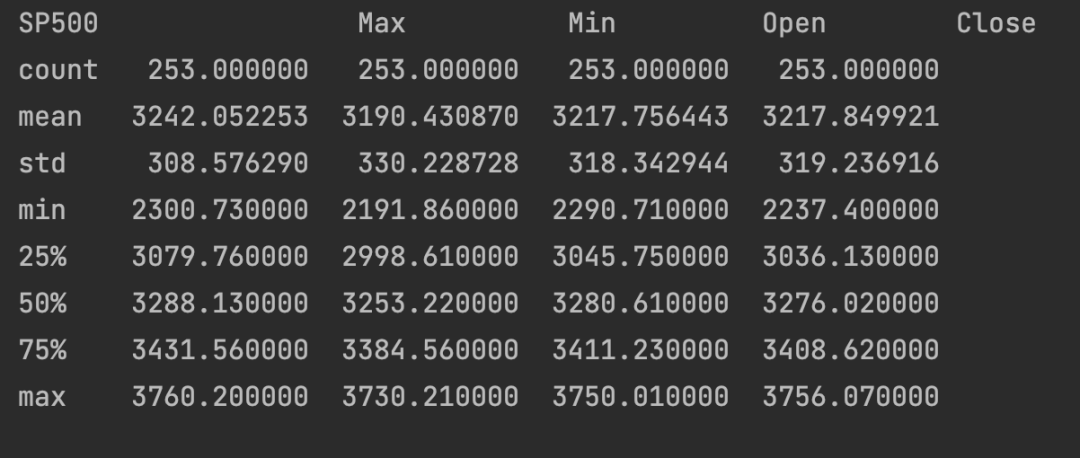
接下来，我们计算沪深300与标普500的简单收益率和对数收益率，如下图所示：

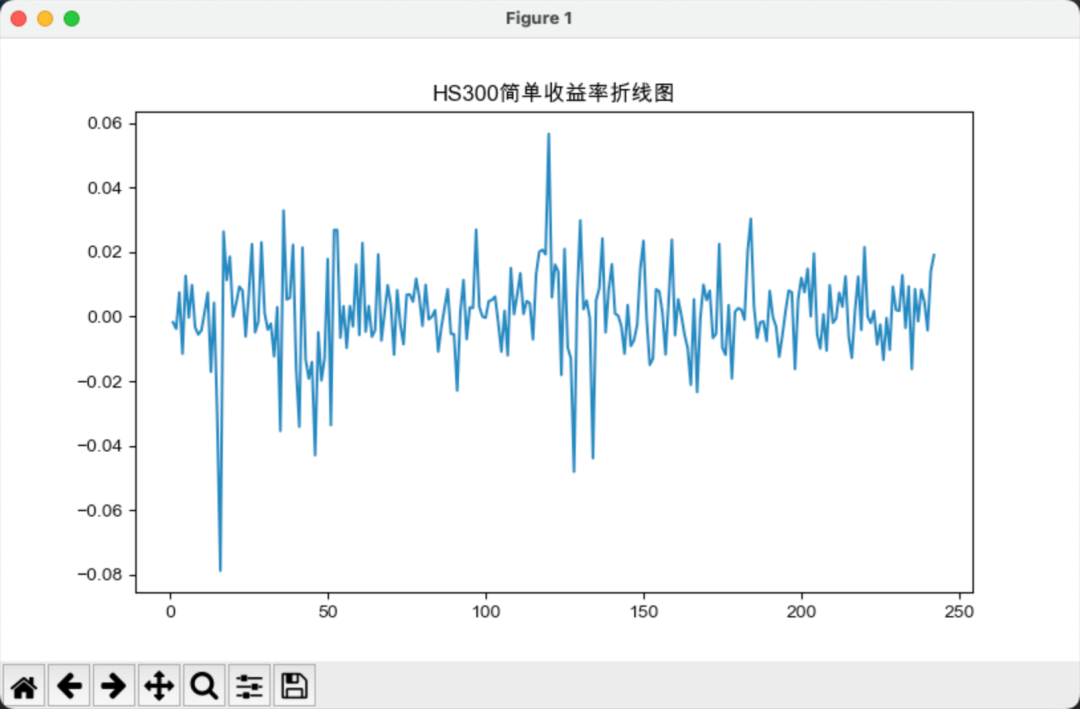
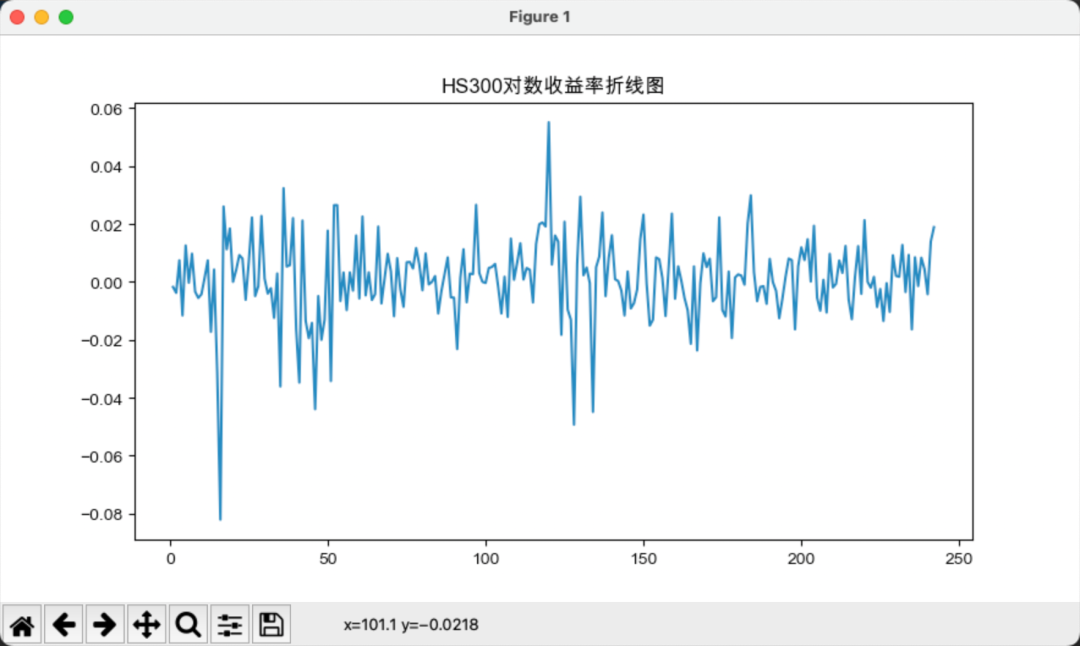
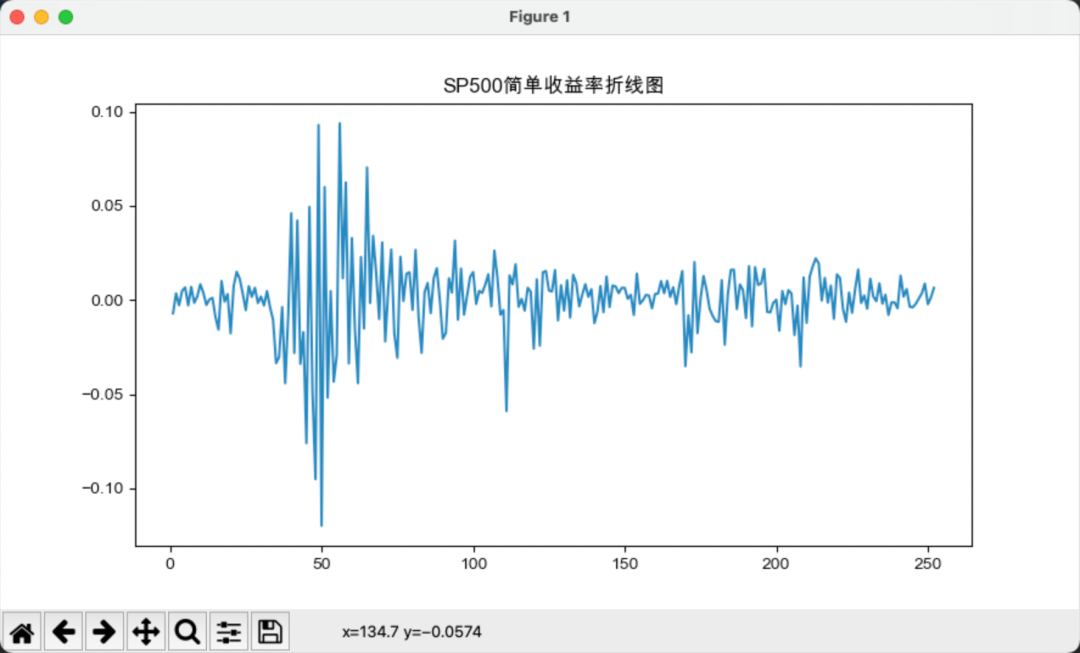
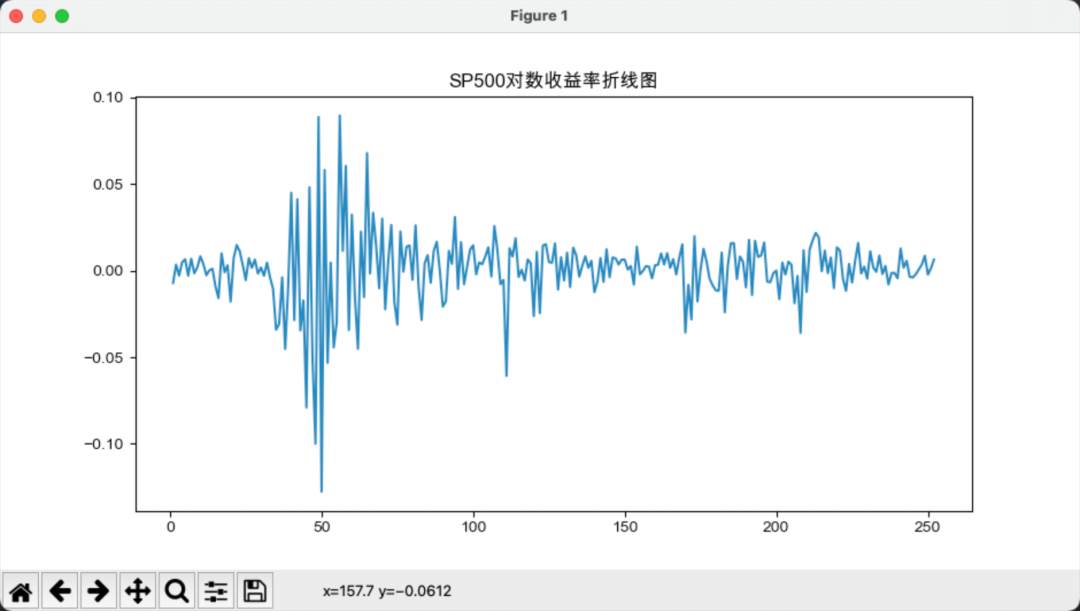
相对而言，简单收益率的波动要大于对数收益率的波动。

现在分析中美指数的对数收益率的波动率，对数收益率的波动率可通过下式计算：

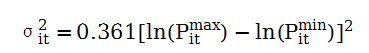
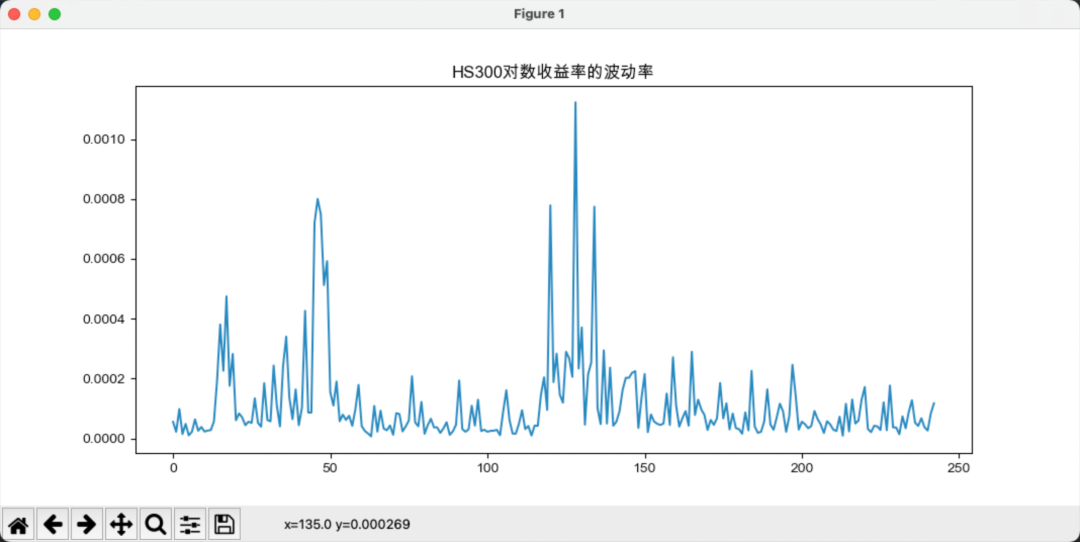
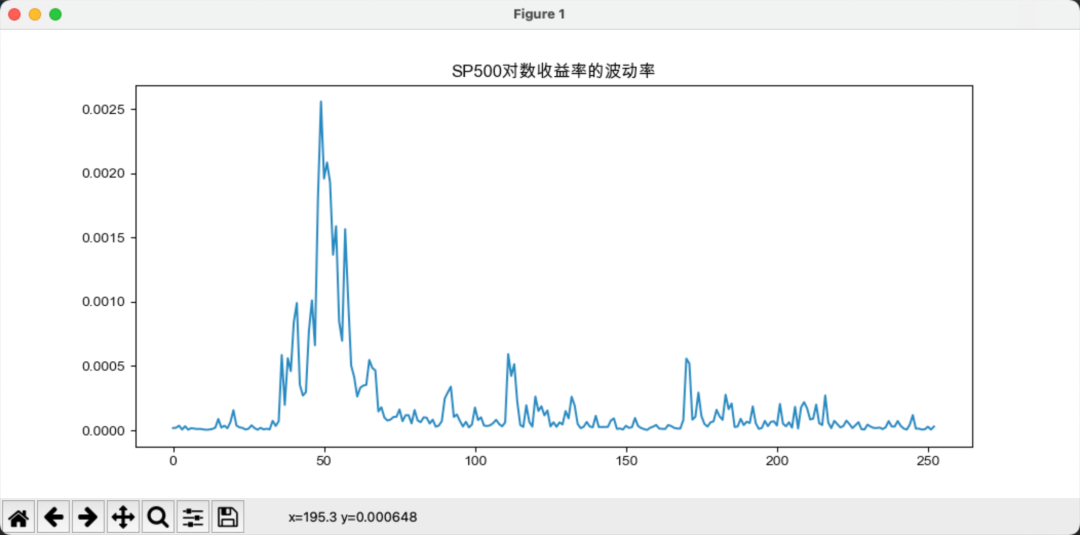
上图中可以清楚看到，在2020年初和2020年中，中国股指波动率出现了一个显著的上升，而美国在2020年初出现了巨大的波动。

代码如下：

# 计算对数收益率的波动率
sigma2 = 0.361*(np.log(df['Max']) - np.log(df['Min']))**2

在对收益率的研究中，我们既可以选择研究简单收益率，也可以选择研究对数收益率。我们对金融时间序列的分布性质进行检验并估计密度函数，首先来看直方图，如下图所示：

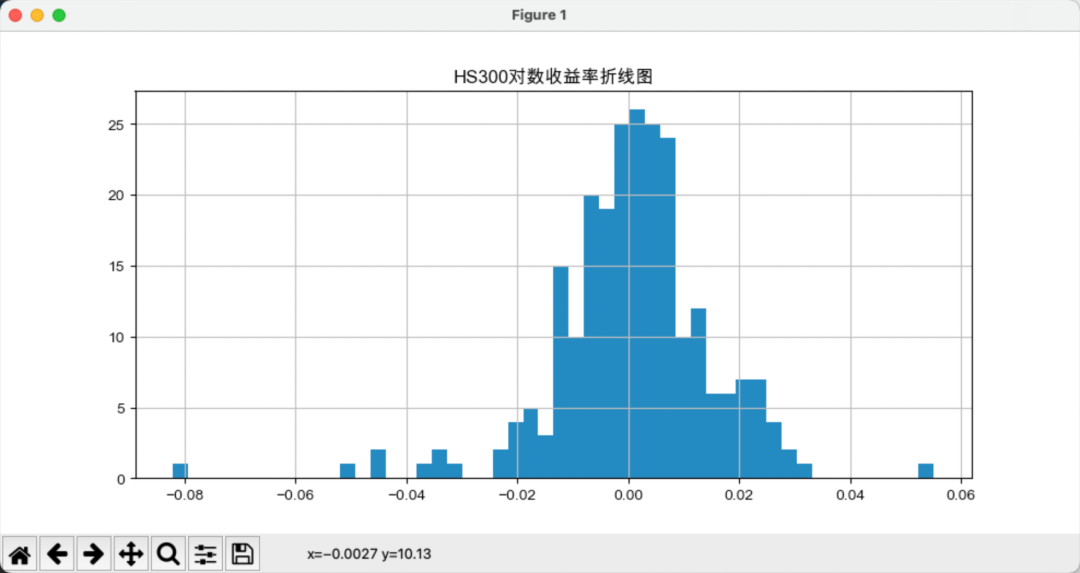
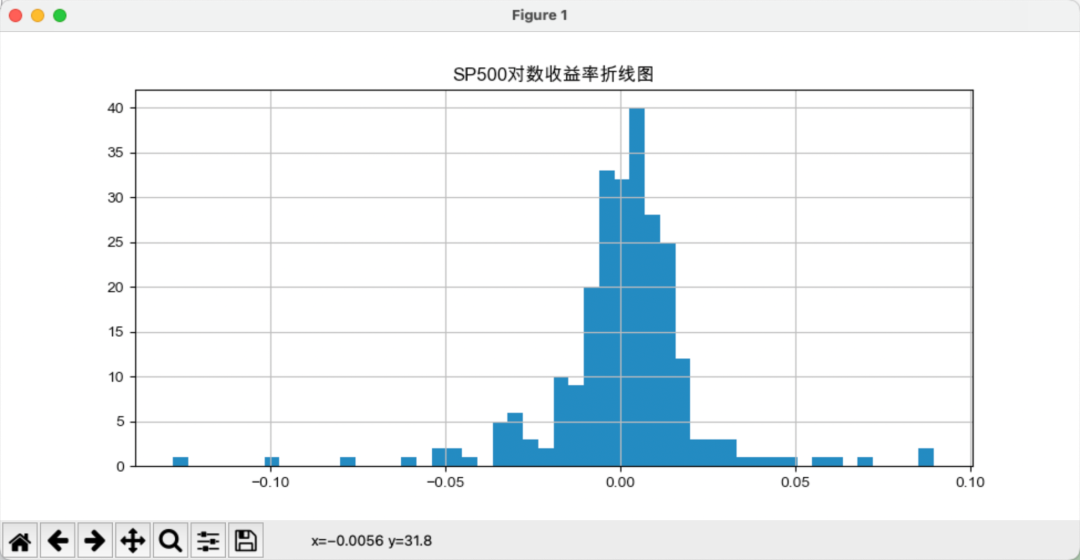
从形状来看，对数收益率分布类似正态分布，直方图是分布密度的一个比较粗糙的估计量。上图也可以看出，标普500比指数的峰度更大，说明投资风险更高，峰度(Kurtosis)是用于衡量概率分布尾部厚度的统计量。

峰度更大表明分布具有更厚的尾部和更高的偏度,意味着极端值更为频繁,从而风险更高。

代码如下：

对数收益率的直方图

# df['log_return'].hist(bins=50)
# # df['log_return'].plot()
# plt.title(f'{file}对

下面对数据进行正态分布检验，qq图是正态分布检验最常用且最直观的方法。

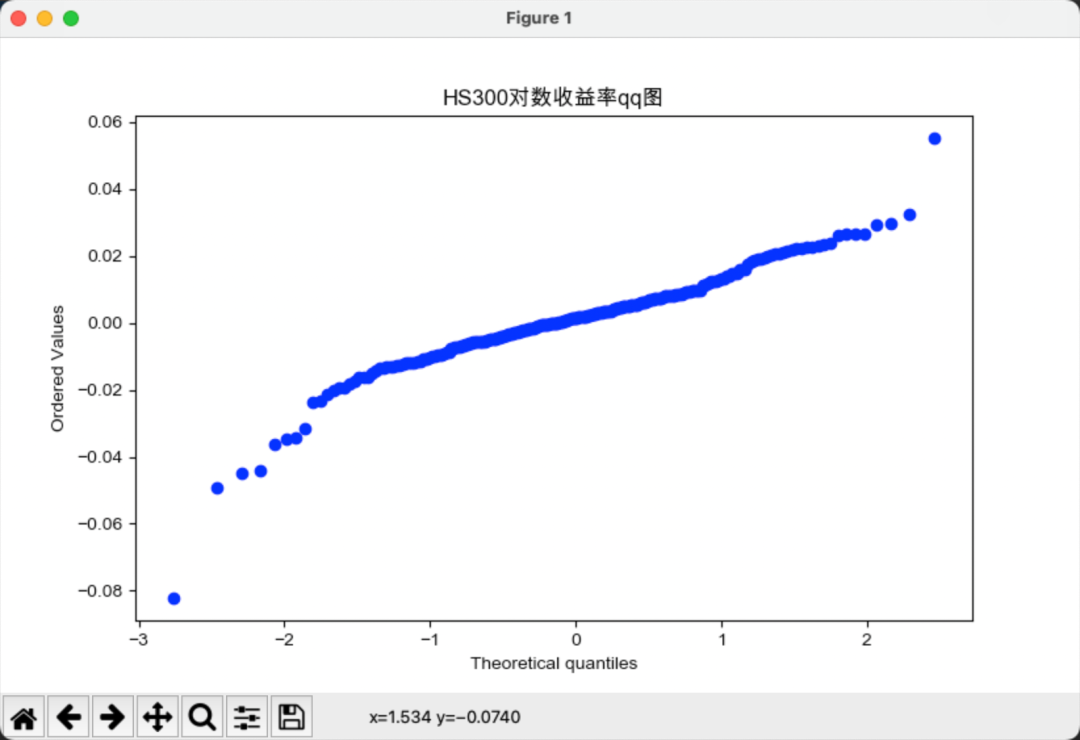
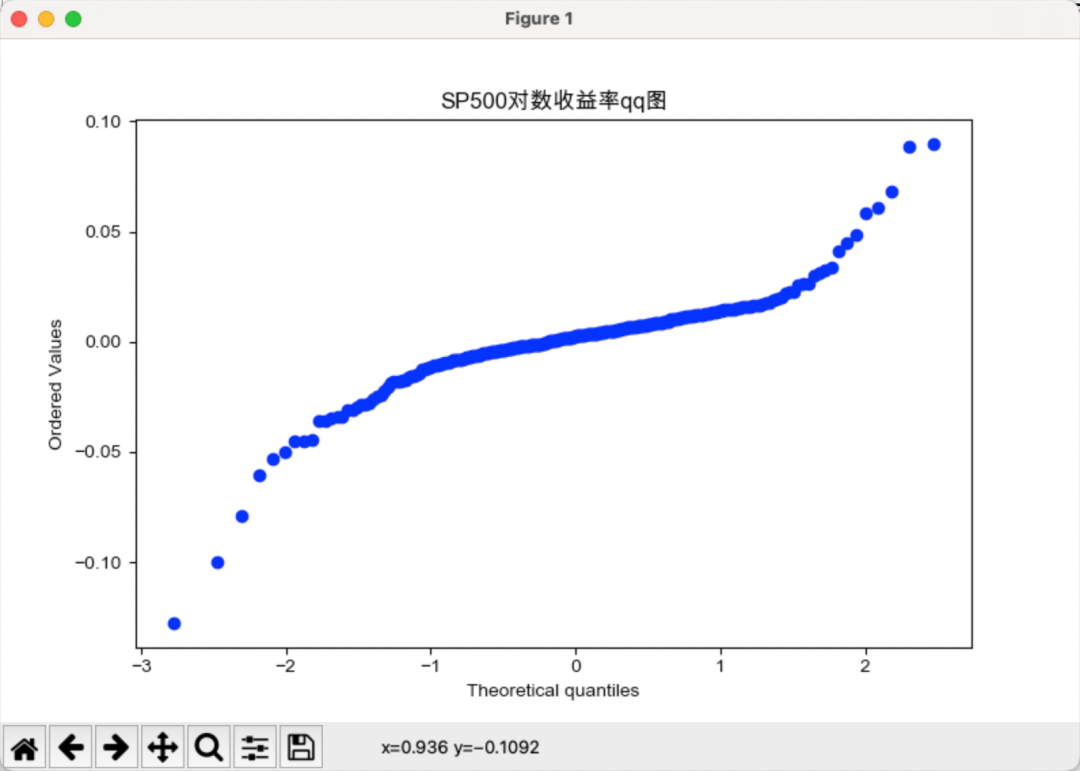
通过qq图我们可以看到，分为数并不能很好的拟合，由此可以初步判断，沪深300和标普500指数的对数收益率不服从正态分布。且可以看出，标普500的尾部极端风险更大。

代码如下：

# 画对数收益率的qq图
# stats.probplot(df['log_return'], dist='norm', plot=plt)
# plt.title(f'{file}对数收益率qq图')

下面进行Shapiro-Wilk检验，Shapiro-Wilk检验作为正态性检验的重要方法之一,主要适用于小样本(3 < n < 5000)的情况。它可以判断我们的样本是否符合正态分布,为我们推断统计应用中的许多假设提供支持。但其检验力较差,仅当样本违反正态性较为明显时才可能判断为不来自正态分布。

HS300的shapiro-wilk检验结果= ShapiroResult(statistic=0.9280851483345032, pvalue=1.8255343903206267e-09)

SP500的shapiro-wilk检验结果= ShapiroResult(statistic=0.8459327220916748, pvalue=4.009484242420381e-15)

两者的p值都很小，说明拒绝了原假设，从而两者分布均不服从正态分布。

代码如下：

# 进行shapiro-wilk检验
print(f'{file}的shapiro-wilk检验结果=', stats.shapiro(df['log_return'].dropna()))

总结

上述内容就是我们金融计量经济学第1节内容了，后面按照大纲内容我们会按部就班的更新，争取一周一更。

具体代码和数据大家可以公众号回复：计量01。

任何问题大家也可以加入松鼠会员群，群里有股票、期货、数字货币各个行业大佬，无论你是求职、学习、还是亏的受不了了，我相信量化可能不会让你一夜翻身，但是绝对会让你活的更长，认知更深，只要活下来，就有机会翻身农奴把歌唱。