写在前面的话

书上学来终觉浅，绝知此事要躬行。

回顾

1、与$k$-Anonymity不同，差分隐私是算法的属性，而不是数据的属性。也就是说，我们可以证明算法满足差分隐私。

2、随机函数$F$中的随机性应该是"足够的"，以便从$F$观察到的输出不会揭示$x$或$x^{\prime }$中哪一个是输入。

3、当$ϵ$越小时，数据效用越低，隐私保护程度越高；当$ϵ$越大时，数据效用越高，隐私保护程度越低。

4、普遍的共识是$ϵ$应该在1左右或更小，并且$ϵ$的值高于10可能对保护隐私没有多大作用 ，但这个经验法则可能会变得非常保守。

5、拉普拉斯机制不会拒绝被确定为恶意的查询，相反，它增加了足够的噪音，恶意查询的结果对对手毫无用处。

讲完了拉普拉斯，我们来看看差分隐私的组合定理~

差分隐私的属性（Properties of Differential Privacy）

由差分隐私的定义，所产生的差分私有机制的三个重要属性。

这些属性将帮助我们设计满足差分隐私的有用算法，并确保这些算法提供准确的答案。

这三个属性是：

1、顺序组成（Sequential composition）

2、平行组合（Parallel composition）

3、后处理（Post processing）

顺序组成（Sequential composition）

差分隐私的第一个主要性质是顺序组合，它限制了在同一输入数据上发布多个差私有机制结果的总隐私成本。

形式上，差分隐私的顺序组合定理说：

如果$F_1(x)$满足${ϵ}_1$-差异隐私

并且$F_2(x)$满足${ϵ}_2$-差分隐私

则释放两个结果的机制$G(x)=(F_1(x),F_2(x))$满足${ϵ}_1+{ϵ}_2$-差分隐私。

顺序组合是差分隐私的重要属性，因为它可以设计出多次查阅数据的算法。

当对单个数据集执行多个单独的分析时，顺序组合也很重要。

因为它允许个人通过参与所有这些分析来约束他们产生的总隐私成本。

顺序组合给出的隐私成本的界限是一个上限，两个特定的差异隐私机制的实际隐私成本可能小于此，但永远不会比这个更大。

如果我们检查来自一个将两个差分隐私结果平均在一起的机制的输出分布，那么$ϵ$的"相加"原则是有意义的。

上例子！

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
epsilon1 = 1
epsilon2 = 1
epsilon_total = 2

# satisfies 1-differential privacy
def F1():
    return np.random.laplace(loc=0, scale=1/epsilon1)

# satisfies 1-differential privacy
def F2():
    return np.random.laplace(loc=0, scale=1/epsilon2)

# satisfies 2-differential privacy
def F3():
    return np.random.laplace(loc=0, scale=1/epsilon_total)

# satisfies 2-differential privacy, by sequential composition
def F_combined():
    return (F1() + F2()) / 2

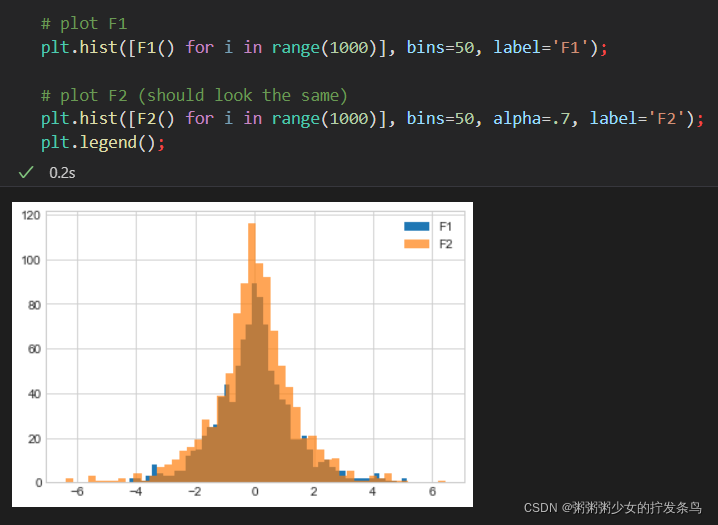
如果我们绘制F1 和 F2 ，我们会看到它们的输出的分布看起来非常相似。

# plot F1
plt.hist([F1() for i in range(1000)], bins=50, label='F1');

# plot F2 (should look the same)
plt.hist([F2() for i in range(1000)], bins=50, alpha=.7, label='F2');
plt.legend();

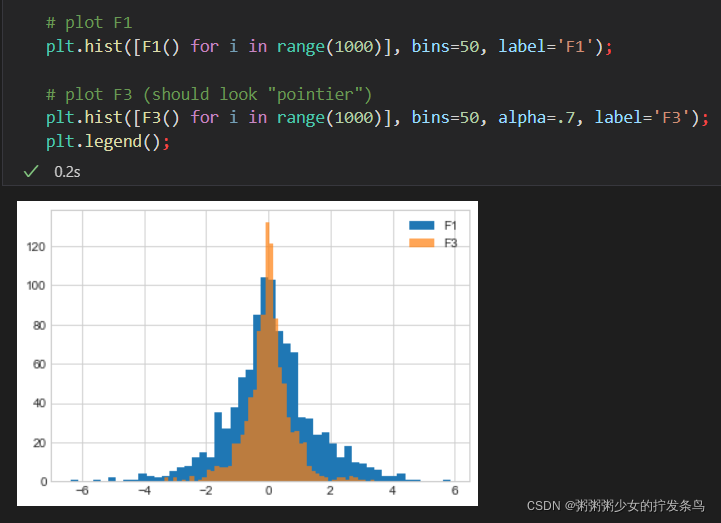
如果我们绘制F1 和F3 ，我们看到输出的分布看起来F3比F1的分布**“更尖锐更瘦窄”**。

# plot F1
plt.hist([F1() for i in range(1000)], bins=50, label='F1');

# plot F3 (should look "pointier")
plt.hist([F3() for i in range(1000)], bins=50, alpha=.7, label='F3');
plt.legend();

因为它的$ϵ$越高，意味着隐私性越低，因此获得的结果与真实答案越相近。

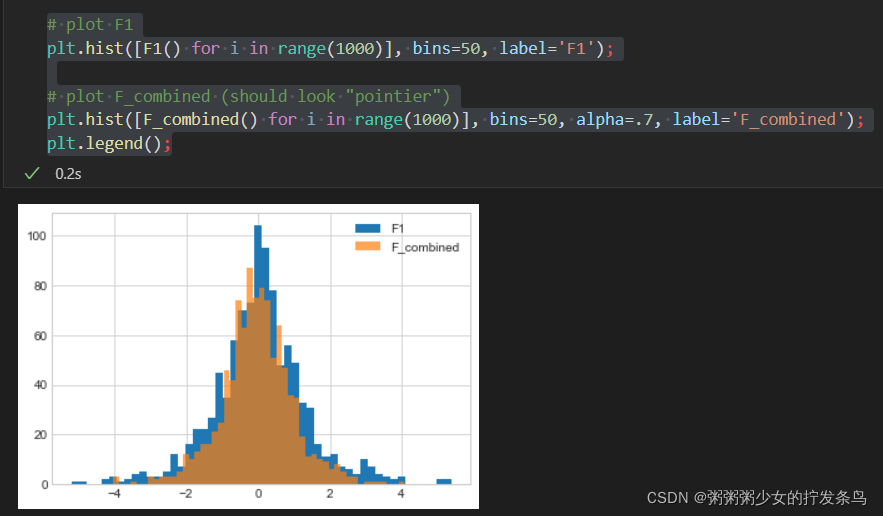
如果我们绘制F1 和F_combined ，我们会看到输出F_combined的分布较于F1"更尖锐更瘦窄"。

# plot F1
plt.hist([F1() for i in range(1000)], bins=50, label='F1');

# plot F_combined (should look "pointier")
plt.hist([F_combined() for i in range(1000)], bins=50, alpha=.7, label='F_combined');
plt.legend();

这意味着它的答案比F1的答案更准确。

虽然只是做了一个平均的操作，但是结果告诉我们它的$ϵ$必须更高（即它产生的隐私比 ） 要高。

那么F3 和F_combined呢？回想一下，这两种机制的$ϵ$值是相同的 - 两者的$ϵ$均为 2。它们的输出分布应该看起来相同。

# plot F3
plt.hist([F3() for i in range(1000)], bins=50, label='F3');

# plot F_combined (should look "pointier")
plt.hist([F_combined() for i in range(1000)], bins=50, alpha=.7, label='F_combined');
plt.legend();

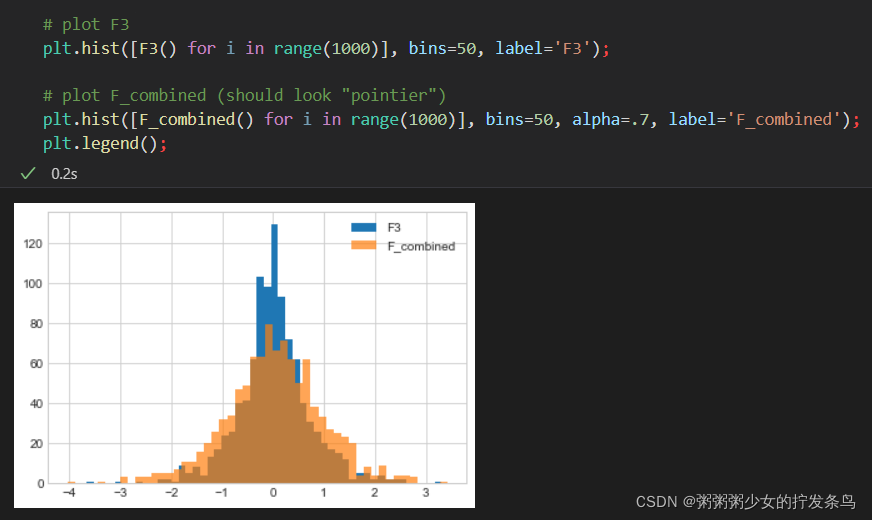
事实上，F3看起来"更尖锐更瘦窄"！为什么会发生这种情况？

请记住，顺序组合在几个版本的总$ϵ$上的上限，但是实际上对隐私的实际累积影响可能较低，并不与总$ϵ$上的上限效果一致。

在这种情况下，实际的隐私损失似乎略低于由顺序组合确定的上限$ϵ$。

总的来说顺序组合是控制总隐私成本的一种非常有用的方法，我们将看到它以许多不同的方式使用，但请记住，它不一定是一个确切的边界。

平行组合（Parallel Composition）

差分隐私的第二个重要性质称为并行组合。

并行组合可以看作是顺序组合的替代方案，第二种计算多个数据发布的总隐私成本边界的方法。

并行组合基于将数据集拆分为不相交的块，并在每个块上单独运行差异私有机制的想法。

由于块是不相交的，因此每个个体的数据只出现在一个块中 。因此，即使总共有$k$块，该机制也会对每个个体的数据运行一次。

正式一点说：

如果$F(x)$满足$ϵ$-差分隐私，我们将数据集$X$拆分为$k$不相交的块，使得$x_1\cup ...\cup x_k=X$

然后，释放所有结果的机制$F(x_1),...,F(x_k)$满足$ϵ$-差分隐私

这是一个比顺序组合更好的绑定。由于我们运行$F$ $k$次，顺序组合会说此过程满足$kϵ$-差分隐私。

并行组合允许我们说总隐私成本只是$ϵ$。

正式定义与我们的直觉相匹配，如果数据集中的每个参与者都向$X$贡献了一行，则此行将恰好出现在块之一$x_1,...,x_k$中。这意味着$F$只会"看到"这个参与者的数据一次，这意味着$ϵ$的隐私成本适合该个人。由于此属性适用于所有个人，因此每个人的隐私成本为$ϵ$。

直方图（Histograms）

在我们的上下文中，直方图是对数据集的分析，该数据集根据其中一个数据属性的值将数据集拆分为"条柱"，并计算每个条柱中的行数。

例如，直方图可能会计算数据集中达到特定教育水平的人数。

adult = pd.read_csv("adult_with_pii.csv")
adult['Education'].value_counts().to_frame().head(5)

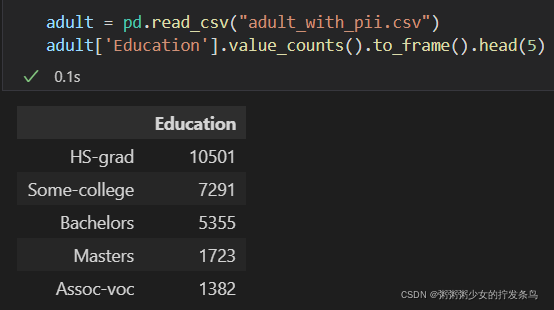
直方图对于差分隐私特别有趣，因为它们会自动满足并行组合。

直方图中的每个"条柱"都由数据属性的可能值定义（例如，'Education' == 'HS-grad'）。

单个行不可能同时具有属性的两个值，因此以这种方式定义条柱可以保证它们不相交。

因此，我们已经满足了并行组合的要求，并且我们可以使用差分私有机制来释放所有"条柱"计数，总隐私成本仅为$ϵ$。

epsilon = 1

# This analysis has a total privacy cost of epsilon = 1, even though we release many results!
f = lambda x: x + np.random.laplace(loc=0, scale=1/epsilon)
s = adult['Education'].value_counts().apply(f)
s.to_frame().head(5)

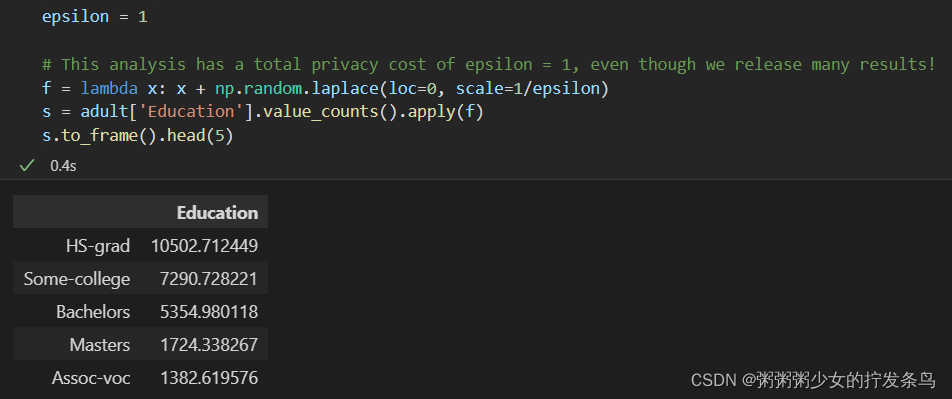
列联表（Contingency Tables）

列联表或交叉制表（通常缩写为交叉表）就像一个多维直方图。

它计算数据集中具有特定值的行的频率，这些行一次具有多个属性。

在分析数据时，列联表经常用于显示两个变量之间的关系。

例如，我们可能希望查看基于教育水平和性别的计数：
关于pandas中crosstab的用法

pd.crosstab(adult['Education'], adult['Sex']).head(5)

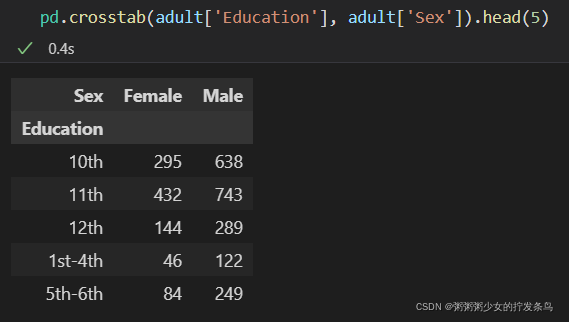
就像我们之前看到的直方图一样，数据集中的每个人都只参与此表中出现的一个计数。

对于在构建列联表时考虑的任何一组数据属性，任何单个行都不可能同时具有多个值。

因此，在这里使用并行组合也是安全的。
python中的apply(),applymap(),map() 的用法和区别

ct = pd.crosstab(adult['Education'], adult['Sex'])
f = lambda x: x + np.random.laplace(loc=0, scale=1/epsilon)
ct.applymap(f).head(5)

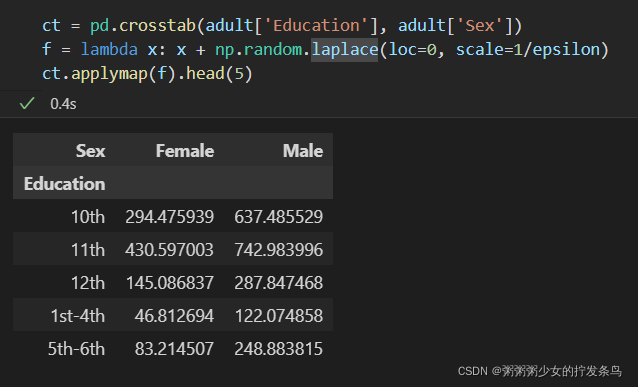
还可以生成包含 2 个以上变量的列联表。但是，请考虑每次添加变量时会发生什么：每个计数都倾向于变小。

直观地说，当我们将数据集拆分为更多块时，每个块中的行数都会减少，因此所有计数都会变小。

这些缩小的计数会对我们从中计算出的差分隐私结果的准确性产生重大影响。

如果我们从信号和噪声的角度来考虑事物，那么大量的计数代表一个强信号，它不太可能被相对较弱的噪声（就像我们上面添加的噪声）干扰太多，因此即使在添加噪声之后，结果也可能是有用的。

然而，一小段计数代表一个微弱的信号，可能与噪声本身一样弱，并且在我们添加噪声后，我们将无法从结果中推断出任何有用的东西。

因此，虽然并行组合似乎为我们提供了"免费"的东西（以相同的隐私成本获得更多结果），但事实并非如此。

并行组合只是沿着不同的轴移动准确性和隐私之间的权衡，当我们将数据集拆分为更多块并发布更多结果时，每个结果都包含较弱的信号，因此准确性较低。

后处理（Post-processing）

这个想法很简单：通过以某种方式对数据进行后处理，不可能逆转差异隐私提供的隐私保护。

正式一点说：

如果$F(X)$满足$ϵ$-差分隐私，则对于任何（确定性或随机化）函数$g$, $g(F(X))$满足$ϵ$-差分隐私。

后处理属性意味着对差分私有机制的输出执行任意计算始终是安全的，不存在逆转该机制提供的隐私保护的危险。

特别是，可以执行后处理，这可能会减少噪声或改善机制输出中的信号。

例如，对于不应返回负结果的查询，将负结果替换为零。之前在差分隐私群里看到一个小伙伴弄电影评分的差分隐私，说是出现负数怎么办。就是利用后处理设为0就好，结果还是满足差分隐私的。

事实上，许多复杂的差分私有算法利用后处理来减少噪声并提高结果的准确性。

后处理属性的另一个含义是，差分隐私提供了对基于辅助信息的隐私攻击的抵抗力。

例如，函数$g$可能包含有关数据集元素的辅助信息，并尝试使用此信息执行链接攻击。

后处理属性表示，无论$g$中包含的辅助信息如何，此类攻击的有效性都受到隐私参数$ϵ$的限制。

总结

1、顺序组合给出的隐私成本的界限是一个上限，两个特定的差异隐私机制的实际隐私成本可能小于此，但永远不会比这个更大。

2、实际的隐私损失似乎略低于由顺序组合确定的上限$ϵ$。

3、如果数据集中的每个参与者都向$X$贡献了一行，则此行将恰好出现在块之一$x_1,...,x_k$中。这意味着$F$只会"看到"这个参与者的数据一次，这意味着$ϵ$的隐私成本适合该个人。由于此属性适用于所有个人，因此每个人的隐私成本为$ϵ$。

4、单个行不可能同时具有属性的两个值，因此以这种方式定义直方图中条柱可以保证它们不相交。

5、对于在构建列联表时考虑的任何一组数据属性，任何单个行都不可能同时具有多个值。因此，在这里使用并行组合也是安全的。

6、执行后处理，这可能会减少噪声或改善机制输出中的信号。