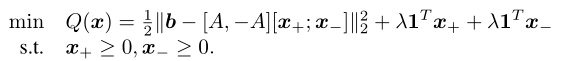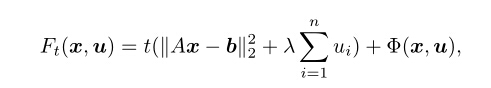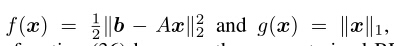1：解决的问题模型如下：

 
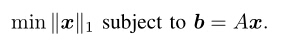
或者约束条件可以适当的松弛，即为如下模型：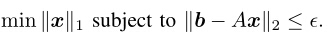 
 
当然约束条件取l2l2范数，bb数据获取的比较准确，结果逼近的效果更好，防止过拟合。如果取l1l1 范数，则是获取的bb数据，受到污染比较严重。并且bb 本身就是稀疏的。这也是人的经验对于模型的成功也是很重要的。 
2：几类优化算法 
(1)梯度投影算法Gradient Projection Methods 
原问题可以变为如下问题：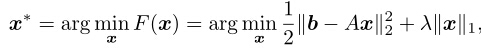 
 
下面介绍两种方法对其进行处理。 
i)上式又等价于： 

 
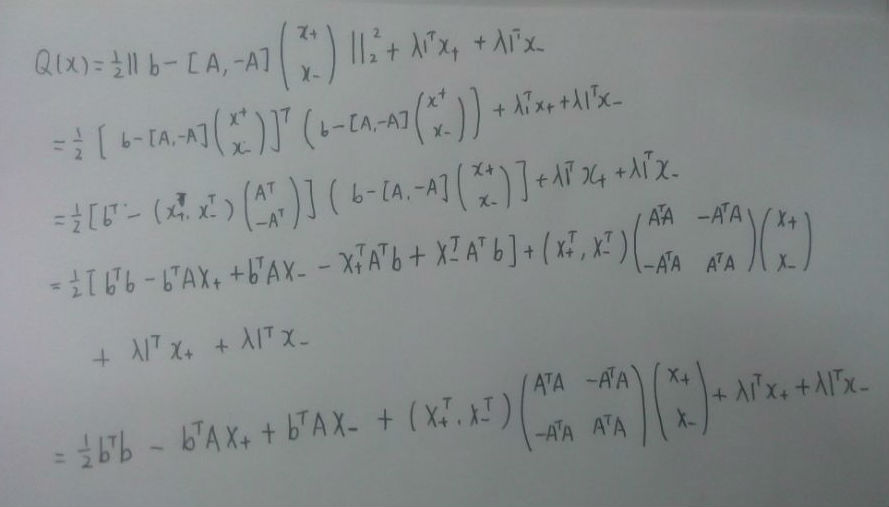
所以就有如下记号和约定：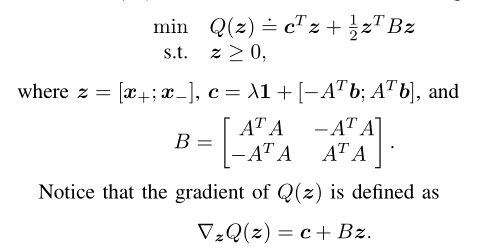 
 
更新zkzk 时沿着负梯度的方向下降最快。但是只是局部最小值。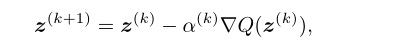 
 
其中akak 是步长，可以用线搜索的方法来确定最优步长。 
下介绍第二种方法 truncated Newton interior-point method. 
ii)上式又等价于：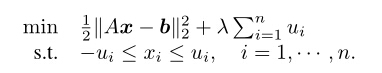 
 
利用内点法的把约束条件给罚到目标函数上去。 
在这里我们对约束条件利用logarithmic barrier函数进行改写。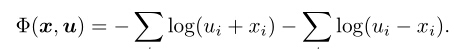 
 
在这里，我们可以看到当xixi 越接近ui或者−uiui或者−ui的时候，函数值会变得越大。当xixi 无限趋近于ui或者−uiui或者−ui时，则函数值无限趋于无穷大。所以只有当xixi 趋近于0时候，函数值才趋近于一个常数。 
所以上式可以等价于如下模型： 

然后利用牛顿算法进行求解计算。

(2)迭代阈值收缩算法 Iterative Shrinkage-Thresholding Methods 
对于一般的模型：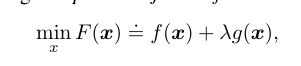 
 
其中：

对f(x)f(x) 二次近似。则问题转变成如下：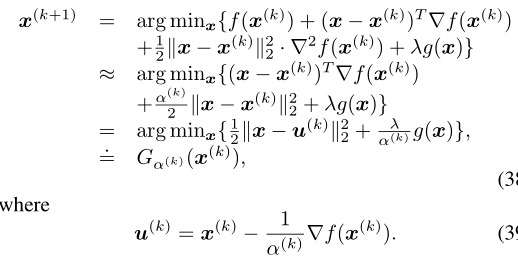 
 
可以适用迭代阈值算法。关于l_{1}范数最优化的迭代阈值算法的证明可以参见我的另一篇博客

(3)近端梯度算法 Proximal gradient method 
其处理的模型如下：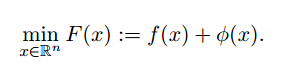 
 
其中f(x)f(x)是连续可微的，微分函数满足利普希茨条件成立：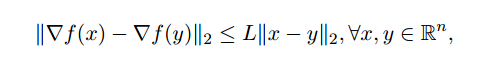 
 
其中LL相当于代替f(x)f(x)的二阶偏导。 
那么可以进行如下算法来解决问题：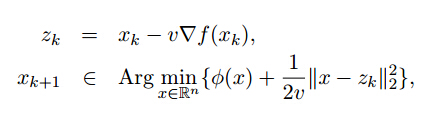 
 
说明： 
第一步的更新：按照f(x)f(x)沿着负梯度的方向下降最快 
第二步的更新：有数值解，进行软阈值操作。 
(4)交替方向法 Alternating Direction Methods 
其实利用的是拉格朗日算法，来进行更新出来。解决的模型如下：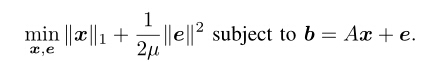 
 
其拉格朗日函数如下：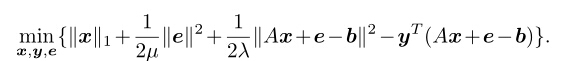 
 
问题变为分别最小化x,e,yx,e,y。 
说明： 
更新ee时，固定x,yx,y，直接求导，ee有数值解。 
更新xx 时，固定e,ye,y经过化简，可以运用软阈值进行操作计算。 
更新yy时，固定x,ex,e，直接求导，yy有数值解。

Fast ℓ 1-minimization algorithms and an application in robust face recognition