案例1 生产决策问题 (一个简单的线性规划问题)
某工厂在计划期内要安排I、II两种产品生产。生产单位产品所需的设备台时,A,B两种原材料的消耗,资源的限制以及单件产品利润如下表所示

问工厂应分别生产多少单位产品I和产品II,才能获利最多?
【问题分析】
- 这是一个生产决策问题,决策者的目标是生产利润最大
- 与利润有关的是产品的销售量与售价(或单位利润)
- 生产产品就要消耗资源(这与产量有关),而各种资源又受到数量限制。
经验:收入与销售量有关,而资源的消耗量与产品的产量有关。
【问题假设】
- 产品I的产量等于销售量;
- 产品II的产量等于销售量。
【符号设置】
- x1 产品I的一个周期的产量 (单位:件);
- x2 产品II的一个周期的产量 (单位:件);
- z 工厂一个周期内的总利润 (单位:元)。
(其中,x1, x2 称为决策变量,决策者唯一能自己决定取值的变量。)
【建立模型】
工厂一个生产周期的总利润 : ![]()
生产资料约束:
| 资源的实际消耗 | 限制 | 资源的拥有量 | |
| 设备限时 | x1 +x2 | <= | 300 |
| 原料A限量 | 2x1+x2 | <= | 400 |
| 原料B限量 | x2 | <= | 500 |
其它约束:
因为x1和x2都是产品的产量,所以,从数学意义上,有![]()
厂家的诉求:
一个周期内利润 z 越大越好!(max z)
以上分析,将生产过程的未知要素(产品产量)用x1, x2表示,各种客观约束都表达为x1,x2的函数不等式,厂家的诉求(利润)也是x1,x2的函数表达式,将这些数学式子写在一起,就是这个规划问题的数学模型.
【数学模型】

这个规划模型,如果抛开这个问题的背景,就是求在五个约束条件下,二元一次函数z=50x1+100x2的最大值,这是一个纯数学意义上的极大值问题。

虽然有些问题的数学结构很难用数学式子来表达,但习惯上我们称决策变量、约束条件、目标函数为规划问题的三要素。这个问题的目标和约束都是决策变量的一次表达式,称为线性规划。
案例2 路灯照亮问题(一个非线性规划问题)
如图所示,在一条s=20m宽的道路两侧,分别安装了一只2kw和一只3kw的路灯,它们离地面的高度分别为h1=5m和h2=6m。
- 在漆黑的夜晚,当两只路灯开启时,两只路灯连线路面上最暗的点和最亮的点在哪里?
- 如果3kw路灯的高度可以在3m到9m之间变化,如何求得路面上最暗和最亮的点的位置?
- 如果两只路灯的高度均可以在3m到9m之间变化,结果将如何?

【问题分析】 经验:(物理学背景知识)
这种问题一般人没有相应的物理知识,所以就要去查阅相关资料和文献,来找到相关说明,这一点经常遇到,是十分重要的。
光源点P1在点x处的照度(照亮强度)I1,I1与功率P1成正例,与距离r1的平方成反比,与照射角度α1的正弦成正比。即
其中,k为比例系数,同时也是平衡量纲(单位)的量。
平衡量纲是指在物理学和工程学中,描述物理量的量纲间的平衡关系。物理量的量纲是利用基本物理量(如长度、质量、时间等)的组合来表示的。平衡量纲要求在一个数学表达式中,所有参与运算的物理量具有相同的量纲。
例如,一维运动中的位移、速度和加速度分别具有长度(L)、速度(LT⁻¹)和加速度(LT⁻²)的量纲。在平衡量纲的要求下,相互直接参与运算的位移、速度和加速度必须具有相同的量纲,才能保证运算的准确性。
通过平衡量纲,可以判断一个方程是否正确,检查方程中是否存在错误的物理量单位组合,或者判断未知物理量的量纲。平衡量纲也在工程设计和实验研究中起着重要的作用,保证设计的可行性和实验的准确性。
【问题假设】
- p1,p2都可以看成点光源;
- p1,p2在x的照度可以叠加(求和);
- 光源只来自两盏灯。
【符号设置】
(符号设置如上图所示)
- I : 某点处的照度(亮度);
- I1:灯P1在该点处的照度;
- I2:灯P2在该点处的照度;
- s : 街道宽;
- p1,p2: 两个光源的功率;
- h1,h2: 两盏灯的高度;
- r1,r2: 两盏路灯到x的距离;
- x : 街道某点的坐标,介于0和s之间;
- α1, α2: 光线的入射角。
【建立模型】
两只灯在点x处的照度为:![]()
其中,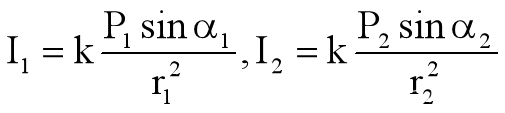
变量之间的关系

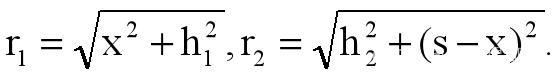
问题(1):灯高度不变,求路面照度最弱最强的位置x。
数学模型1
![]()
 也可以化简为
也可以化简为

代入已知参数,模型简化为

即求一元函数I(x)在[0,20]上的最大值与最小值。
问题(2):当3kw的灯的高度在3m到9m之间变化时,路面的最暗和最亮点。
数学模型2

即求二元函数I(x,h2)在所给矩形闭区域上的最大值与最小值。
问题(3):两只灯的高度都在3m到9m之间变化时,求路面的最暗和最亮点。
数学模型3

即求三元函数I(x,h1,h2)在所给条件下的上的最大值与最小值。
像这种目标函数或者约束条件是决策变量的非一次(非线性)的规划模型,称为非线性规划模型。