梯度下降的几何形式

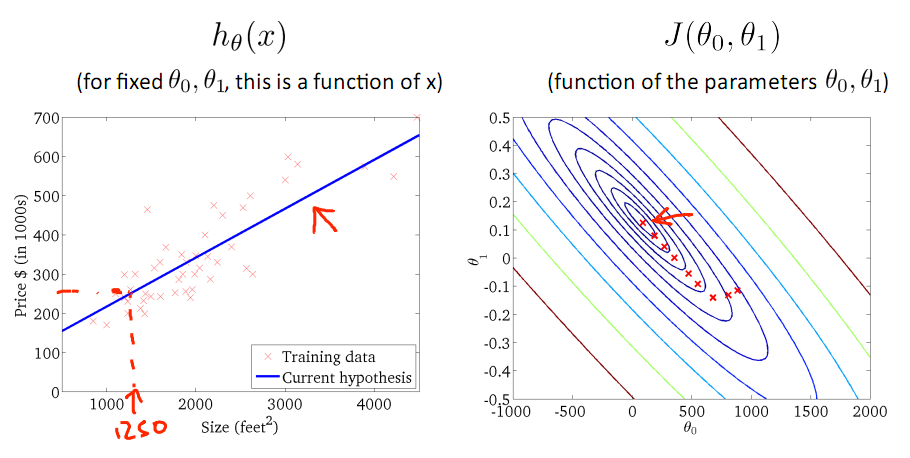
下图为梯度下降的目的，找到J（θ）的最小值。

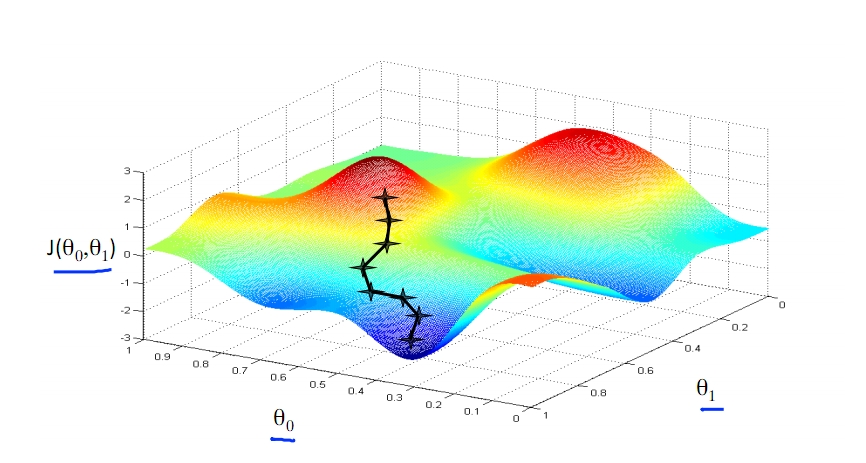
其实，J(θ)的真正图形是类似下面这样的，因为其是一个凸函数，只有一个全局最优解，所以不必担心像上图一样找到局部最优解

直到了要找到图形中的最小值之后，下面介绍自动求解最小值的办法，这就是梯度下降法

对参数向量θ中的每个分量θ_j，迭代减去速率因子a* (dJ(θ)/dθ_j)即可，后边一项为J(θ)关于θ_j的偏导数

3 梯度下降的原理

导数的概念

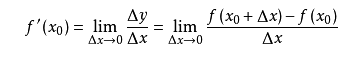
由公式可见，对点x₀的导数反映了函数在点x₀处的瞬时变化速率，或者叫在点x₀处的斜度。推广到多维函数中，就有了梯度的概念，梯度是一个向量组合，反映了多维图形中变化速率最快的方向。

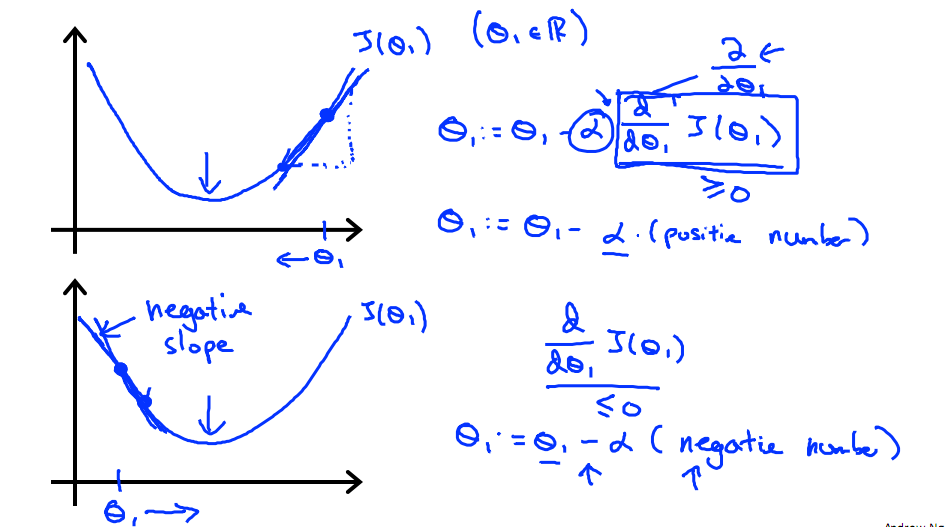
下图展示了对单个特征θ₁的直观图形，起始时导数为正，θ₁减小后并以新的θ₁为基点重新求导，一直迭代就会找到最小的θ_1，若导数为负时，θ₁的就会不断增到，直到找到使损失函数最小的值。

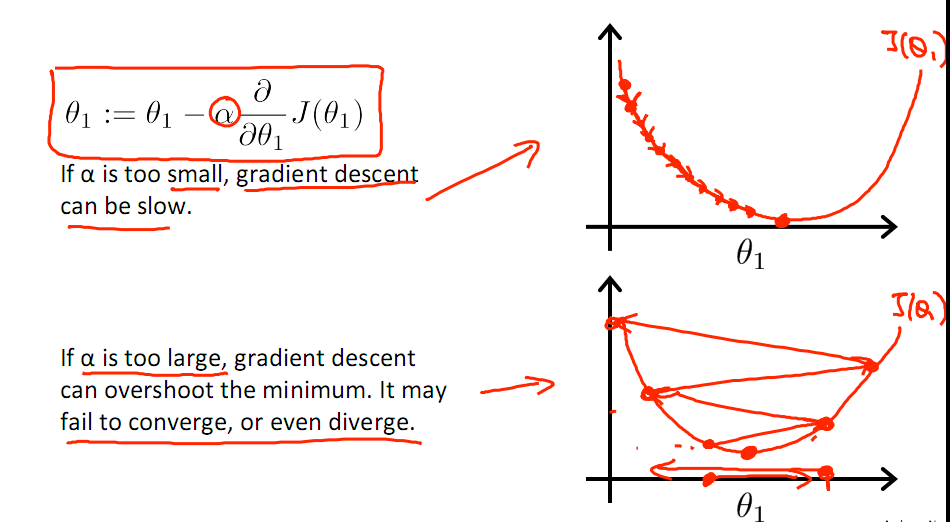
有一点需要注意的是步长a的大小，如果a太小，则会迭代很多次才找到最优解，若a太大，可能跳过最优，从而找不到最优解。

另外，在不断迭代的过程中，梯度值会不断变小，所以θ₁的变化速度也会越来越慢，所以不需要使速率a的值越来越小

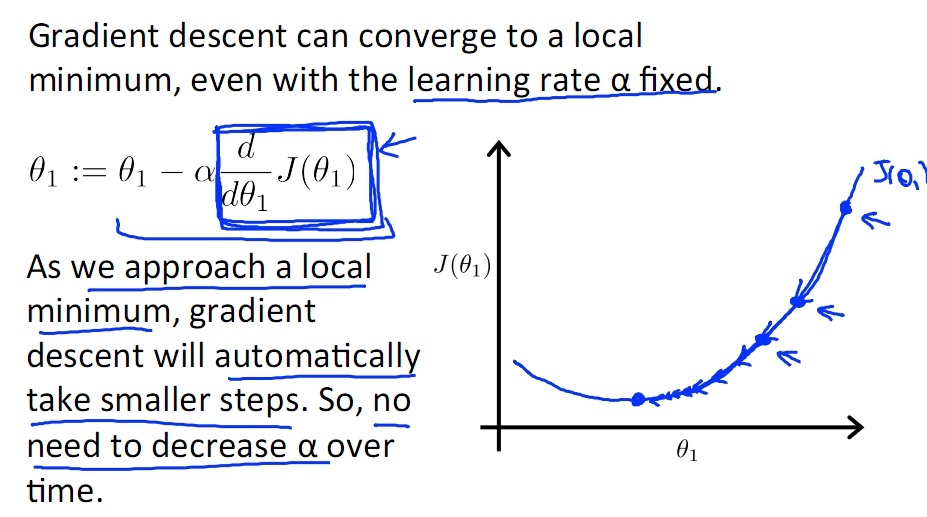
下图就是寻找过程

当梯度下降到一定数值后，每次迭代的变化很小，这时可以设定一个阈值，只要变化小鱼该阈值，就停止迭代，而得到的结果也近似于最优解。

若损失函数的值不断变大，则有可能是步长速率a太大，导致算法不收敛，这时可适当调整a值

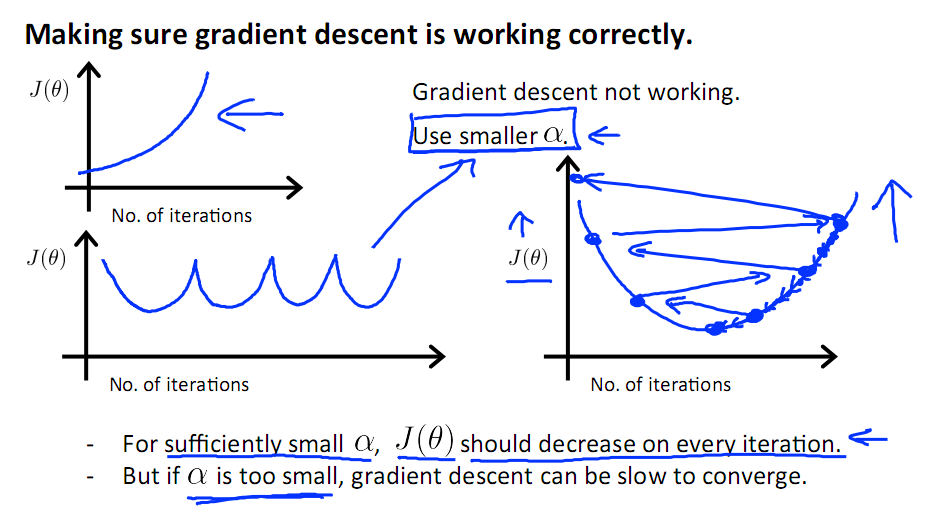
为了选择参数a，就需要不断测试，因为a太大太小都不太好。

import numpy as np
import matplotlib.pyplot as plt
x=np.linspace(-1,6,141)
y=(x-2.5)**2-1
#每点梯度
def dj(theta):
    return 2*(theta-2.5)
#每点的Y值
def J(theta):
    try:
        return (theta-2.5)**2-1
    #防止J越来越大
    except:
        return float('inf')
#梯度下降，将theta的值记录下来，定义最大迭代次数和允许的最小误差
def gradient_descent(initial_theta,eta,n_iters=1e4,error=1e-8):
    theta=initial_theta
    theta_hist.append(initial_theta)
    i_iter=0
    while i_iter<n_iters:
        gradient=dj(theta)
        last_theta=theta
        theta=theta-eta*gradient
        theta_hist.append(theta)
        if abs(J(theta)-J(last_theta))<error:
            break
        i_iter+=1
#绘制原始曲线和梯度下降过程
def plot_thetahist():
    plt.plot(x,J(x))
    plt.plot(np.array(theta_hist),J(np.array(theta_hist)),color='r',marker='+')
    plt.show()

#学习率,步长
eta=0.1
theta_hist=[]
gradient_descent(0,eta,n_iters=10)
plot_thetahist()

eta=0.1

eta=0.01

eta=1.1