1. 线性插值方法

1.1 最近邻算法 (Nearest Neighbor Interpolation)

上图是一个一维的最近邻插值的示意图，坐标轴上各点 xi-1，xi，xi+1 … 两两对半等分间隔 (红色虚线划分)，从而非边界的各坐标点都有一个等宽的邻域，并根据每个坐标点的值构成一个类似分段函数的函数约束，从而使各插值坐标点的值等同于所在邻域原坐标点的值。例如，插值点 x 坐落于 坐标点 xi 的邻域，那么其值 f(x) 就等于 f(xi)。

上图是一个二维最近邻插值的定量俯视示意图，(x0, y0)、(x0, y1)、(x1, y0)、(x1, y1) 都是原图像上的坐标点，灰度值分别对应为 Q11、Q12、Q21、Q22。而灰度值未知的插值点 (x, y)，根据最近邻插值方法的约束，其与坐标点 (x0, y0) 位置最接近 (即位于 (x0, y0) 的邻域内)，故插值点 (x, y) 的灰度值 P = Q11。

1.2 线性插值 (Linear Interpolation)

上图是一个一维的线性插值的定性示意图，坐标轴上各点 xi-1，xi，xi+1 … 的值“两两直接相连”为线段，从而构成了一条连续的约束函数。而插值坐标点例如 x，根据约束函数其值应为 f(x)。因为每两个坐标点之间的约束函数曲线是一次线性的线段，对插值结果而言是“线性” 的，所以该方法称为线性插值。

上图是一个一维线性插值的定量示意图，x0 和 x1 都是原有的坐标点，灰度值分别对应为 y0 和 y1。而灰度值未知的插值点 x，根据线性插值法约束，在 (x0, y0) 和 (x1, y1) 构成的一次函数上，其灰度值 y 即为：
$$y=y_0+\left(x-x_0\right)\frac{y_1-y_0}{x_1-x_0}=y_0+\frac{\left(x-x_0\right)y_1-\left(x-x_0\right)y_0}{x_1-x_0}$$

1.3 双线性插值算法 (Bilinear Interpolation)

由一维的线性插值很容易拓展到二维图像的双线性插值，每次需要要经过三次一阶线性插值才能获得最终结果，上图便展示了该过程的一种定性斜视示意图。其中，(x0, y0)、(x0, y1)、(x1, y0)、(x1, y1) 均为原图像上的像素坐标点，灰度值分别对应为 f(x0, y0)、f(x0, y1)、f(x1, y0)、f(x1, y1)。而灰度值未知的插值点 (x, y)，根据双线性插值法的约束，可以先由像素坐标点 (x0, y0) 和 (x0, y1) 在 y 轴向作一维线性插值得到 f(x0, y)、由像素坐标点 (x1, y0) 和 (x1, y1) 在 y 轴向作一维线性插值得到 f(x1, y)，然后再由 (x0, y) 和 (x1, y) 在 x 轴向作一维线性插值得到插值点 (x, y) 的灰度值 f(x, y)。当然，一维线性插值先作 x 轴向再作 y 轴向，得到的结果完全相同，仅为顺序先后的区别，例如：

上图是一个二维双线性插值的定量俯视示意图 (点位稍有变动但不影响)，我们换个顺序。先由像素坐标点 (x0, y0) 和 (x1, y0) 在 x 轴向作一维线性插值得到 f(x, y0)、由像素坐标点 (x0, y1) 和 (x1, y1) 在 x 轴向作一维线性插值得到 f(x, y1)：
$$\begin{array}{rl}& f\left(x,y_0\right)=\frac{x_1-x}{x_1-x_0}f\left(x_0,y_0\right)+\frac{x-x_0}{x_1-x_0}f\left(x_1,y_0\right)\\ & f\left(x,y_1\right)=\frac{x_1-x}{x_1-x_0}f\left(x_0,y_1\right)+\frac{x-x_0}{x_1-x_0}f\left(x_1,y_1\right)\end{array}$$
然后再由 (x, y0) 和 (x, y1) 在 y 轴向作一维线性插值得到插值点 (x, y) 的灰度值 f(x, y)：

$$f(x,y)=\frac{y_1-y}{y_1-y_0}f\left(x,y_0\right)+\frac{y-y_0}{y_1-y_0}f\left(x,y_1\right)$$

合并上式，得到最终的双线性插值结果：
$$f(x,y)=\frac{\left(y_1-y\right)\left(x_1-x\right)}{\left(y_1-y_0\right)\left(x_1-x_0\right)}f\left(x_0,y_0\right)+\frac{\left(y_1-y\right)\left(x-x_0\right)}{\left(y_1-y_0\right)\left(x_1-x_0\right)}f\left(x_1,y_0\right)+\frac{\left(y-y_0\right)\left(x_1-x\right)}{\left(y_1-y_0\right)\left(x_1-x_0\right)}f\left(x_0,y_1\right)+\frac{\left(y-y_0\right)\left(x-x_0\right)}{\left(y_1-y_0\right)\left(x_1-x_0\right)}$$

1.4 双三次插值算法(Bicubic Interpolation)

又称 立方卷积插值 / 双立方插值，在数值分析中，双三次插值是二维空间中最常用的插值方法。在这种方法中，插值点 (x, y) 的像素灰度值 f(x, y) 通过矩形网格中 最近的十六个采样点的加权平均 得到，而 各采样点的权重由该点到待求插值点的距离确定，此距离包括 水平和竖直 两个方向上的距离。相比之下，双线性插值则由周围的四个采样点加权得到。

上图是一个二维图像的双三次插值俯视示意图。设待求插值点坐标为 (i+u, j+v)，已知其周围的 16 个像素坐标点 (网格) 的灰度值，还需要计算 16 个点各自的权重。以像素坐标点 (i, j) 为例，因为该点在 y 轴和 x 轴方向上与待求插值点 (i+u, j+v) 的距离分别为 u 和 v，所以的权重为 w(u) × w(v)，其中 w(·) 是插值权重核 (可以理解为定义的权重函数)。同理可得其余 15 个像素坐标点各自的权重。那么，待求插值点 (i+u, j+v) 的灰度值 f(i+u, j+v) 将通过如下计算得到：
$$f(i+u,j+v)=A\times B\times C$$
其中各项由向量或矩阵表示为：
$$\begin{array}{c}\mathrm{A}=\left[\begin{array}{llll}w(1+u)& w(u)& w(1-u)& w(2-u)\end{array}\right]\\ \mathrm{B}=\left[\begin{array}{llll}f(i-1,j-1)& f(i-1,j+0)& f(i-1,j+1)& f(i-1,j+2)\\ f(i+0,j-1)& f(i+0,j+0)& f(i+0,j+1)& f(i+0,j+2)\\ f(i+1,j-1)& f(i+1,j+0)& f(i+1,j+1)& f(i+1,j+2)\\ f(i+2,j-1)& f(i+2,j+0)& f(i+2,j+1)& f(i+2,j+2)\end{array}\right]\\ \mathrm{C}={\left[\begin{array}{llll}w(1+v)& w(v)& w(1-v)& w(2-v)\end{array}\right]}^T\end{array}$$
插值权重核 w(·) 为BiCubic函数：
$$w(x)=\{\begin{array}{cc}1-2|x{|}^2+|x{|}^3& ,|x|<1\\ 4-8|x|+5|x{|}^2-|x{|}^3,& 1\le |x|<2\\ 0& |x|\ge 2\end{array}$$
其函数图像如下所示：

2. 深度学习

2.1 反卷积/转置卷积 (Deconvolution/Transposed Convolution)

详见：深度学习中的卷积操作
下图是2x2的卷积核，stride=1时的转置卷积。

核张量与输入的张量中，逐个元素相乘，放在对应的地方。就是说第一个元素是0，就是0乘上整个核张量，放在对应的位置。第二个元素是1则是乘上核张量放在对应滑动到下一个位置。以此类推。得到四个图，将四个图相加即可得出最终输出。此处的例子stride为1，所以滑动的步长是1。
总结出来的公式为：
$$\mathrm{Y}[\mathrm{i}:\mathrm{i}+\mathrm{h},\mathrm{j}:\mathrm{j}+\mathrm{w}]+=\mathrm{X}[\mathrm{i},\mathrm{j}]\ast \mathrm{K}$$
其中Y的大小就是卷积的大小计算公式反过来：
卷积： $out=(Input-kernel+2\ast padding)/stride+1$
反卷积： $out=(Input-1)\ast stride+kernel-2\ast padding$

• Stride
  Stride就是滑动的步长。
  下图是2x2的卷积核，stride=2时的转置卷积。
  

• Padding
  与常规卷积不同，在转置卷积中，填充被应用于的输出（常规卷积将填充应用于输入）。 例如，当将高和宽两侧的填充数指定为1时，转置卷积的输出中将删除第一和最后的行与列。

2.2 反池化(Unpooling)

反池化是池化的逆操作，一般来说有三种反池化的方法

• Nearest Neighbor，就是把相同的数据复制４个达到扩大四倍的效果。这个方法也叫做反平均池化。
  

• Bed of Nails
  把数据放在在对应位置的左上角，然后其余的地方补0
  

• MaxUnpooling
  要求在池化过程中记录最大激活值的坐标位置，然后还原原来的大小，在反池化时，只要把池化过程中最大激活值所在位置坐标激活，其他的值设置为 0。当然，这个过程只是一种近似。因为在池化过程中，除了最大值的位置，其他的值也是不全为 0 的。
  

2.3 亚像素卷积（PixelShuffle）

ESPCN第一次提出PixelShuffle算法，详见：超分算法ESPCN：《Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel》

亚像素卷积的核心思想：一张图像放大r倍，就相当于每个像素都放大r倍。

在网络倒数第二层卷积过程输出通道数为r^2与原图同样大小的特征图像
然后经过亚像素卷积层周期性排列，得到大小为(w × r , h × r) 的重建图像。

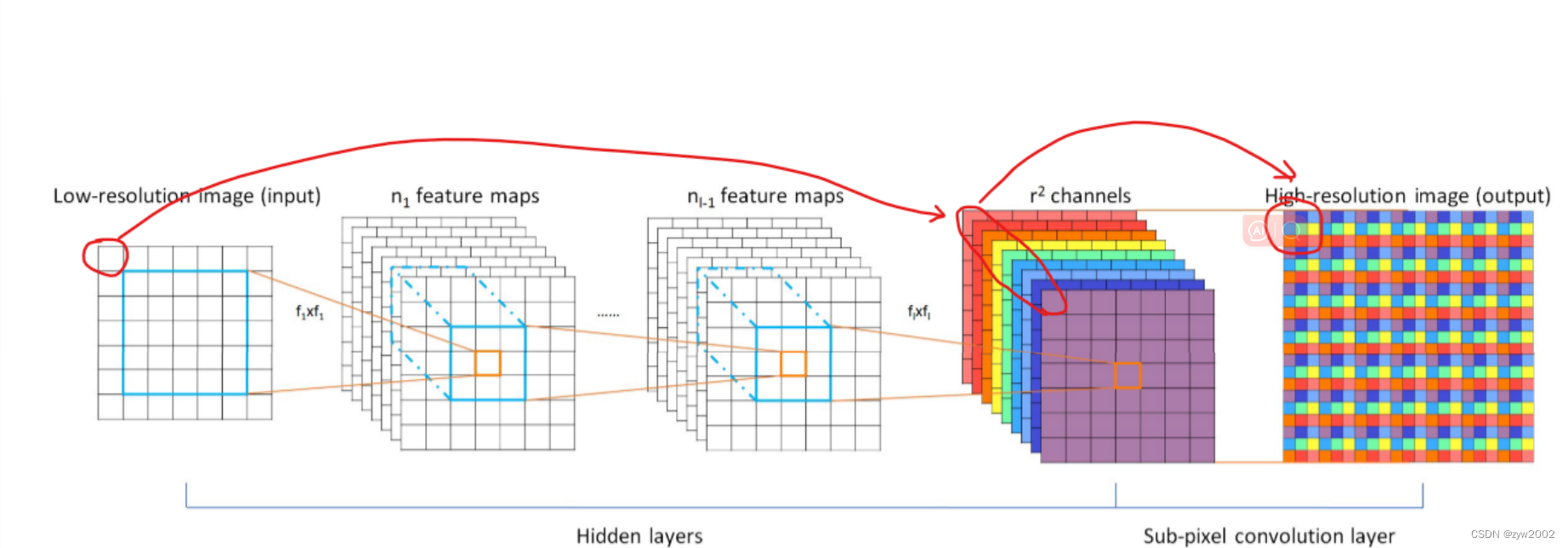
如上图中倒数第二层红圈框住的9个特征，排列后组成箭头所指的最后一层小方框，这就是原图中框住的像素经过网络构成的重建块。这九个像素刚好使原像素的长宽各放大了三倍。
亚像素卷积（Sub-pixel Convolution）其实并没有卷积运算，只是抽取特征然后进行简单排列。

3. 在SR中的应用

超分任务中上采样的几种方法：

1. 双三次插值作为基础，使用卷积层进行微调修正。DCSCN
2. 反卷积层，使用pangding的方式扩大图像。SRDenseNet
3. 使用步长为$\frac{1}{r}$ 的反卷积，放大图像。FSRCNN
4. 亚像素卷积，不需要额外计算量的隐式卷积层，通过重排来构建输出。ESPCN

4. 参考

【1】【图像处理】详解 最近邻插值、线性插值、双线性插值、双三次插值
【2】关于上采样方法总结（插值和深度学习）