logistic回归参数更新看了几篇博文，感觉理解不透彻，所以自己写一下，希望能有更深的理解。logistic回归输入是一个线性函数$\mathbf{W}\mathbf{x}+\mathbf{b}$，为了简单理解，考虑batchsize为1的情况。这时输入$\mathbf{x}$为一个$n\times 1$的向量，标签$\mathbf{y}$我们采用oneHot编码为一个$m\times 1$的向量，显然\boldsymbol{b}也是一个$m\times 1$的向量，参数$\mathbf{W}$为一个$m\times n$的矩阵。若$n=4$、$m=3$，我们用图形表示logistic回归如下：

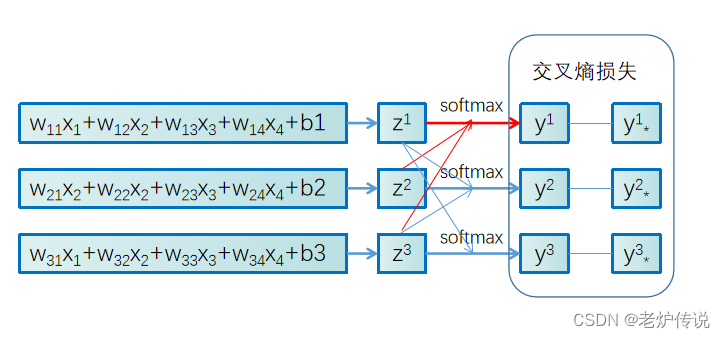
这里的标签$\mathbf{y}$采用onehot编码，长度为3，如果类别编号为1，则其编码为 { 1 , 0 , 0 } T \{1,0,0\}^T { 1,0,0}T，对应上图的话，就是$y_{\ast }^1=1$，$y_{\ast }^2=0$，$y_{\ast }^3=0$。损失函数$L$就是$y^1$和$y_{\ast }^1$的交叉熵损失+$y^2$和$y_{\ast }^2$的交叉熵损失+$y^3$和$y_{\ast }^3$的交叉熵损失。
$$\begin{array}{rl}L& =\sum _{i=1}^3{y}_{\ast }^i\log y^i\\ & =y_{\ast }^1\log y^1+y_{\ast }^2\log y^2+y_{\ast }^3\log y^3\end{array}$$
上式中：
$$\begin{array}{rl}{y}^1& =\frac{e^{z^1}}{e^{z^1}+e^{z^2}+e^{z^3}}\\ y^2& =\frac{e^{z^2}}{e^{z^1}+e^{z^2}+e^{z^3}}\\ y^3& =\frac{e^{z^3}}{e^{z^1}+e^{z^2}+e^{z^3}}\end{array}$$
而
$$\begin{array}{r}{z}^1={{\mathbf{w}}_1}^T\mathbf{x}+b_1\\ z^2={{\mathbf{w}}_2}^T\mathbf{x}+b_2\\ z^3={{\mathbf{w}}_3}^T\mathbf{x}+b_3\end{array}$$
其中， w 1 = { w 11 , w 12 , w 13 , w 14 } T \boldsymbol{w_1}=\{w_{11},w_{12},w_{13},w_{14}\}^T w1​={ w11​,w12​,w13​,w14​}T， x = { x 1 , x 2 , x 3 , x 4 } T \boldsymbol{x}=\{x_{1},x_{2},x_{3},x_{4}\}^T x={ x1​,x2​,x3​,x4​}T因此：

损失函数$L$对${\mathbf{w}}_1$求导：
$$\begin{array}{rl}\frac{\partial L}{\partial {\mathbf{w}}_1}& =\frac{\partial L}{\partial y_1}\frac{\partial y_1}{\partial z^1}\frac{\partial z^1}{\partial {\mathbf{w}}_1}+\frac{\partial L}{\partial y_2}\frac{\partial y_2}{\partial z^1}\frac{\partial z^1}{\partial {\mathbf{w}}_1}+\frac{\partial L}{\partial y_3}\frac{\partial y_3}{\partial z^1}\frac{\partial z^1}{\partial {\mathbf{w}}_1}\\ & =\frac{y_1^{\ast }}{y_1}\times y_1(1-y_1)\times \mathbf{x}-\frac{y_2^{\ast }}{y_2}\times y_1{y}_2\times \mathbf{x}-\frac{y_3^{\ast }}{y_3}\times y_1{y}_3\times \mathbf{x}\\ & =(y_1^{\ast }(1-y_1)-y_2^{\ast }{y}_1-y_3^{\ast }{y}_1)\mathbf{x}\\ & =(y_1^{\ast }-y_1(y_1^{\ast }+y_2^{\ast }+y_3^{\ast }))\mathbf{x}\\ & =(y_1^{\ast }-y_1)\mathbf{x}\end{array}$$
注意$(y_1^{\ast }+y_2^{\ast }+y_3^{\ast })$是标签onehot编码的三个值，和正好为1。同理可得到剩下的两个导数：
$$\begin{gathered} \frac{\partial L}{\partial {\mathbf{w}}_2}=(y_2^{\ast }-y_2)\mathbf{x} \\ \frac{\partial L}{\partial {\mathbf{w}}_3}=(y_3^{\ast }-y_3)\mathbf{x} \end{gathered}$$
交叉熵损失函数$L$关于$\mathbf{w}$的梯度为：
$${\left[\begin{array}{rlrl}& (y_1^{\ast }-y_1)x1& (y_2^{\ast }-y_2)x1& (y_3^{\ast }-y_3)x1\\ & (y_1^{\ast }-y_1)x2& (y_2^{\ast }-y_2)x2& (y_3^{\ast }-y_3)x2\\ & (y_1^{\ast }-y_1)x3& (y_2^{\ast }-y_2)x3& (y_3^{\ast }-y_3)x3\\ & (y_1^{\ast }-y_1)x4& (y_2^{\ast }-y_2)x4& (y_3^{\ast }-y_3)x4\\ & (y_1^{\ast }-y_1)x5& (y_2^{\ast }-y_2)x5& (y_3^{\ast }-y_3)x5\end{array}\right]}^T$$
这样交叉熵损失函数$L$关于$\mathbf{w}$的梯度用numpy的外积计算表示为：
$$\frac{\partial L}{\partial \mathbf{w}}=numpy.outer(\mathbf{x},{\mathbf{y}}^{\ast }-\mathbf{y})$$
用同样的方法可以推导出：
$$\frac{\partial L}{\partial \mathbf{b}}={\mathbf{y}}^{\ast }-\mathbf{y}$$