文章目录
- 传统CV算法-边缘检测
-
- 第一章 概述
- **第二章 一阶微分边缘算子**
- 第三章 二阶微分边缘算子
- **第四章** SUSAN **边缘及角点检测方法**
- **第五章** ***新兴的边缘检测算法**
- **第六章** **相关代码**
- **第七章** **附录**
传统CV算法-边缘检测
第一章 概述
1. 边缘检测概述
1.1 认识边缘
边缘的定义
- 边缘是不同区域的分界线,是周围(局部)灰度值有显著变化的像素点的集合,有幅值 与方向两个属性。这个不是绝对的定义,边缘是局部特征,以及周围灰度值显著变化会产生边缘。
轮廓和边缘的关系
-
轮廓代表的整体特征,边缘代表局部特征
-
一般认为轮廓是对物体的完整边界的描述,边缘点一个个连接起来构成轮廓。边缘可以 是一段边缘,而轮廓一般是完整的。人眼视觉特性,看物体时一般是先获取物体的轮廓信息, 再获取物体中的细节信息。
-
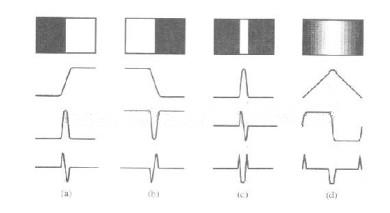
阶跃型、屋脊型、斜坡型、脉冲型
- 区别:变化的快慢不同
- 在边缘检测中更多关注的是阶跃和 屋脊型边缘。
- (a)和(b)可认为是阶跃或斜坡型,(c)脉冲型,(d)屋脊型, 阶跃与屋脊的不同在于阶跃上升或下降到某个值后持续下去,而屋脊则是先上升后下降。
1.2 边缘检测的概念
- 边缘检测是图像处理与计算机视觉中极为重要的一种分析图像的方法
- 目的是找到 图像中亮度变化剧烈的像素点构成的集合,表现出来往往是轮廓。
- 如果图像中边缘能够精确 的测量和定位,那么,就意味着实际的物体能够被定位和测量,包括物体的面积、物体的直 径、物体的形状等就能被测量。在对现实世界的图像采集中,有下面 4 种情况会表现在图像 中时形成一个边缘。
- 深度的不连续(物体处在不同的物平面上);
- 表面方向的不连续(如正方体的不同的两个面);
- 物体材料不同(这样会导致光的反射系数不同);
- 场景中光照不同(如被树萌投向的地面);
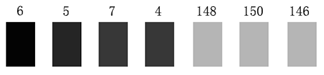
举例:例如上面的图像是图像中水平方向 7 个像素点的灰度值显示效果,我们很容易地判断在 第 4 和第 5 个像素之间有一个边缘,因为它俩之间发生了强烈的灰度跳变。在实际的边缘 检测中,边缘远没有上图这样简单明显,我们需要取对应的阈值来区分出它们。
1.3 边缘检测的基本方法
- 图像滤波
- 传统边缘检测算法主要是基于图像强度的一阶和二阶导数,但导数的计算对噪声很敏感, 因此必须使用滤波器来改善与噪声有关的边缘检测器的性能。
- 大多数滤波器 在降低噪声的同时也造成了边缘强度的损失,因此,在增强边缘和降低噪声之间需要一个 折中的选择。
- 图像增强
- 增强边缘的基础是确定图像各点邻域强度的变化值。
- 增强算法可以将邻域(或局部)强度值有显著变化的点突显出来。
- 边缘增强一般是通过计算梯度的幅值来完成的。
- 图像检测
- 在图像中有许多点的梯度幅值比较大,而这些点在特定的应用领域中并不都是边缘,所以应该用某种检测方法来确定哪些点是边缘点。
- 最简单的边缘检测判断依据是梯度幅值。
- 图像定位
- 如果某一应用场合要求确定边缘位置,则边缘的位置可在子像素分辨率上来估计,边缘 的方位也可以被估计出来。
1.4 边缘检测算子的概念
-
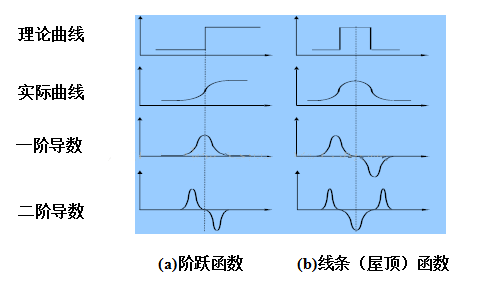
在数学中,函数的变化率由导数来刻画.
-
图像我们看成二维函数,其上面的像素值变化, 当然也可以用导数来刻画,当然图像是离散的,那我们换成像素的差分来实现。
-
边缘检测算子的类型存在一阶和二阶微分算子。对于阶跃型边缘,显示其一阶导数具有极大值,极大值点对应二阶导数的过零点,也就是准确的边缘的位置是对应于一阶导数的极大值点,或者二阶导数的过零点(注意不仅仅是二阶导 数为 0 值的位置,二值正负值过渡的零点)。
1.5 常见的边缘检测算子

-
常见的一阶微分边缘算子包括 Roberts,Prewitt,Sobel,Kirsch 以及 Nevitia
-
常见的 二阶微分边缘算子包括 Laplace 算子,LOG 算子,DOG 算子和 Canny 算子等。其中 Canny
算子是最为常用的一种,也是当前被认为最优秀的边缘检测算子。
- 此外,还有一种边缘检测方法 SUSAN,它没有用到图像像素的梯度(导数)。 以及本文会概述一些新兴的边缘检测方法,如小波分析,模糊算法以及人工神经网络等
2. 用梯度算子实现边缘检测的原理
2.1 认识梯度算子
-
边缘点 :一阶微分幅度的最大值点以及二阶微分的零点。
-
梯度的定义 :个曲面沿着给定方向的倾斜程度,在单变量函数中,梯度只是导数,在线性函数中, 是线的斜率——有方向的向量。
-
梯度算子 :梯度属于一阶微分算子,对应一阶导数。若图像含有较小的噪声并且图像边缘的灰度值过渡较为明显,梯度算子可以得到较好的边缘检测结果。 前篇介绍的 Roberts,Sobel 等算子都属于梯度算子。
2.2 梯度的衡量
对于连续函数 f ( x , y ) \mathrm{f}(\mathrm{x}, \mathrm{y}) f(x,y), 我们计算出了它在 ( x , y ) (\mathrm{x}, \mathrm{y}) (x,y) 处的梯度, 并且用一个矢量 (沿 x \mathrm{x} x 方向和沿 y \mathrm{y} y 方向的两个分量)来表示, 如下:
G ( x , y ) = [ G x G y ] = [ ∂ f ∂ x ∂ f ∂ y ] \mathrm{G}(\mathrm{x}, \mathrm{y})=\left[\begin{array}{l} G_x \\ G_y \end{array}\right]=\left[\begin{array}{l} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{array}\right] G(x,y)=[GxGy]=[∂x∂f∂y∂f]
梯度的幅值衡量, 可以用到以下三种范数:
∣ G ( x , y ) ∣ = G x 2 + G y 2 , 2 范数梯度 ∣ G ( x , y ) ∣ = ∣ G x ∣ + ∣ G y ∣ , 1 范数梯度 ∣ G ( x , y ) ∣ ≈ max ( ∣ G x ∣ , ∣ G y ∣ ) , , ∞ 范数梯度 \begin{gathered} |\mathrm{G}(\mathrm{x}, \mathrm{y})|=\sqrt{G_x^2+G_y^2}, 2 \text { 范数梯度 } \\ |\mathrm{G}(\mathrm{x}, \mathrm{y})|=\left|G_x\right|+\left|G_y\right|, \quad 1 \text { 范数梯度 } \\ |\mathrm{G}(\mathrm{x}, \mathrm{y})| \approx \max \left(\left|G_x\right|,\left|G_y\right|\right), \quad, \quad \infty \text { 范数梯度 } \end{gathered} ∣G(x,y)∣=Gx2+Gy2,2 范数梯度 ∣G(x,y)∣=∣Gx∣+∣Gy∣,1 范数梯度 ∣G(x,y)∣≈max(∣Gx∣,∣Gy∣),,∞ 范数梯度
备注:使用 2 范数梯度要对图像中的每个像素点进行平方及开方运算, 计算 复杂度高, 在实际应用中, 通常取绝对值(1范数)或最大值(无穷范数)来近似代替该运算以实现简化, 与平方及开方运算相比, 取绝对值或最大值进行的边缘检测的准确度和边缘的精度差异都很小。
2.3 使用梯度算子实现边缘检测
原理 基于梯度算子的边缘检测大多数是基于方向导数求卷积的方法
实现过程
以 3×3 的卷积模板为例。
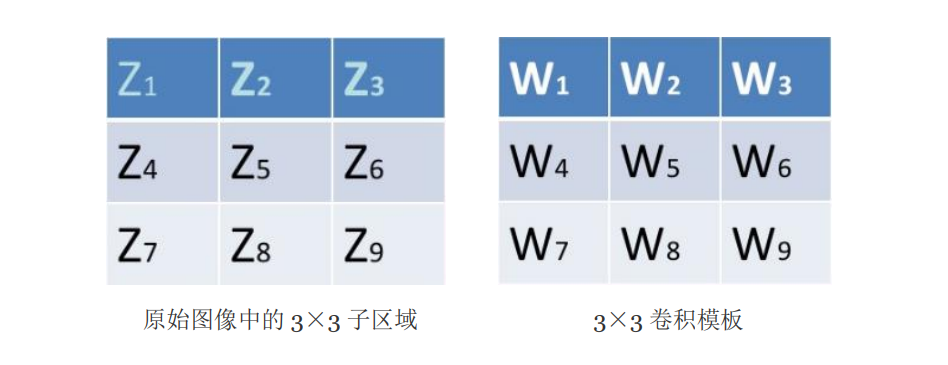
设定好卷积模板后, 将模板在图像中移动, 并将图像中的每个像素点与此模板进行卷积, 得到每个像素点的响应 R \mathrm{R} R, 用 R \mathrm{R} R 来表征每个像素点的邻域灰度值变化率, 即灰度梯度值, 从而可将灰度图像经过与模板卷积后转化为梯度图像。模板系数 W i ( i = 1 , 2 , 3 , ⋯ ⋯ 9 ) W_i(\mathrm{i}=1,2,3, \cdots \cdots 9) Wi(i=1,2,3,⋯⋯9) 相加的 总和必须为零, 以确保在灰度级不变的区域中模板的响应为零。 Z \mathrm{Z} Z 表示像素的灰度值
R = W 1 Z 1 + W 2 Z 2 + ⋯ + W 9 Z 9 \mathrm{R}=W_1 Z_1+W_2 Z_2+\cdots+W_9 Z_9 R=W1Z1+W2Z2+⋯+W9Z9
通过设定一个阈值, 如果卷积的结果 R \mathrm{R} R 大于这个阈值, 那么该像素点为边缘点, 输出白色; 如果 R \mathrm{R} R 小于这个阈值, 那么该像素不为边缘点, 输出黑色。于是最终我们就能输 出一幅黑白的梯度图像, 实现边缘的检测。
第二章 一阶微分边缘算子
1. 一阶微分边缘算子基本思想
一阶微分边缘算子:也称梯度边缘算子, 利用图像在边缘处的阶跃性, 即图像梯度在边缘取得极大值的特性进行边缘检测。梯度是一个矢量, 它具有方向 θ \theta θ 和模 ∣ Δ I ∣ : |\Delta \mathrm{I}|: ∣ΔI∣:
Δ I = ( ∂ I ∂ x ∂ I ∂ y ) ∣ Δ I ∣ = ( ∂ I ∂ x ) 2 + ( ∂ I ∂ y ) 2 = I x 2 + I y 2 θ = arctan ( I y / I x ) \begin{gathered} \Delta I=\left(\begin{array}{c} \frac{\partial I}{\partial x} \\ \frac{\partial I}{\partial y} \end{array}\right) \\ |\Delta I|=\sqrt{\left(\frac{\partial I}{\partial x}\right)^2+\left(\frac{\partial I}{\partial y}\right)^2}=\sqrt{I_x^2+I_y^2} \\ \theta=\arctan \left(I_y / I_x\right) \end{gathered} ΔI=(∂x∂I∂y∂I)∣ΔI∣=(∂x∂I)2+(∂y∂I)2=Ix2+Iy2θ=arctan(Iy/Ix)
-
梯度的方向提供了边缘的趋势信息,梯度方向始终是垂直于边缘方向, 梯度的模值大小提供了边缘的强度信息。
-
在实际使用中, 通常利用有限差分进行梯度近似。对于上面的公式, 我们有如下的近似:
∂ I ∂ x = lim h → 0 I ( x + Δ x , y ) − I ( x , y ) Δ x ≈ I ( x + 1 , y ) − I ( x , y ) , ( Δ x = 1 ) ∂ I ∂ y = lim h → 0 I ( x , y + Δ x y ) − I ( x , y ) Δ y ≈ I ( x , y + 1 ) − I ( x , y ) , ( Δ y = 1 ) \begin{aligned} & \frac{\partial I}{\partial x}=\lim _{h \rightarrow 0} \frac{I(x+\Delta x, y)-I(x, y)}{\Delta x} \approx I(x+1, y)-I(x, y),(\Delta x=1) \\ & \frac{\partial I}{\partial y}=\lim _{h \rightarrow 0} \frac{I(x, y+\Delta x y)-I(x, y)}{\Delta y} \approx I(x, y+1)-I(x, y),(\Delta y=1) \end{aligned} ∂x∂I=h→0limΔxI(x+Δx,y)−I(x,y)≈I(x+1,y)−I(x,y),(Δx=1)∂y∂I=h→0limΔyI(x,y+Δxy)−I(x,y)≈I(x,y+1)−I(x,y),(Δy=1)
2. Roberts 算子
2.1 Roberts算法思想
- 2x2 的模 板,采用的是对角方向相邻的两个像素之差。
- 从图像处理的实际效果来看,边缘定位较准,对噪声敏感。
由 Roberts 提出的算子是一种利用局部差分算子寻找边缘的算子, 边缘的锐利程度由图像灰度的梯度决定。梯度是一个向量, ∇ f \nabla \mathrm{f} ∇f 指出灰度变化的最快的方向和数量。
因此最简单的边缘检测算子是用图像的垂直和水平差分来逼近梯度算子:
∇ f = ( f ( x , y ) − f ( x − 1 , y ) , f ( x , y ) − f ( x , y − 1 ) ) \nabla f=(f(x, y)-f(x-1, y), f(x, y)-f(x, y-1)) ∇f=(f(x,y)−f(x−1,y),f(x,y)−f(x,y−1))
对每一个像素计算出以上式子的向量, 求出它的绝对值, 然后与阈值进行比较, 利用这种思想就得到了 Roberts 交叉算子:
g ( i , j ) = ∣ f ( i , j ) − f ( i + 1 , j + 1 ) ∣ + ∣ f ( i , j + 1 ) − f ( i + 1 , j ) ∣ g(i, j)=|f(i, j)-f(i+1, j+1)|+|f(i, j+1)-f(i+1, j)| g(i,j)=∣f(i,j)−f(i+1,j+1)∣+∣f(i,j+1)−f(i+1,j)∣
2.2 Roberts算法步骤
- 选用 1 范数梯度计算梯度幅度:
∣ G ( x , y ) ∣ = ∣ G x ∣ + ∣ G y ∣ , 1 范数梯度 \begin{gathered} |\mathrm{G}(\mathrm{x}, \mathrm{y})|=\left|G_x\right|+\left|G_y\right|, \quad 1 \text { 范数梯度 } \end{gathered} ∣G(x,y)∣=∣Gx∣+∣Gy∣,1 范数梯度
- 卷积模板为:
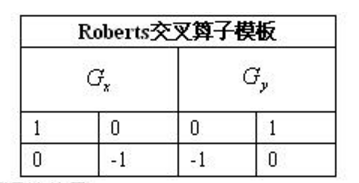
G x = 1 ∗ f ( x , y ) + 0 ∗ f ( x + 1 , y ) + 0 ∗ f ( x , y + 1 ) + ( − 1 ) ∗ f ( x + 1 , y + 1 ) = f ( x , y ) − f ( x + 1 , y + 1 ) G y = 0 ∗ f ( x , y ) + 1 ∗ f ( x + 1 , y ) + ( − 1 ) ∗ f ( x , y + 1 ) + 0 ∗ f ( x + 1 , y + 1 ) = f ( x + 1 , y ) − f ( x , y + 1 ) G ( x , y ) = ∣ G x ∣ + ∣ G y ∣ = ∣ f ( x , y ) − f ( x + 1 , y + 1 ) ∣ + ∣ f ( x + 1 , y ) − f ( x , y + 1 ) \begin{aligned} & G_x=1^* f(x, y)+0^* f(x+1, y)+0^* f(x, y+1)+(-1) * f(x+1, y+1) \\ & =f(x, y)-f(x+1, y+1) \\ & G_y=0^* f(x, y)+1^* f(x+1, y)+(-1) * f(x, y+1)+0^* f(x+1, y+1) \\ & =f(x+1, y)-f(x, y+1) \\ & G(x, y)=\left|G_x\right|+\left|G_y\right|=|f(x, y)-f(x+1, y+1)|+\mid f(x+1, y)-f(x, y+1) \end{aligned} Gx=1∗f(x,y)+0∗f(x+1,y)+0∗f(x,y+1)+(−1)∗f(x+1,y+1)=f(x,y)−f(x+1,y+1)Gy=0∗f(x,y)+1∗f(x+1,y)+(−1)∗f(x,y+1)+0∗f(x+1,y+1)=f(x+1,y)−f(x,y+1)G(x,y)=∣Gx∣+∣Gy∣=∣f(x,y)−f(x+1,y+1)∣+∣f(x+1,y)−f(x,y+1)
如果 G ( x , y ) \mathrm{G}(\mathrm{x}, \mathrm{y}) G(x,y) 大于某一阈值, 则我们认为 ( x , y ) (\mathrm{x}, \mathrm{y}) (x,y) 点为边缘点。
2.3 2.3 2.3 Roberts 算子的推导
∂ f ∂ x ≈ f ( x + 1 , y ) − f ( x , y ) ≈ f ( x + 1 , y + 1 ) − f ( x , y + 1 ) ∂ f ∂ y ≈ f ( x , y + 1 ) − f ( x , y ) ≈ f ( x + 1 , y + 1 ) − f ( x + 1 , y ) ∥ ∇ f ( x , y ) ∥ = ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 ≈ ∣ ∂ f ∂ x ∣ + ∣ ∂ f ∂ y ∣ ≈ ∂ f ∂ x + ∂ f ∂ y ≈ f ( x + 1 , y ) − f ( x , y ) + f ( x + 1 , y + 1 ) − f ( x + 1 , y ) = f ( x + 1 , y + 1 ) − f ( x , y ) ≈ ∂ f ∂ x − ∂ f ∂ y ≈ f ( x + 1 , y ) − f ( x , y ) − ( f ( x , y + 1 ) − f ( x , y ) ) = f ( x + 1 , y ) − f ( x , y + 1 ) ≈ ∂ f ∂ y − ∂ f ∂ x ≈ f ( x , y + 1 ) − f ( x , y ) − ( f ( x + 1 , y ) − f ( x , y ) ) = f ( x , y + 1 ) − f ( x + 1 , y ) ≈ − ∂ f ∂ x − ∂ f ∂ y ≈ − ( f ( x + 1 , y ) − f ( x , y ) ) − ( f ( x + 1 , y + 1 ) − f ( x + 1 , y ) ) = f ( x , y ) − f ( x + 1 , y + 1 ) \begin{aligned} & \frac{\partial f}{\partial x} \approx f(x+1, y)-f(x, y) \approx f(x+1, y+1)-f(x, y+1) \\ & \frac{\partial f}{\partial y} \approx f(x, y+1)-f(x, y) \approx f(x+1, y+1)-f(x+1, y) \\ & \|\nabla f(x, y)\|=\sqrt{\left(\frac{\partial f}{\partial x}\right)^2+\left(\frac{\partial f}{\partial y}\right)^2} \approx\left|\frac{\partial f}{\partial x}\right|+\left|\frac{\partial f}{\partial y}\right| \\ & \approx \frac{\partial f}{\partial x}+\frac{\partial f}{\partial y} \approx f(x+1, y)-f(x, y)+f(x+1, y+1)-f(x+1, y)=f(x+1, y+1)-f(x, y) \\ & \approx \frac{\partial f}{\partial x}-\frac{\partial f}{\partial y} \approx f(x+1, y)-f(x, y)-(f(x, y+1)-f(x, y))=f(x+1, y)-f(x, y+1) \\ & \approx \frac{\partial f}{\partial y}-\frac{\partial f}{\partial x} \approx f(x, y+1)-f(x, y)-(f(x+1, y)-f(x, y))=f(x, y+1)-f(x+1, y) \\ & \approx-\frac{\partial f}{\partial x}-\frac{\partial f}{\partial y} \approx-(f(x+1, y)-f(x, y))-(f(x+1, y+1)-f(x+1, y))=f(x, y)-f(x+1, y+1) \end{aligned} ∂x∂f≈f(x+1,y)−f(x,y)≈f(x+1,y+1)−f(x,y+1)∂y∂f≈f(x,y+1)−f(x,y)≈f(x+1,y+1)−f(x+1,y)∥∇f(x,y)∥=(∂x∂f)2+(∂y∂f)2≈ ∂x∂f + ∂y∂f ≈∂x∂f+∂y∂f≈f(x+1,y)−f(x,y)+f(x+1,y+1)−f(x+1,y)=f(x+1,y+1)−f(x,y)≈∂x∂f−∂y∂f≈f(x+1,y)−f(x,y)−(f(x,y+1)−f(x,y))=f(x+1,y)−f(x,y+1)≈∂y∂f−∂x∂f≈f(x,y+1)−f(x,y)−(f(x+1,y)−f(x,y))=f(x,y+1)−f(x+1,y)≈−∂x∂f−∂y∂f≈−(f(x+1,y)−f(x,y))−(f(x+1,y+1)−f(x+1,y))=f(x,y)−f(x+1,y+1)
2.4 Roberts算法优缺点
- 利用局部差分算子寻找边缘,边缘定位精度高,但容易丢失一部分边缘,
- 同时由于图像没有经过平滑处理,因此不具备抑制噪声能力。
- 该算子对具有陡峭边缘且含有噪声少的图像处理效果较好。
- 由于该检测算子模板没有中心点(2X2卷积模板),所以它在实际中很少 使用。
3. Prewitt 算子
3.1 Prewitt算法思想
- 采用了 3*3 大小的卷积模板(2x2大小的模板在概念上很简单,但是他们对于关于中心点对称的模板来计算边缘方向不是很有用,其最小模板大小为3x3。3x3 模板考虑了中心点对段数据的性质,并携带有关于边缘方向的更多信息。)
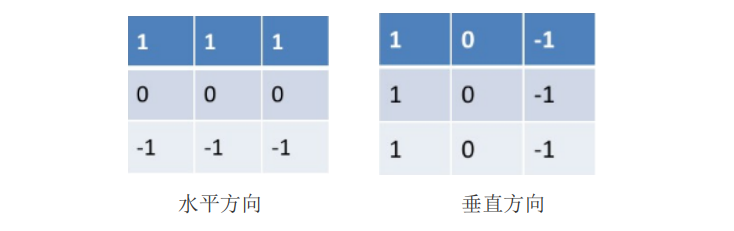
- 在算子的定义上,Prewitt 希望通过使用水平+垂直的两个有向算子去逼近两个偏导数 G X G_X GX, G y G_y Gy,这样在灰度值变化很大的区域上卷积结果也同样达到极大值。
3.2 Prewitt算法步骤
Prewitt 边缘检测算子使用两个有向算子(水平 + + + 垂直), 每一个逼近一个偏导数, 这是 一种类似计算偏微分估计值的方法, x , y \mathrm{x}, \mathrm{y} x,y 两个方向的近似检测算子为: 、
p x = { f ( i + 1 , j − 1 ) + f ( i + 1 , j ) + f ( i + 1 , j + 1 ) } − { f ( i − 1 , j − 1 ) + f ( i − 1 , j ) + f ( i − 1 , j + 1 ) } p y = { f ( i − 1 , j + 1 ) + f ( i , j + 1 ) + f ( i + 1 , j + 1 ) } − { f ( i − 1 , j − 1 ) + f ( i , j − 1 ) + f ( i + 1 , j − 1 ) } \begin{aligned} p_x= & \{f(i+1, j-1)+f(i+1, j)+f(i+1, j+1)\} \\ & -\{f(i-1, j-1)+f(i-1, j)+f(i-1, j+1)\} \\ p_y= & \{f(i-1, j+1)+f(i, j+1)+f(i+1, j+1)\} \\ & -\{f(i-1, j-1)+f(i, j-1)+f(i+1, j-1)\} \end{aligned} px=py={
f(i+1,j−1)+f(i+1,j)+f(i+1,j+1)}−{
f(i−1,j−1)+f(i−1,j)+f(i−1,j+1)}{
f(i−1,j+1)+f(i,j+1)+f(i+1,j+1)}−{
f(i−1,j−1)+f(i,j−1)+f(i+1,j−1)}
得出卷积模板为:
G x = ∣ − 1 0 1 − 1 0 1 − 1 0 1 ∣ G y = ∣ − 1 − 1 − 1 0 0 0 1 1 1 ∣ G_x=\left|\begin{array}{ccc} -1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1 \end{array}\right| \quad G_y=\left|\begin{array}{ccc} -1 & -1 & -1 \\ 0 & 0 & 0 \\ 1 & 1 & 1 \end{array}\right| Gx=
−1−1−1000111
Gy=
−101−101−101
记图像 M \mathrm{M} M, 梯度幅值 T \mathrm{T} T, 比较
T = ( M ⊗ G x ) 2 + ( M ⊗ G y ) 2 > threshold T=\left(M \otimes G_x\right)^2+\left(M \otimes G_y\right)^2>\text { threshold } T=(M⊗Gx)2+(M⊗Gy)2> threshold
如果最终 T \mathrm{T} T 大于阈值 threshold, 那么该点为边缘点。
3.3 Prewitt算法优缺点
- Prewitt 算子对灰度渐变和噪声较多的图像处理效果较好
- 但不能完全排除检测结果中出现的虚假边缘。
4. Sobel 算子
4.1 Sobel算法思想
- 邻域的像素对当前像素产生的影响不是等价的, 所以距离不同的像素具有不同的权值,对算子结果产生的影响也不同。一般来说,距离越远, 产生的影响越小。
- 将 Prewitt 边缘检测算子模板的中心系数增加一个权值 2,不但可以突出中心像素点, 而且可以得到平滑的效果,这就成为索贝尔算子。
4.2 Sobel算法步骤
Sobel 算子一种将方向差分运算与局部平均相结合的方法。该算子是在以 f ( x , y ) \mathrm{f}(\mathrm{x}, \mathrm{y}) f(x,y) 为中心 的 3 × 3 3 \times 3 3×3 邻域上计算 x x x 和 y y y 方向的偏导数, 即
p x = { f ( i + 1 , j − 1 ) + 2 f ( i + 1 , j ) + f ( i + 1 , j + 1 ) } − { f ( i − 1 , j − 1 ) + 2 f ( i − 1 , j ) + f ( i − 1 , j + 1 ) } p y = { f ( i − 1 , j + 1 ) + 2 f ( i , j + 1 ) + f ( i + 1 , j + 1 ) } − { f ( i − 1 , j − 1 ) + 2 f ( i , j − 1 ) + f ( i + 1 , j − 1 ) } \begin{aligned} p_x= & \{f(i+1, j-1)+2 f(i+1, j)+f(i+1, j+1)\} \\ & -\{f(i-1, j-1)+2 f(i-1, j)+f(i-1, j+1)\} \\ p_y= & \{f(i-1, j+1)+2 f(i, j+1)+f(i+1, j+1)\} \\ & -\{f(i-1, j-1)+2 f(i, j-1)+f(i+1, j-1)\} \end{aligned} px=py={
f(i+1,j−1)+2f(i+1,j)+f(i+1,j+1)}−{
f(i−1,j−1)+2f(i−1,j)+f(i−1,j+1)}{
f(i−1,j+1)+2f(i,j+1)+f(i+1,j+1)}−{
f(i−1,j−1)+2f(i,j−1)+f(i+1,j−1)}
得出卷积模板为:
G x = ∣ − 1 0 1 − 2 0 2 − 1 0 1 ∣ G y = ∣ − 1 − 2 − 1 0 0 0 1 2 1 ∣ G_x=\left|\begin{array}{ccc} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{array}\right| \quad G_y=\left|\begin{array}{ccc} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{array}\right| Gx=
−1−2−1000121
Gy=
−101−202−101
记图像 M \mathrm{M} M, 梯度幅值 T \mathrm{T} T, 比较
T = ( M ⊗ G x ) 2 + ( M ⊗ G y ) 2 > threshold T=\left(M \otimes G_x\right)^2+\left(M \otimes G_y\right)^2>\text { threshold } T=(M⊗Gx)2+(M⊗Gy)2> threshold
如果最终 T \mathrm{T} T 大于阈值 threshold,那么该点为边缘点。
4.3 Sobel算法优缺点
- 优点
- 一是高频的像素点少,低频的像素点多,使像素的灰度平均值下降且,由于噪声一般为高频信号,所以它具有抑制噪声的能力;
- 二是检测到的边缘比较宽,至少具有两个像素的边缘宽度
- 缺点
- 不能完全排除检测结果中出现的虚假边缘。
4.4 *Sobel**的变种——**Istropic Sobel
Sobel 算子还有一种变种 Istropic Sobel,是各向同性 Sobel 算子,其模板为
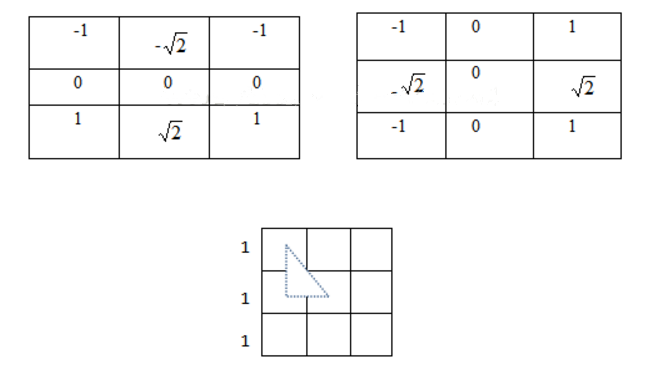
-
Sobel 各向同性算子的权值比普通 Sobel 算子的权值更准确。
-
模板的权值是离中心位置越远则权值(看绝对值)影响越小,如上图,把模板看成是 9 个小正方形,小正方 形边长为 1,则虚线三角形的斜边长为√2,下直角边长为 1,则如果(0,0)位置权值绝对值 大小为 1,则按照距离关系,位置(1,0)处的权值绝对值大小应该为√2才是准确的 。
4.5 Sobel的实现
#include "imgFeat.h"
double feat::getSobelEdge(const Mat& imgSrc, Mat& imgDst, double thresh, int direction)
{
cv::Mat gray;
// 灰度图转换
if (imgSrc.channels() == 3)
{
cv::cvtColor(imgSrc, gray, cv::COLOR_BGR2GRAY);
}
else
{
gray = imgSrc.clone();
}
int kx=0;
int ky=0;
if (direction == SOBEL_HORZ){
kx = 0; ky = 1;
}
else if (direction == SOBEL_VERT){
kx = 1; ky = 0;
}
else{
kx = 1; ky = 1;
}
// mask 卷积模板
float mask[3][3] = { { 1, 2, 1 }, { 0, 0, 0 }, { -1, -2, -1 } };
cv::Mat y_mask = Mat(3, 3, CV_32F, mask) / 8;
cv::Mat x_mask = y_mask.t(); //
//
cv::Mat sobelX, sobelY;
filter2D(gray, sobelX, CV_32F, x_mask);
filter2D(gray, sobelY, CV_32F, y_mask);
sobelX = abs(sobelX);
sobelY = abs(sobelY);
// 计算梯度
cv::Mat gradient = kx*sobelX.mul(sobelX) + ky*sobelY.mul(sobelY);
//
int scale = 4;
double cutoff;
// 阈值计算
if (thresh = -1)
{
cutoff = scale*mean(gradient)[0];
thresh = sqrt(cutoff);
}
else
{
cutoff = thresh * thresh;
}
imgDst.create(gray.size(), gray.type());
imgDst.setTo(0);
for (int i = 1; i<gray.rows - 1; i++)
{
// 数组指针
float* sbxPtr = sobelX.ptr<float>(i);
float* sbyPtr = sobelY.ptr<float>(i);
float* prePtr = gradient.ptr<float>(i - 1);
float* curPtr = gradient.ptr<float>(i);
float* lstPtr = gradient.ptr<float>(i + 1);
uchar* rstPtr = imgDst.ptr<uchar>(i);
//
for (int j = 1; j<gray.cols - 1; j++)
{
if (curPtr[j]>cutoff && ((sbxPtr[j]>kx*sbyPtr[j] && curPtr[j]>curPtr[j - 1] && curPtr[j]>curPtr[j + 1]) ||(sbyPtr[j]>ky*sbxPtr[j] && curPtr[j]>prePtr[j] && curPtr[j]>lstPtr[j])))
{
rstPtr[j] = 255;
}
}
}
return thresh;
}

5. Kirsch 算子
5.1 Kirsch算法思想
-
3*3 的卷积模板事实上涵盖着 8 种方向(左上,正上,……,右下)
-
采用 8 个 3*3 的模板对图像进行卷积,这 8 个模板代表 8 个方向,并取最大值作为 图像的边缘输出。
5.2 Kirsch算法步骤
它采用下述 8 个模板对图像上的每一个像素点进行卷积求导数:
K N = [ 5 5 5 − 3 0 3 − 3 − 3 − 3 ] , K M B = [ − 3 5 5 − 3 0 5 − 3 − 3 − 3 ] K B = [ − 3 − 3 5 − 3 0 5 − 3 − 3 5 ] , K S B = [ − 3 − 3 − 3 − 3 0 5 − 3 5 5 ] K S = [ − 3 − 3 − 3 − 3 0 − 3 5 5 5 ] , K S W = [ − 3 − 3 − 3 5 0 − 3 5 5 − 3 ] K W = [ 5 − 3 − 3 5 0 − 3 5 − 3 − 3 ] , K N W = [ 5 5 − 3 5 0 − 3 − 3 − 3 − 3 ] \begin{aligned} & K_N=\left[\begin{array}{ccc} 5 & 5 & 5 \\ -3 & 0 & 3 \\ -3 & -3 & -3 \end{array}\right], \mathrm{K}_{M B}=\left[\begin{array}{ccc} -3 & 5 & 5 \\ -3 & 0 & 5 \\ -3 & -3 & -3 \end{array}\right] \\ & K_B=\left[\begin{array}{ccc} -3 & -3 & 5 \\ -3 & 0 & 5 \\ -3 & -3 & 5 \end{array}\right], \mathrm{K}_{S B}=\left[\begin{array}{ccc} -3 & -3 & -3 \\ -3 & 0 & 5 \\ -3 & 5 & 5 \end{array}\right] \\ & K_S=\left[\begin{array}{ccc} -3 & -3 & -3 \\ -3 & 0 & -3 \\ 5 & 5 & 5 \end{array}\right], \mathrm{K}_{S W}=\left[\begin{array}{ccc} -3 & -3 & -3 \\ 5 & 0 & -3 \\ 5 & 5 & -3 \end{array}\right] \\ & K_W=\left[\begin{array}{ccc} 5 & -3 & -3 \\ 5 & 0 & -3 \\ 5 & -3 & -3 \end{array}\right], \mathrm{K}_{N W}=\left[\begin{array}{ccc} 5 & 5 & -3 \\ 5 & 0 & -3 \\ -3 & -3 & -3 \end{array}\right] \end{aligned} KN=
5−3−350−353−3
,KMB=
−3−3−350−355−3
KB=
−3−3−3−30−3555
,KSB=
−3−3−3−305−355
KS=
−3−35−305−3−35
,KSW=
−355−305−3−3−3
KW=
555−30−3−3−3−3
,KNW=
55−350−3−3−3−3
最终选取 8 次卷积结果的最大值作为图像的边缘输出。
5.3 Kirsch算法计算优化
假设图像中一点 A 及其周围 3×3 区域的灰度如下图所示,设 q i ( i = 0 , 1 , 2...7 ) q_i(i=0,1,2...7) qi(i=0,1,2...7)为图像 经过 Kirsch 算子第 i + 1 i+1 i+1个模板处理后得到的 A 点的灰度值。
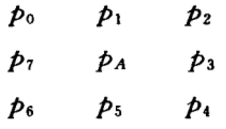
处理后在 A 点的灰度值为:
q i = m a x { q i } ( i = 0 , 1 , 2...7 ) q_i=max\left\{q_i\right\} (i=0,1,2...7) qi=max{
qi}(i=0,1,2...7)
通过矩阵变换发现经过 Kirsch 算子得到的像素值直接的关系, 事实上需要直接由邻域 像素点计算得到的只有 p 0 p_0 p0, , 因此可以大大减少计算量。
Q = 1 / 8 ( q 0 , q 1 , ⋯ , q 1 ) T = ( r 0 , r 1 , ⋯ , r 7 ) T r 0 = 0.625 ( p 0 + p 1 + p 2 ) − 0.375 ( p 3 + p 4 + p 5 + p 6 + p 7 ) r 1 = r 0 + p 7 − p 2 r 2 = r 1 + p 6 − p 1 r 3 = r 2 + p 5 − p 0 r 4 = r 3 + p 4 − p 7 r 5 = r 4 + p 3 − p 6 r 6 = r 5 + p 2 − p 5 r 7 = r 6 + p 1 − p 4 q A = max { q i } = 8 max { r i } ( i = 0 , 1 , ⋯ , 7 ) \begin{aligned} & Q=1 / 8\left(q_0, q_1, \cdots, q_1\right)^T=\left(r_0, r_1, \cdots, r_7\right)^{\mathrm{T}} \\ & r_0=0.625\left(p_0+p_1+p_2\right)-0.375\left(p_3+p_4+p_5+p_6+p_7\right) \\ & r_1=r_0+p_7-p_2 \quad r_2=r_1+p_6-p_1 \quad r_3=r_2+p_5-p_0 \\ & r_4=r_3+p_4-p_7 \quad r_5=r_4+p_3-p_6 \quad r_6=r_5+p_2-p_5 \\ & r_7=r_6+p_1-p_4 \\ & \mathrm{q}_{\mathrm{A}}=\max \left\{\mathrm{q}_{\mathrm{i}}\right\}=8 \max \left\{\mathbf{r}_{\mathrm{i}}\right\} \quad(\mathrm{i}=0,1, \cdots, 7) \\ & \end{aligned} Q=1/8(q0,q1,⋯,q1)T=(r0,r1,⋯,r7)Tr0=0.625(p0+p1+p2)−0.375(p3+p4+p5+p6+p7)r1=r0+p7−p2r2=r1+p6−p1r3=r2+p5−p0r4=r3+p4−p7r5=r4+p3−p6r6=r5+p2−p5r7=r6+p1−p4qA=max{
qi}=8max{
ri}(i=0,1,⋯,7)
5.4 Kirsch算法优缺点
-
Kirsch 算子属于模板匹配算子,采用八个模板来处理图像的检测图像的边缘,运算量比较大,
-
在保持细节和抗噪声方面都有较好的效果。
5.5 *Robinson算子
Robinson 与 Kirsch 算子非常类似, 也是 8 个模板, 只是模板的内容有差异:
R N = [ 1 2 1 0 0 0 − 1 − 2 1 ] , R H B = [ 0 1 2 − 1 0 1 − 2 − 1 0 ] R B = [ − 1 0 1 − 2 0 2 − 1 0 1 ] , R S B = [ − 2 − 1 0 − 1 0 1 0 1 2 ] R S = [ − 1 − 2 − 1 0 0 0 1 2 1 ] , R S W = [ 0 − 1 − 2 1 0 − 1 2 1 0 ] R W = [ 1 0 − 1 2 0 − 2 1 0 − 1 ] , R N W = [ 2 1 0 1 0 − 1 0 − 1 − 2 ] \begin{aligned} R_N & =\left[\begin{array}{ccc} 1 & 2 & 1 \\ 0 & 0 & 0 \\ -1 & -2 & 1 \end{array}\right], \mathrm{R}_{H B}=\left[\begin{array}{ccc} 0 & 1 & 2 \\ -1 & 0 & 1 \\ -2 & -1 & 0 \end{array}\right] \\ R_B & =\left[\begin{array}{lll} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{array}\right], \mathrm{R}_{S B}=\left[\begin{array}{ccc} -2 & -1 & 0 \\ -1 & 0 & 1 \\ 0 & 1 & 2 \end{array}\right] \\ R_S & =\left[\begin{array}{ccc} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{array}\right], \mathrm{R}_{S W}=\left[\begin{array}{ccc} 0 & -1 & -2 \\ 1 & 0 & -1 \\ 2 & 1 & 0 \end{array}\right] \\ R_W & =\left[\begin{array}{lll} 1 & 0 & -1 \\ 2 & 0 & -2 \\ 1 & 0 & -1 \end{array}\right], \mathrm{R}_{N W}=\left[\begin{array}{ccc} 2 & 1 & 0 \\ 1 & 0 & -1 \\ 0 & -1 & -2 \end{array}\right] \end{aligned} RNRBRSRW=
10−120−2101
,RHB=
0−1−210−1210
=
−1−2−1000121
,RSB=
−2−10−101012
=
−101−202−101
,RSW=
012−101−2−10
=
121000−1−2−1
,RNW=
21010−10−1−2
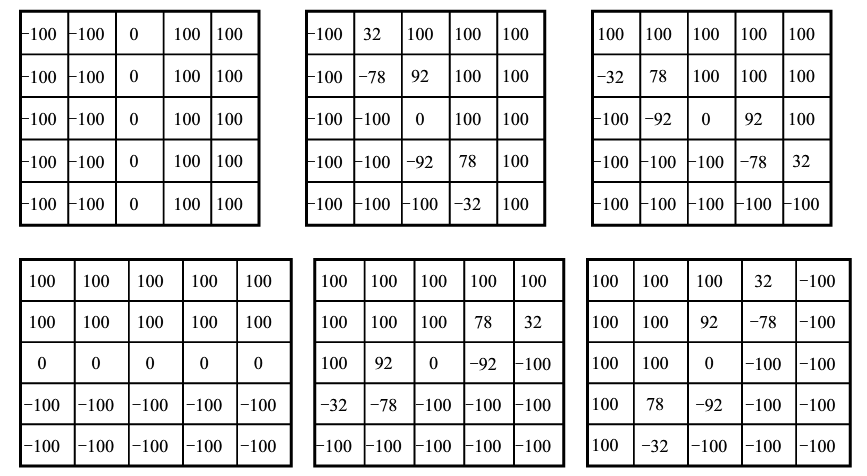
6. *Nevitia 算子
evitia 算子采用的是 5×5 的卷积模板,它与 Kirsch 类似,也是属于方向算子,总共 能确定 4*(5-1)=12 个方向,因此包含有 12 个 5×5 的模板。 其中前 6 个模板如下,后 6 个模板可以由对称性得到。 最终选取 12 次卷积结果的最大值作为图像的边缘输出。
第三章 二阶微分边缘算子
1. 二阶微分边缘算子基本思想
-
边缘即是图像的一阶导数局部最大值的地方,那么也意味着 该点的二阶导数为零。二阶微分边缘检测算子就是利用图像在边缘处的阶跃性导致图像二 阶微分在边缘处出现零值这一特性进行边缘检测的。
-
对于图像的二阶微分可以用拉普拉斯算子来表示:
∇ 2 I = ∂ 2 I ∂ x 2 + ∂ 2 I ∂ y 2 \nabla^2 I=\frac{\partial^2 I}{\partial x^2}+\frac{\partial^2 I}{\partial y^2} ∇2I=∂x2∂2I+∂y2∂2I
我们在像素点 ( i , j ) (\mathrm{i}, \mathrm{j}) (i,j) 的 3 × 3 3 \times 3 3×3 的邻域内, 可以有如下的近似:
∂ 2 I ∂ x 2 = I ( i , j + 1 ) − 2 I ( i , j ) + I ( i , j − 1 ) ∂ 2 I ∂ y 2 = I ( i + 1 , j ) − 2 I ( i , j ) + I ( i − 1 , j ) ∇ 2 I = − 4 I ( i , j ) + I ( i , j + 1 ) + I ( i , j − 1 ) + I ( i + 1 , j ) + I ( i − 1 , j ) \begin{gathered} \frac{\partial^2 I}{\partial x^2}=I(i, j+1)-2 I(i, j)+I(i, j-1) \\ \frac{\partial^2 I}{\partial y^2}=I(i+1, j)-2 I(i, j)+I(i-1, j) \\ \nabla^2 I=-4 I(i, j)+I(i, j+1)+I(i, j-1)+I(i+1, j)+I(i-1, j) \end{gathered} ∂x2∂2I=I(i,j+1)−2I(i,j)+I(i,j−1)∂y2∂2I=I(i+1,j)−2I(i,j)+I(i−1,j)∇2I=−4I(i,j)+I(i,j+1)+I(i,j−1)+I(i+1,j)+I(i−1,j)
对应的二阶微分卷积核为:
m = [ 0 1 0 1 4 1 0 1 0 ] \boldsymbol{m}=\left[\begin{array}{lll} 0 & 1 & 0 \\ 1 & 4 & 1 \\ 0 & 1 & 0 \end{array}\right] m=
010141010
所以二阶微分检测边缘的方法就分两步:
- 用上面的 Laplace 核与图像进行卷积;
- 对卷积后的图像, 取得那些卷积结果为 0 的点。
2. Laplace 算子
2.1 拉普拉斯表达式
Laplace (拉普拉斯) 算子是最简单的各向同性微分算子, 一个二维图像函数的拉普拉 斯变换是各向同性的二阶导数。
Laplace 算子的表达式:
∇ 2 f ( x , y ) = ∂ 2 f ( x , y ) ∂ x 2 + ∂ 2 f ( x , y ) ∂ y 2 \nabla^2 f(x, y)=\frac{\partial^2 f(x, y)}{\partial x^2}+\frac{\partial^2 f(x, y)}{\partial y^2} ∇2f(x,y)=∂x2∂2f(x,y)+∂y2∂2f(x,y)
我们知道梯度的表达式为 ∇ = ∂ ∂ x i ⃗ + ∂ ∂ y j ⃗ \nabla=\frac{\partial}{\partial x} \vec{i}+\frac{\partial}{\partial y} \vec{j} ∇=∂x∂i+∂y∂j, 于是上式的推导过程就是:
∇ 2 ≜ ∇ ⋅ ∇ = ( ∂ ∂ x i ⃗ + ∂ ∂ y j ⃗ ) ⋅ ( ∂ ∂ x i ⃗ + ∂ ∂ y j ⃗ ) = ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 \nabla^2 \triangleq \nabla \cdot \nabla=\left(\frac{\partial}{\partial x} \vec{i}+\frac{\partial}{\partial y} \vec{j}\right) \cdot\left(\frac{\partial}{\partial x} \vec{i}+\frac{\partial}{\partial y} \vec{j}\right)=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2} ∇2≜∇⋅∇=(∂x∂i+∂y∂j)⋅(∂x∂i+∂y∂j)=∂x2∂2+∂y2∂2
2.2 图像中的Laplace算子
考虑到图像是离散的二维矩阵, 用差分近似微分可以得到:
∂ 2 f ∂ x 2 = ∂ G ∂ x = ∂ [ f ( i , j ) − f ( i , j − 1 ) ] ∂ x = ∂ f ( i , j ) ∂ x − ∂ f ( i , j − 1 ) ∂ x = [ f ( i , j + 1 ) − f ( i , j ) ] − [ f ( i , j ) − f ( i , j − 1 ) ] = f ( i , j + 1 ) − 2 f ( i , j ) + f ( i , j − 1 ) \begin{aligned} & \frac{\partial^2 f}{\partial x^2}=\frac{\partial G}{\partial x}=\frac{\partial[\mathrm{f}(\mathbf{i}, \mathrm{j})-\mathrm{f}(\mathrm{i}, \mathrm{j}-1)]}{\partial x}=\frac{\partial \mathrm{f}(\mathrm{i}, \mathrm{j})}{\partial x}-\frac{\partial \mathrm{f}(\mathrm{i}, \mathrm{j}-1)}{\partial x} \\ & =[f(i, j+1)-f(i, j)]-[f(i, j)-f(i, j-1)] \\ & =f(i, j+1)-2 f(i, j)+f(i, j-1) \\ & \end{aligned} ∂x2∂2f=∂x∂G=∂x∂[f(i,j)−f(i,j−1)]=∂x∂f(i,j)−∂x∂f(i,j−1)=[f(i,j+1)−f(i,j)]−[f(i,j)−f(i,j−1)]=f(i,j+1)−2f(i,j)+f(i,j−1)
同理, 可得:
∂ f 2 ∂ x 2 = f ( i + 1 , j ) − 2 f ( i , j ) + f ( i − 1 , j ) \frac{\partial_f^2}{\partial x^2}=f(i+1, j)-2 f(i, j)+f(i-1, j) ∂x2∂f2=f(i+1,j)−2f(i,j)+f(i−1,j)
于是有:
∇ 2 f = ∂ f 2 ∂ x 2 + ∂ f 2 ∂ x 2 = f ( i + 1 , j ) + f ( i − 1 , j ) + f ( i , j + 1 ) + f ( i , j − 1 ) − 4 f ( i , j ) \nabla^2 \mathrm{f}=\frac{\partial_f^2}{\partial x^2}+\frac{\partial_f^2}{\partial x^2}=f(i+1, j)+f(i-1, j)+f(i, j+1)+f(i, j-1)-4 f(i, j) ∇2f=∂x2∂f2+∂x2∂f2=f(i+1,j)+f(i−1,j)+f(i,j+1)+f(i,j−1)−4f(i,j)
用模板来表示为:
[ 0 1 0 1 − 4 1 0 1 0 ] \left[\begin{array}{ccc} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{array}\right]
0101−41010
还有一种常用的卷积模板为:
[ − 1 − 1 − 1 − 1 8 − 1 − 1 − 1 − 1 ] \left[\begin{array}{ccc} -1 & -1 & -1 \\ -1 & 8 & -1 \\ -1 & -1 & -1 \end{array}\right]
−1−1−1−18−1−1−1−1
有时我们为了在邻域中心位置取到更大的权值,还使用如下卷积模板:
[ 1 4 1 4 − 20 1 1 4 1 ] \left[\begin{array}{ccc} 1 & 4 & 1 \\ 4 & -20 & 1 \\ 1 & 4 & 1 \end{array}\right]
1414−204111
2.3 Laplace算法过程
-
遍历图像(除去边缘,防止越界),对每个像素做Laplancian模板卷积运算,注意是只做其中的一种模板运算,并不是两个。
-
复制到目标图像,结束。
2.4 Laplace算子的旋转不变性证明
∇ 2 f = ∂ 2 f ∂ x ′ 2 + ∂ 2 f ∂ y ′ 2 = ∂ ∂ x ′ ( ∂ f ∂ x ′ ) + ∂ ∂ y ′ ( ∂ f ∂ y ′ ) = ∂ ∂ x ′ ( ∂ f ∂ x ∂ x ∂ x ′ + ∂ f ∂ y ∂ y ∂ x ′ ) + ∂ ∂ y ′ ( ∂ f ∂ x ∂ x ∂ y ′ + ∂ f ∂ y ∂ y ∂ y ′ ) = ∂ ∂ x ′ ( ∂ f ∂ x cos θ + ∂ f ∂ y sin θ ) + ∂ ∂ y ′ ( − sin θ ∂ f ∂ x + cos θ ∂ f ∂ y ) = ∂ ∂ x ( ∂ f ∂ x cos θ + ∂ f ∂ y sin θ ) ∂ x ∂ x ′ + ∂ ∂ y ( ∂ f ∂ x cos θ + ∂ f ∂ y sin θ ) ∂ y ∂ x ′ + ∂ ∂ x ( − sin θ ∂ f ∂ x + cos ∂ f ∂ y ) ∂ x ∂ y ′ + ∂ ∂ y ( − sin θ ∂ f ∂ x + cos ∂ f ∂ y ) ∂ y ∂ y ′ ∂ ∂ x ( ∂ f ∂ x cos θ + ∂ f ∂ y sin θ ) cos θ + ∂ ∂ y ( ∂ f ∂ x cos θ + ∂ f ∂ y sin θ ) sin θ + ∂ ∂ x ( − sin θ ∂ f ∂ x + cos ∂ f ∂ y ) ( − sin θ ) + ∂ ∂ y ( − sin θ ∂ f ∂ x + cos θ ∂ f ∂ y ) cos θ = ∂ ∂ x ∂ f ∂ x + ∂ ∂ y ∂ f ∂ y = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 \begin{aligned} \nabla^2 f & =\frac{\partial^2 f}{\partial x^{\prime 2}}+\frac{\partial^2 f}{\partial y^{\prime 2}} \\ & =\frac{\partial}{\partial x^{\prime}}\left(\frac{\partial f}{\partial x^{\prime}}\right)+\frac{\partial}{\partial y^{\prime}}\left(\frac{\partial f}{\partial y^{\prime}}\right) \\ = & \frac{\partial}{\partial x^{\prime}}\left(\frac{\partial f}{\partial x} \frac{\partial x}{\partial x^{\prime}}+\frac{\partial f}{\partial y} \frac{\partial y}{\partial x^{\prime}}\right)+\frac{\partial}{\partial y^{\prime}}\left(\frac{\partial f}{\partial x} \frac{\partial x}{\partial y^{\prime}}+\frac{\partial f}{\partial y} \frac{\partial y}{\partial y^{\prime}}\right) \\ = & \frac{\partial}{\partial x^{\prime}}\left(\frac{\partial f}{\partial x} \cos \theta+\frac{\partial f}{\partial y} \sin \theta\right)+\frac{\partial}{\partial y^{\prime}}\left(-\sin \theta \frac{\partial f}{\partial x}+\cos \theta \frac{\partial f}{\partial y}\right) \\ = & \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x} \cos \theta+\frac{\partial f}{\partial y} \sin \theta\right) \frac{\partial x}{\partial x^{\prime}}+\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x} \cos \theta+\frac{\partial f}{\partial y} \sin \theta\right) \frac{\partial y}{\partial x^{\prime}} \\ & \quad+\frac{\partial}{\partial x}\left(-\sin \theta \frac{\partial f}{\partial x}+\cos \frac{\partial f}{\partial y}\right) \frac{\partial x}{\partial y^{\prime}}+\frac{\partial}{\partial y}\left(-\sin \theta \frac{\partial f}{\partial x}+\cos \frac{\partial f}{\partial y}\right) \frac{\partial y}{\partial y^{\prime}} \\ & \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x} \cos \theta+\frac{\partial f}{\partial y} \sin \theta\right) \cos \theta+\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x} \cos \theta+\frac{\partial f}{\partial y} \sin \theta\right) \sin \theta \\ & \quad+\frac{\partial}{\partial x}\left(-\sin \theta \frac{\partial f}{\partial x}+\cos \frac{\partial f}{\partial y}\right)(-\sin \theta)+\frac{\partial}{\partial y}\left(-\sin \theta \frac{\partial f}{\partial x}+\cos \theta \frac{\partial f}{\partial y}\right) \cos \theta \\ = & \frac{\partial}{\partial x} \frac{\partial f}{\partial x}+\frac{\partial}{\partial y} \frac{\partial f}{\partial y} \\ = & \frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2} \end{aligned} ∇2f======∂x′2∂2f+∂y′2∂2f=∂x′∂(∂x′∂f)+∂y′∂(∂y′∂f)∂x′∂(∂x∂f∂x′∂x+∂y∂f∂x′∂y)+∂y′∂(∂x∂f∂y′∂x+∂y∂f∂y′∂y)∂x′∂(∂x∂fcosθ+∂y∂fsinθ)+∂y′∂(−sinθ∂x∂f+cosθ∂y∂f)∂x∂(∂x∂fcosθ+∂y∂fsinθ)∂x′∂x+∂y∂(∂x∂fcosθ+∂y∂fsinθ)∂x′∂y+∂x∂(−sinθ∂x∂f+cos∂y∂f)∂y′∂x+∂y∂(−sinθ∂x∂f+cos∂y∂f)∂y′∂y∂x∂(∂x∂fcosθ+∂y∂fsinθ)cosθ+∂y∂(∂x∂fcosθ+∂y∂fsinθ)sinθ+∂x∂(−sinθ∂x∂f+cos∂y∂f)(−sinθ)+∂y∂(−sinθ∂x∂f+cosθ∂y∂f)cosθ∂x∂∂x∂f+∂y∂∂y∂f∂x2∂2f+∂y2∂2f
2.4 Laplace算子优缺点
Laplace 算子具有旋转不变性,适用于仅注重边缘点所处的具体位置,而对边缘点附近的实际灰度差没有要求的情况。不过在边缘检测中并不常用拉普拉斯算子,而主要是用在判断像素是在边缘亮的一面还是暗的一面,主要有以下三点原因:
-
二阶导数算子与一阶导数算子相比,去除噪声的能力更弱;
-
该算子对边缘的方向检测不到;
-
该算子的幅值会产生双边元。
为了使图像的抗噪能力提高,人们提出了下节将要介绍的改进的 LOG(Laplacian of Gaussian) 算子。
3. LOG 算子
3.1 LoG算子概述
- 先运用高斯滤波器平滑图像达到去除噪声的目的,然后用 Laplace 算子对图 像边缘进行检测。
- 这样既达到了降低噪声的效果,同时也使边缘平滑,并得到了延展。为了 防止得到不必要的边缘,边缘点应该选取比某阈值高的一阶导数零交叉点。
- LOG 算子已经 成为目前对阶跃边缘用二阶导数过零点来检测的最好的算子。
3.2 LoG解决的问题
直接使用 Laplace 算法,去噪的能力是非常弱的,最终提取出的边缘信息 极易被噪音干扰,如下图所示:
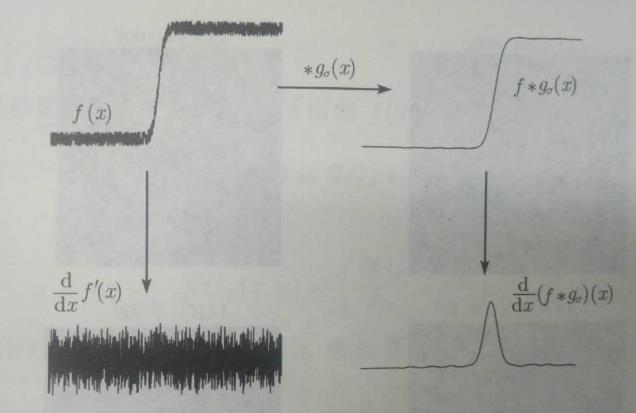
LoG 解决的最重要的问题是在提取边缘信息之前给原始图像增添一层高斯滤波器,使得原始图像的梯度异常点大大减少,最终能够更有效地提取出边缘信息。
3.3 LoG算子的计算过程
在图像处理中,常用的二维高斯函数为 :
G ( x , y , σ ) = 1 2 π σ 2 e − ( x 2 + y 2 ) / 2 σ 2 G(x, y, \sigma)=\frac{1}{2 \pi \sigma^2} e^{-\left(x^2+y^2\right) / 2 \sigma^2} G(x,y,σ)=2πσ21e−(x2+y2)/2σ2
拉普拉斯算子为
∇ 2 f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 \nabla^2 f=\frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2} ∇2f=∂x2∂2f+∂y2∂2f
对二维高斯函数应用拉普拉斯算子得
∇ 2 G = ∂ 2 G ∂ x 2 + ∂ 2 G ∂ y 2 = − 2 σ 2 + x 2 + y 2 2 π σ 6 e − ( x 2 + y 2 ) / 2 σ 2 \nabla^2 G=\frac{\partial^2 G}{\partial x^2}+\frac{\partial^2 G}{\partial y^2}=\frac{-2 \sigma^2+x^2+y^2}{2 \pi \sigma^6} e^{-\left(x^2+y^2\right) / 2 \sigma^2} ∇2G=∂x2∂2G+∂y2∂2G=2πσ6−2σ2+x2+y2e−(x2+y2)/2σ2
LoG (Laplacian of Gaussian) 算子定义为
L o G = σ 2 ∇ 2 G L o G=\sigma^2 \nabla^2 G LoG=σ2∇2G
注意到 LoG 算子, 该函数轴对称, 且函数的平均值为 o \mathrm{o} o (在定义域内), 所以用它与图像进行卷积计算并不会对完整的图像动态区域有所改变, 而是会使图像模糊(因为它相当 平滑), 且模糊程度与 σ \sigma σ 成正比。
- 当 σ \sigma σ 较大时, 高斯滤波起到了很好的平滑效果, 较大程度地抑制了噪声, 但同时使一些边缘细节丢失, 降低了图像边缘的定位精度;
- 当 σ \sigma σ 比较小时, 有很强的图像边缘定位精度, 反而信噪比较低。
- 在应用 LOG 算子时, 如何选取适当的 σ \sigma σ 值很重要, 要根据边缘的定位精度的需求以及噪声情况而定。
3.4 LoG的卷积模板
LOG 算子的卷积模板通常采用 5×5 的矩阵,如:

计算代码流程:

其中左边这个模板是在高斯标准差为 0.5 时的逼近,右边的模板的高斯标准差为 1。
Normalize 是一个正则函数,它确保模板系数的总和为 1. 以便在均匀亮度区域不会检测到 边缘。最后由于整数比浮点数更易于计算,模板的系数都会近似为整数。
3.5 LoG算法过程
(1)遍历图像(除去边缘,防止越界),对每个像素做 Gauss -Laplancian 模板卷积运 算。
(2)复制到目标图像,结束。
3.6 DoG与LoG
简化 LOG 的计算——这便是 DOG 算子。 DoG(Difference of Gaussian)算子定义为 :
D o G = G ( x , y , σ 1 ) − G ( x , y , σ 2 ) D o G=G\left(x, y, \sigma_1\right)-G\left(x, y, \sigma_2\right) DoG=G(x,y,σ1)−G(x,y,σ2)
下面我们来证明为何 DoG 能近似替代 LoG。
对二维高斯函数关于 σ \sigma σ 求一阶偏导数得
∂ G ∂ σ = − 2 σ 2 + x 2 + y 2 2 π σ 5 e − ( x 2 + y 2 ) / 2 σ 2 \frac{\partial G}{\partial \sigma}=\frac{-2 \sigma^2+x^2+y^2}{2 \pi \sigma^5} e^{-\left(x^2+y^2\right) / 2 \sigma^2} ∂σ∂G=2πσ5−2σ2+x2+y2e−(x2+y2)/2σ2
不难发现
∂ G ∂ σ = σ ∇ 2 G \frac{\partial G}{\partial \sigma}=\sigma \nabla^2 G ∂σ∂G=σ∇2G
在 DoG 算子中, 令 σ 1 = k σ 2 = k σ \sigma 1=\mathrm{k} \sigma 2=\mathrm{k \sigma} σ1=kσ2=kσ, 则
D o G = G ( x , y , k σ ) − G ( x , y , σ ) D o G=G(x, y, k \sigma)-G(x, y, \sigma) DoG=G(x,y,kσ)−G(x,y,σ)
进一步地
∂ G ∂ σ = lim Δ σ → 0 G ( x , y , σ + Δ σ ) − G ( x , y , σ ) ( σ + Δ σ ) − σ ≈ G ( x , y , k σ ) − G ( x , y , σ ) k σ − σ \frac{\partial G}{\partial \sigma}=\lim _{\Delta \sigma \rightarrow 0} \frac{G(x, y, \sigma+\Delta \sigma)-G(x, y, \sigma)}{(\sigma+\Delta \sigma)-\sigma} \approx \frac{G(x, y, k \sigma)-G(x, y, \sigma)}{k \sigma-\sigma} ∂σ∂G=Δσ→0lim(σ+Δσ)−σG(x,y,σ+Δσ)−G(x,y,σ)≈kσ−σG(x,y,kσ)−G(x,y,σ)
因此
σ ∇ 2 G = ∂ G ∂ σ ≈ G ( x , y , k σ ) − G ( x , y , σ ) k σ − σ \sigma \nabla^2 G=\frac{\partial G}{\partial \sigma} \approx \frac{G(x, y, k \sigma)-G(x, y, \sigma)}{k \sigma-\sigma} σ∇2G=∂σ∂G≈kσ−σG(x,y,kσ)−G(x,y,σ)
即
G ( x , y , k σ ) − G ( x , y , σ ) ≈ ( k − 1 ) σ 2 ∇ 2 G G(x, y, k \sigma)-G(x, y, \sigma) \approx(k-1) \sigma^2 \nabla^2 G G(x,y,kσ)−G(x,y,σ)≈(k−1)σ2∇2G
这表明 DoG 算子可以近似于 LoG 算子, 证毕。
于是, 使用 DoG 算子, 让我们只需对图像进行两次高斯平滑再将结果相减就可以近似 得到 LOG 作用于图像的效果了。
值得注意的是, 当我们用 DOG 算子代替 LOG 算子与图像卷积的时候:
DoG ( x , y , σ 1 , σ 2 ) ∗ I ( x , y ) = G ( x , y , σ 1 ) ∗ I ( x , y ) − G ( x , y , σ 2 ) ∗ I ( x , y ) \operatorname{DoG}\left(x, y, \sigma_1, \sigma_2\right) * I(x, y)=G\left(x, y, \sigma_1\right) * I(x, y)-G\left(x, y, \sigma_2\right) * I(x, y) DoG(x,y,σ1,σ2)∗I(x,y)=G(x,y,σ1)∗I(x,y)−G(x,y,σ2)∗I(x,y)
近似的 LOG 算子值的选取:
σ 2 = σ 1 2 σ 2 2 σ 1 2 − σ 2 2 ln [ σ 1 2 σ 2 2 ] \sigma^2=\frac{\sigma_1^2 \sigma_2^2}{\sigma_1^2-\sigma_2^2} \ln \left[\frac{\sigma_1^2}{\sigma_2^2}\right] σ2=σ12−σ22σ12σ22ln[σ22σ12]
当使用这个值时, 可以保证 LoG 和 DoG 的过零点相同, 只是幅度大小不同。
3.7 LoG算子优缺点
- 优点
- LoG 这种方法寻找二阶导数是很稳定的。
- 高斯平滑有效地抑制了距离当前像素 3σ 范围内的所有像素的影响,这样 Laplace 算子就构成了一种反映图像变化的有效 而稳定的度量。
- 传统的二阶导数过零点技术也有缺点。
- 第一,对形状作了过分的平滑。
- 第二, 它有产生环形边缘的倾向。
4. Canny 算子
4.1 Canny算子概述
- 基于图像梯度计算的边缘检测算法
- Canny 根据以前的边缘检测算子以及应用,归纳了如下三条准则:
- 信噪比准则:避免真实的边缘丢失,避免把非边缘点错判为边缘点;
- 定位精度准则:得到的边缘要尽量与真实边缘接近;
- 单一边缘响应准则:单一边缘需要具有独一无二的响应,要避免出现多个响应,并最大抑制虚假响应。
以上三条准则是由 Canny 首次明确提出并对这个问题进行完全解决的,虽然在他之前有人提出过类似的要求。更为重要的是, Canny 同时给出了它们的数学表达式(现以一维为例),这就转化成为一个泛函优化的问题 。
4.2 Canny算子检测步骤
经典的 Canny 边缘检测算法通常都是从高斯模糊开始,到基于双阈值实现边缘连接结束。但是在实际工程应用中,考虑到输入图像都是彩色图像,最终边缘连接之后的图像要二值化输出显示,所以完整的 Canny 边缘检测算法实现步骤如下:
- 彩色图像转换为灰度图像
- 对图像进行高斯模糊
- 计算图像梯度,根据梯度计算图像边缘幅值与角度
- 非极大值抑制(边缘细化)
- 双阈值检测
- 通过抑制孤立的弱边缘完成边缘检测
- 二值化图像输出结果
4.3 Canny算子各步骤详解
-
彩色图像转换为灰度图像
根据彩色图像 RGB 转灰度公式: g r a y = R ∗ 0.299 + G ∗ 0.587 + B ∗ 0.114 gray = R * 0.299 + G * 0.587 + B * 0.114 gray=R∗0.299+G∗0.587+B∗0.114
-
对图像进行高斯模糊
为了尽可能减少噪声对边缘检测结果的影响,所以必须滤除噪声以防止由噪声引起的错 误检测。为了平滑图像,使用高斯滤波器与图像进行卷积,该步骤将平滑图像,以减少边缘 检测器上明显的噪声影响。大小为 ( 2 k + 1 ) ∗ ( 2 k + 1 ) (2k+1)*(2k+1) (2k+1)∗(2k+1)的高斯滤波器核的生成方程式由下式给出:
H i j = 1 2 π σ 2 exp ( − ( i − ( k + 1 ) ) 2 + ( j − ( k + 1 ) ) 2 2 σ 2 ) ; 1 ≤ i , j ≤ ( 2 k + 1 ) ( 3 − 1 ) H_{i j}=\frac{1}{2 \pi \sigma^2} \exp \left(-\frac{(i-(k+1))^2+(j-(k+1))^2}{2 \sigma^2}\right) ; 1 \leq i, j \leq(2 k+1) \quad(3-1) Hij=2πσ21exp(−2σ2(i−(k+1))2+(j−(k+1))2);1≤i,j≤(2k+1)(3−1)
下面是一个 sigma = 1.4 =1.4 =1.4, 尺寸为 3 × 3 3 \times 3 3×3 的高斯卷积核的例子(需要注意归一化):
H = [ 0.0924 0.1192 0.0924 0.1192 0.1538 0.1192 0.0924 0.1192 0.0924 ] H=\left[\begin{array}{lll} 0.0924 & 0.1192 & 0.0924 \\ 0.1192 & 0.1538 & 0.1192 \\ 0.0924 & 0.1192 & 0.0924 \end{array}\right] H= 0.09240.11920.09240.11920.15380.11920.09240.11920.0924
若图像中一个 3 × 3 3 \times 3 3×3 的窗口为 A \mathrm{A} A, 要滤波的像素点为 e \mathrm{e} e, 则经过高斯滤波之后, 像素点 e \mathrm{e} e 的亮度值为:
e = H ∗ A = [ h 11 h 12 h 13 h 21 h 22 h 23 h 31 h 32 h 33 ] ∗ [ a b c d e f g h i ] = sum ( [ a × h 11 b × h 12 c × h 13 d × h 21 e × h 22 f × h 23 g × h 31 h × h 32 i × h 33 ] ) e=H * A=\left[\begin{array}{lll} \mathrm{h}_{11} & \mathrm{~h}_{12} & \mathrm{~h}_{13} \\ \mathrm{~h}_{21} & \mathrm{~h}_{22} & \mathrm{~h}_{23} \\ \mathrm{~h}_{31} & \mathrm{~h}_{32} & \mathrm{~h}_{33} \end{array}\right] *\left[\begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \end{array}\right]=\operatorname{sum}\left(\left[\begin{array}{lll} \mathrm{a} \times \mathrm{h}_{11} & \mathrm{~b} \times \mathrm{h}_{12} & \mathrm{c} \times \mathrm{h}_{13} \\ \mathrm{~d} \times \mathrm{h}_{21} & \mathrm{e} \times \mathrm{h}_{22} & \mathrm{f} \times \mathrm{h}_{23} \\ \mathrm{~g} \times \mathrm{h}_{31} & \mathrm{~h} \times \mathrm{h}_{32} & \mathrm{i} \times \mathrm{h}_{33} \end{array}\right]\right) e=H∗A= h11 h21 h31 h12 h22 h32 h13 h23 h33 ∗ adgbehcfi =sum a×h11 d×h21 g×h31 b×h12e×h22 h×h32c×h13f×h23i×h33
其中*为卷积符号, sum 表示矩阵中所有元素相加求和。
重要的是需要理解, 高斯卷积核大小的选择将影响 Canny 检测器的性能。- 尺寸越大, 检测器对噪声的敏感度越低, 但是边缘检测的定位误差也将略有增加。
- 一般 5 × 5 5 \times 5 5×5 是一个比较不错的 trade off。
-
计算图像梯度,根据梯度计算图像边缘幅值与角度
图像中的边缘可以指向各个方向, 因此 Canny 算法使用四个算子来检测图像中的水平、 垂直和对角边缘。边缘检测的算子 (如 Roberts, Prewitt, Sobel 等) 返回水平 G x \mathrm{Gx} Gx 和垂直 G y Gy Gy 方向的一阶导数值, 由此便可以确定像素点的梯度 G \mathrm{G} G 和方向 theta 。
G = G x 2 + G y 2 θ = arctan ( G y / G x ) \begin{aligned} & G=\sqrt{G_x^2+G_y^2} \\ & \theta=\arctan \left(G_y / G_x\right) \end{aligned} G=Gx2+Gy2θ=arctan(Gy/Gx)
其中 G \mathrm{G} G 为梯度强度, theta 表示梯度方向, arctan \arctan arctan 为反正切函数。 -
非极大值抑制(边缘细化)
非极大值抑制是一种边缘稀疏技术,非极大值抑制的作用在于“瘦”边。对图像进行 梯度计算后,仅仅基于梯度值提取的边缘仍然很模糊。对于标准 3,对边缘有且应当只有 一个准确的响应。而非极大值抑制则可以帮助将局部最大值之外的所有梯度值抑制为 0, 对梯度图像中每个像素进行非极大值抑制的算法是: 1) 将当前像素的梯度强度与沿正负梯度方向上的两个像素进行比较。 2) 如果当前像素的梯度强度与另外两个像素相比最大,则该像素点保留为边缘点,否 则该像素点将被抑制。
通常为了更加精确的计算,在跨越梯度方向的两个相邻像素之间使用线性插值来得到要 比较的像素梯度,现举例如下:
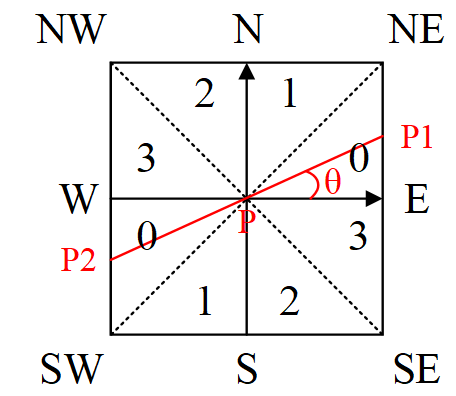
如上图所示,将梯度分为 8 个方向,分别为 E、NE、N、NW、W、SW、S、SE,其中
0 代表 0°~45°,1 代表 45°~90°,2 代表-90°~-45°,3 代表-45°~0°。像素点 P 的 梯度方向为 theta,则像素点 P1 和 P2 的梯度线性插值为:
o \mathrm{o} o 代表 O ∘ ∼ 4 5 ∘ , 1 \mathrm{O}^{\circ} \sim 45^{\circ}, 1 O∘∼45∘,1 代表 4 5 ∘ ∼ 9 0 ∘ , 2 45^{\circ} \sim 90^{\circ}, 2 45∘∼90∘,2 代表 − 9 0 ∘ ∼ − 4 5 ∘ , 3 -90^{\circ} \sim-45^{\circ}, 3 −90∘∼−45∘,3 代表 − 4 5 ∘ ∼ 0 ∘ -45^{\circ} \sim 0^{\circ} −45∘∼0∘ 。像素点 P \mathrm{P} P 的 梯度方向为 theta, 则像素点 P1 和 P 2 \mathrm{P} 2 P2 的梯度线性揷值为:
tan ( θ ) = G y / G x G p 1 = ( 1 − tan ( θ ) ) × E + tan ( θ ) × N E G p 2 = ( 1 − tan ( θ ) ) × W + tan ( θ ) × S W \begin{aligned} & \tan (\theta)=G_y / G_x \\ & G_{p 1}=(1-\tan (\theta)) \times E+\tan (\theta) \times N E \\ & G_{p 2}=(1-\tan (\theta)) \times W+\tan (\theta) \times S W \end{aligned} tan(θ)=Gy/GxGp1=(1−tan(θ))×E+tan(θ)×NEGp2=(1−tan(θ))×W+tan(θ)×SW
因此非极大值抑制的伪代码描写如下:if $G_p \geq G_{p 1}$ and $G_p \geq G_{p 2}$ $G_p$ may be an edge else $G_p$ should be sup pressed备注: 如何标志方向并不重要, 重要的是梯度方向的计算要和梯度算子的选取保持一致。
-
双阈值检测
在施加非极大值抑制之后,剩余的像素可以更准确地表示图像中的实际边缘。然而,仍 然存在由于噪声和颜色变化引起的一些边缘像素。为了解决这些杂散响应,必须用弱梯度值 过滤边缘像素,并保留具有高梯度值的边缘像素,可以通过选择高低阈值来实现。如果边缘 像素的梯度值高于高阈值,则将其标记为强边缘像素;如果边缘像素的梯度值小于高阈值并 且大于低阈值,则将其标记为弱边缘像素;如果边缘像素的梯度值小于低阈值,则会被抑制。 阈值的选择取决于给定输入图像的内容。
双阈值检测的伪代码描写如下:
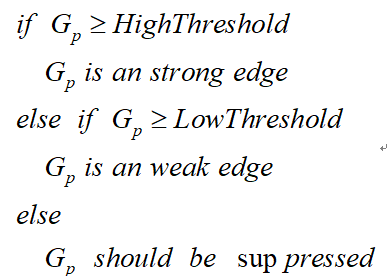
6**.** 通过抑制孤立的弱边缘完成边缘检测
被划分为强边缘的像素点已经被确定为边缘,因为它们是从图像中的真实 边缘中提取出来的。然而,对于弱边缘像素,将会有一些争论,因为这些像素可以从真实边 缘提取也可以是因噪声或颜色变化引起的。为了获得准确的结果,应该抑制由后者引起的弱 边缘。通常,由真实边缘引起的弱边缘像素将连接到强边缘像素,而噪声响应未连接。为了 跟踪边缘连接,通过查看弱边缘像素及其 8 个邻域像素,只要其中一个为强边缘像素,则该 弱边缘点就可以保留为真实的边缘。
抑制孤立边缘点的伪代码描述如下:

- 二值化图像输出结果
将结果二值化输出,即将图像上的像素点的灰度值设置为 0 或 255,也就是将整个图像 呈现出明显的黑白效果的过程。
4.4 Canny算子优缺点
- Canny 算子在二维空间的检测效果、定位性能及抗噪性能方面都更要优于LOG 算 子。
- Canny 算子的不足之处是对于无噪声的图像会使图像边缘变模糊。
- 为使检测效果更好,我们在运用该算子时一般选取稍大的滤波尺度,但是这样做易使图像的某些边缘细节特征丢失掉。
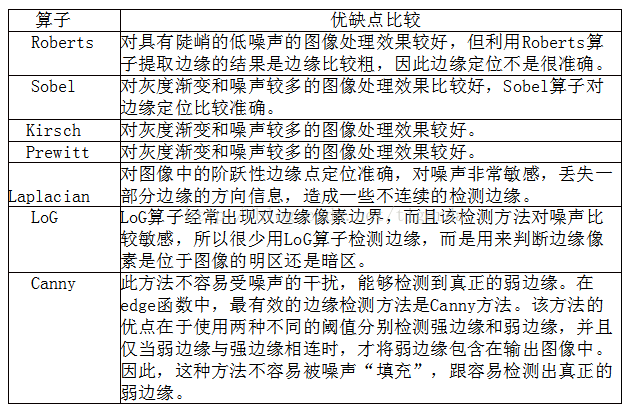
5.各边缘检测算子对比
第四章 SUSAN 边缘及角点检测方法
1 SUSAN 检测方法概述
SUSAN 检测方法是一种基于窗口模板的检测方法,主要是通过在图像每个像素点位置 处建立一个窗口,这个窗口是圆形的,这里为了得到各方向同性的响应,窗口内可以是常数 权值或高斯权值,一般情况下,窗口半径为 3.4 个像素(即窗口内总有 37 个像素)。 这样的窗口模板被放置在每个像素的位置,确定点之间强度相似程度可以由下面的图来描述,这里的 x 轴是指像素点之间强度差别,y 轴指的相似程度,为 1 就指完全相似。
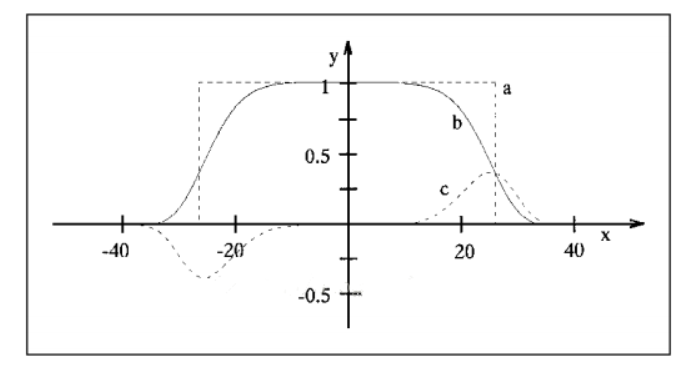
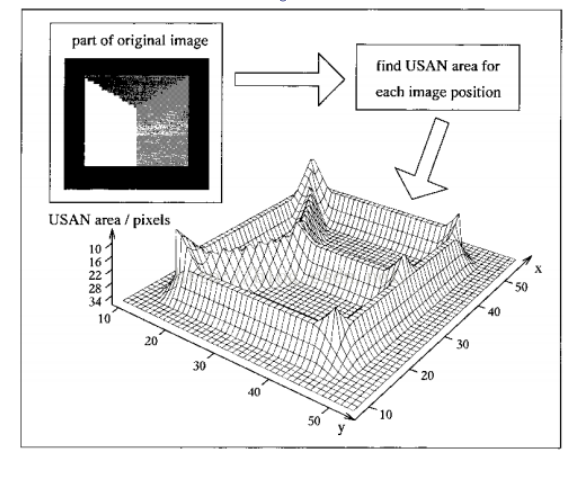
考虑为了运算简单,一般情况下使用 a 线(上图),最后统计所以同中心点相似的点数 (即相似程度为 1 的点)相似点所在区域被称为 USAN(Univalue Segment Assimilating Nucleus),而特征边缘或角点就是在这个点数值局部最小地方。图中的分界点(区分是否 相似的像素差别)实际上反映了图像特征的最小对比程度,及被排除噪声的最大数目。
-
边缘及角点检测没有用到图像像素的梯度(导数),因为这个原因,所以即使在噪声存在情况下,也能有好的表现。因为只要噪声足够的少,没有包含到所有相似像素的点, 那么噪声就可以被排除。在计算时,单个值的集合统一消除了噪声的影响, 对于噪声具有较好的鲁棒性。
-
通过比较像素点邻域同其中心相似程度,所以也具有了光强变化不变性(因 为像素点差别不会变化),及旋转不变性(旋转不会改变局部像素间的相似程度),及一定程 度的尺度不变性(角点的角度在尺度放大并不会变化,这里的一定程度是指在尺度放大时, 局部的曲度会慢慢平滑)。
-
使用的参数也非常的少,所以对于计算量及储存量 要求低。
-
主要是为针对于边缘检测和角点检测的,然后其对于噪声较高的鲁棒性,也会用于在噪声消除中,被用于去选择最佳局部平滑邻域(相似程度的点最多的地方)。本文重点描述 SUSAN 方法用于边缘检测和角点检测的思路,并简要介绍下 SUSAN方法是如何应用于噪声消除领域的。
2 SUSAN 边缘检测
SUSAN 边缘检测总共包括 5 个步骤:边缘响应的计算;边缘方向的计算;非极大值抑 制;子像素精度和检测位置。具体的检测过程如下。
1.边缘响应的计算
首先考虑到图像以每点像素为中心的圆形模板 (半径为 3.4 3.4 3.4 个像素, 模板内共有 37 个 像素), 对于其内的每个邻域点都作如下相似度衡量的计算 (标准是上图的 a \mathrm{a} a 线), 这里的 r \mathrm{r} r 是领域像素距离中心的长度, 而 ro 是中心位置, t \mathrm{t} t 指相似度分界值 (其决定了特征同背景的 最小区别程度, 及最大可被排除的噪声数)。
c ( r ⃗ , r 0 → ) = { 1 if ∣ I ( r ⃗ ) − I ( r ⃗ 0 ) ∣ ≤ t 0 if ∣ I ( r ⃗ ) − I ( r 0 → ) ∣ > t , c\left(\vec{r}, \overrightarrow{r_0}\right)= \begin{cases}1 & \text { if }\left|I(\vec{r})-I\left(\vec{r}_0\right)\right| \leq t \\ 0 & \text { if }\left|I(\vec{r})-I\left(\overrightarrow{r_0}\right)\right|>t,\end{cases} c(r,r0)={
10 if ∣I(r)−I(r0)∣≤t if
I(r)−I(r0)
>t,
当然我们也可以用平滑的线来从代替这种直接的分割方式 (如下图 b \mathrm{b} b 线), 这样可以获 得更稳定而敏感的结果, 虽然计算复杂但是可以通过查找表来获得较快的速度。公式如下:
c ( r ⃗ , r ⃗ 0 ) = e − ( I ( r ⃗ ) − I ( r 0 → ) I ) 6 . c\left(\vec{r}, \vec{r}_0\right)=e^{-\left(\frac{I(\vec{r})-I\left(\overrightarrow{r_0}\right)}{I}\right)^6} . c(r,r0)=e−(II(r)−I(r0))6.
并计算总共的相似程度:
n ( r ⃗ 0 ) = ∑ r ⃗ c ( r ⃗ , r 0 → ) n\left(\vec{r}_0\right)=\sum_{\vec{r}} c\left(\vec{r}, \overrightarrow{r_0}\right) n(r0)=r∑c(r,r0)
接下来, 将 n \mathrm{n} n 同一个固定的阈值 g \mathrm{g} g 比较 (一般设置为最大同中心相似点数 n m a x \mathrm{nmax} nmax 的 0.75 0.75 0.75 倍左右), 初始的边缘响应可以用下面等式计算:
R ( r ⃗ 0 ) = { g − n ( r ⃗ 0 ) if n ( r 0 → ) < g 0 otherwise R\left(\vec{r}_0\right)= \begin{cases}g-n\left(\vec{r}_0\right) & \text { if } n\left(\overrightarrow{r_0}\right)<g \\ 0 & \text { otherwise }\end{cases} R(r0)={
g−n(r0)0 if n(r0)<g otherwise
这里 g \mathrm{g} g 是为了排除噪声的影响, 而当 n \mathrm{n} n 小于这个阈值时, 才能被考虑其的边缘是否是边缘, n \mathrm{n} n 越小, 其边缘响应就越大。如果一个阶跃边缘被考虑, 如果这个点在边缘上, 那么 其 USAN 的值应当是小于或等于 0.5 0.5 0.5 倍的最大值, 而对于曲线边缘来说, 这个值应该会更 (因为曲度会更小, 所以在窗口内, 曲线内的区域会更小), 所以 g \mathrm{g} g 的加入不会影响原来 的边缘检测的结果的 (即所得的边缘响应 R R R 是不会为 0 的)。
2.边缘方向的计算
-
首先,非极大值抑制需要找到边缘方向(这个之后再解释)
-
确定子像素级精度也需要找到边缘方向(这个好理解)
-
一些应用可以会用到边 缘方向(也包括位置及长度),一个像素若其边缘长度不会 0,那么便有边缘方向,边缘一 般有两种情况:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kUBumiUc-1672324092174)(C:/Users/CWF/AppData/Roaming/Typora/typora-user-images/image-20221229210103725.png)]
一种是标准的边缘点(如同中的 a 和 b,其刚好位于边缘的一边或另一边),而 c 是另 一种情况,其刚好位于左右两边的过渡带间,而过渡带的强度恰好为左右像素强度的一半。 这里还引入了一个概念,USAN 的引力中心(USAN 区域即图像模板内的白色区域,就是同 中心相似的区域),其可以由下式计算:
r ⃗ ‾ ( r ⃗ 0 ) = ∑ r ⃗ r ⃗ c ( r ⃗ , r ⃗ 0 ) ∑ r ⃗ c ( r ⃗ , r ⃗ 0 ) \overline{\vec{r}}\left(\vec{r}_0\right)=\frac{\sum_{\vec{r}} \vec{r} c\left(\vec{r}, \vec{r}_0\right)}{\sum_{\vec{r}} c\left(\vec{r}, \vec{r}_0\right)} r(r0)=∑rc(r,r0)∑rrc(r,r0)
其中 a \mathrm{a} a 和 b \mathrm{b} b 情况可以被视一种像素间边缘, 引力中心同模板中心的向量恰好垂直于局 部边缘方向, 我们可以通过这种方式来找到其边缘方向。
而上图 c \mathrm{c} c 的情况就完全不一样了, 其引力中心同模板中心恰好在一点上 (这被视为一种 像素内边缘), 此时边缘的方向就要找到 USAN 区域内最长的对称轴方向, 这个可以通过如 下公式来获得:
( x − x 0 ) 2 ‾ ( r 0 → ) = ∑ r ⃗ ( x − x 0 ) 2 c ( r ⃗ , r 0 → ) ( y − y 0 ) 2 ‾ ( r 0 → ) = ∑ r ⃗ ( y − y 0 ) 2 c ( r ⃗ , r ⃗ 0 ) ( x − x 0 ) ( y − y 0 ) ‾ ( r 0 → ) = ∑ r ⃗ ( x − x 0 ) ( y − y 0 ) c ( r ⃗ , r 0 → ) \begin{gathered} \overline{\left(x-x_0\right)^2}\left(\overrightarrow{r_0}\right)=\sum_{\vec{r}}\left(x-x_0\right)^2 c\left(\vec{r}, \overrightarrow{r_0}\right) \\ \overline{\left(y-y_0\right)^2}\left(\overrightarrow{r_0}\right)=\sum_{\vec{r}}\left(y-y_0\right)^2 c\left(\vec{r}, \vec{r}_0\right) \\ \overline{\left(x-x_0\right)\left(y-y_0\right)}\left(\overrightarrow{r_0}\right)=\sum_{\vec{r}}\left(x-x_0\right)\left(y-y_0\right) c\left(\vec{r}, \overrightarrow{r_0}\right) \end{gathered} (x−x0)2(r0)=r∑(x−x0)2c(r,r0)(y−y0)2(r0)=r∑(y−y0)2c(r,r0)(x−x0)(y−y0)(r0)=r∑(x−x0)(y−y0)c(r,r0)
前两项的比值可以用于确定边缘的方向 (度数), 而后一项的符号用于确定一个倾斜边 缘其梯度的符号 (往那边倾斜)。
接下来的问题就是如何自动决定每点是属于以上哪种的边缘, 首先如果 USAN 区域 (像 素数) 比模板直径 (像素数) 要小, 那么这应该是像素内边缘 (如 c)。如果要大的话, 然后 又找到 USAN 的引力中心, 那么这应该是像素间边缘情况 (如 a \mathrm{a} a 和 b \mathrm{b} b )。如果引力中心同模 板中心的距离小于 1 个像素的话, 此时用于像素内边缘情况 (如 c) 来计算更为精确。
3.非极大值抑制
CANNY 算子中已有介绍,此处不再赘述。
4.子像素精度
对于每一个边缘点,首先找到边缘方向,然后在边缘垂直方向上减少边缘宽度,之后剩 下的边缘点做 3 点二次曲线拟合,而曲线的转折点(一般情况下同最初边缘点的距离应当少 于半个像素)被视为边缘的精确位置。
5.检测位置并不依赖于窗口大小
即窗口模板增大,不会改变检测的边缘的位置,即 SUSAN 具有尺度不变性,另外其对 于视点改变后的图像检测重复率也非常高,因为视点变化不会影响其角点是否存在。
3 SUSAN 角点检测
1.排除误检的角点
首先找到 USAN 的引力中心,然后计算引力中心同模板中心的距离,当 USAN 恰好能 指示一个正确角点时,其引力中心同模板中心将不会靠得太近,而如果是条细线的话,引力 中心同模板中心将会很近(如上图 a 和 b 所示)。另外的操作就是要加强 USAN 的邻近连续 性,在真实图像里,非常容易出现小的噪声点,而这些噪声点可能分布于 USAN 内。所以 对于模板内所有的像素,如果其是位于引力中心同模板中心所连的直线上,那么都应该视为USAN 的一部分。
2.非极大值抑制
SUSAN 角点检测方法同基于导数检测方法一个非常大的优势在于,其不会在靠近中心 相邻的区域不会与中心区域的角响应很难区分,所以局部的非极大值抑制中需要简单地选择 局部的最大值就可以了。
4 SUSAN 噪声滤波方法
SUSAN 噪声滤波方法主要是通过仅平滑那些同中心像素相似的区域(即 USAN),而由 此保留图像的结构信息。而 USAN 的平滑主要就是找到其中所以像素的平均值,而不会对 其相邻的不相关区域进行操作。
不过在区分相似度的公式上,却没有用到原来的公式,而是如下:
c ( r ⃗ , r ⃗ 0 ) = e − ( I ( r ⃗ ) − I ( r ⃗ 0 ) t ) 2 c\left(\vec{r}, \vec{r}_0\right)=e^{-\left(\frac{I(\vec{r})-I\left(\vec{r}_0\right)}{t}\right)^2} c(r,r0)=e−(tI(r)−I(r0))2
滤波器的最终公式为:
J ( x , y ) = ( ∑ i ≠ 0 , j ≠ 0 I ( x + i , y + j ) ∗ \begin{aligned} & J(x, y)=\left(\sum_{i \neq 0, j \neq 0} I(x+i, y+j) *\right. \\ & \end{aligned} J(x,y)=
i=0,j=0∑I(x+i,y+j)∗
第五章 *新兴的边缘检测算法
1 小波分析
1986 年,小波分析在 Y.Meyer , S.Mallat 与 I.Daubechies 等的研究工作基础上迅 速地发展起来,成为一门新兴的学科,并在信号处理中应用相当广泛。小波变换的理论基础 是傅里叶变换,它具有多尺度特征,如当尺度较大时,可以很好的滤除噪声,但不能很精确 的检测到边缘;当尺度较小时,能够检测到很好的边缘信息,但图像的去噪效果较差。因此 可以把用多种尺度来检测边缘而得到的结果相结合,充分利用各种尺度的优点,来得到更精 确的检测结果。
目前,有很多不同的小波边缘检测算法,主要差别在于采用的小波变换函数不同,常用 的小波函数包括: Morlet 小波、 Daubechies 小波、 Harr 小波、Mexican Hat 小波、 Hermite 小波、 Mallet 小波、基于高斯函数的小波及基于 B 样条的小波等。
2 模糊算法
在上世纪 80 年代中期, Pal 与 King 等人率先提出了一种模糊算法用来检测图像的 边缘,可以很好地把目标物体从背景中提取出来。基于模糊算法的图像边缘检测步骤如下: (1) 把隶属度函数 G 作用在图像上,得到的映像为“模糊的隶属度矩阵”; (2) 反复对隶属度矩阵实行非线性变换,从而使真实的边缘更加明显,而伪边缘变弱; (3) 计算隶属度矩阵的?? −1 ( 逆 ) 矩阵; (4)采用“ max ”和“ min ”算子提取边缘。该算法存在的缺点是计算复杂,且一部分低 灰度值的边缘信息有所损失。
3 人工神经网络
利用人工神经网络 [36-38] 来提取边缘在近年来已经发展为一个新的研究方向,其本 质是视边缘检测为模式识别问题,以利用它需要输入的知识少及适合并行实现等的优势。其 思想与传统方法存在很大的不同,是先把输入图像映射到某种神经元网络,再把原始边缘图 这样的先验知识输入进去,然后进行训练,一直到学习过程收敛或者用户满意方可停止。用 神经网络方法来构造函数模型主要是依据训练。在神经网络的各种模型中,前馈神经网络应 用最为广泛,而最常用来训练前馈网络的是BP算法。用BP网络检测边缘的算法存在一 些缺点,如较慢的收敛速度,较差的数值稳定性,难以调整参数,对于实际应用的需求很难 满足。目前,Hopfield 神经网络算法和模糊神经网络算法在很多方面都有所应用。
神经网 络具有下面 5 种特性:
(1) 自组织性;
(2) 自学习性;
(3) 联想存储功能;
(4) 告诉寻求优化解的能力;
(5) 自适应性等。
以上神经网络的特性决定了它用来检测图像边缘的可用性。
相关代码实
第六章 相关代码
1. 头文件imgFeat.h 实现
#include "imgFeat.h"
void feat::extBlobFeat(Mat& imgSrc, vector<SBlob>& blobs)
{
double dSigmaStart = 2;
double dSigmaEnd = 15;
double dSigmaStep = 1;
Mat image;
cvtColor(imgSrc, image, cv::COLOR_BGR2RGB);
image.convertTo(image, CV_64F);
vector<double> ivecSigmaArray;
double dInitSigma = dSigmaStart;
while (dInitSigma <= dSigmaEnd)
{
ivecSigmaArray.push_back(dInitSigma);
dInitSigma += dSigmaStep;
}
int iSigmaNb = ivecSigmaArray.size();
vector<Mat> matVecLOG;
for (size_t i = 0; i != iSigmaNb; i++)
{
double iSigma = ivecSigmaArray[i];
Size kSize(6 * iSigma + 1, 6 * iSigma + 1);
Mat HOGKernel = getHOGKernel(kSize, iSigma);
Mat imgLog;
filter2D(image, imgLog, -1, HOGKernel); // why imgLog must be an empty mat ?
imgLog = imgLog * iSigma *iSigma;
matVecLOG.push_back(imgLog);
}
vector<SBlob> allBlobs;
for (size_t k = 1; k != matVecLOG.size() - 1 ;k++)
{
Mat topLev = matVecLOG[k + 1];
Mat medLev = matVecLOG[k];
Mat botLev = matVecLOG[k - 1];
for (int i = 1; i < image.rows - 1; i++)
{
double* pTopLevPre = topLev.ptr<double>(i - 1);
double* pTopLevCur = topLev.ptr<double>(i);
double* pTopLevAft = topLev.ptr<double>(i + 1);
double* pMedLevPre = medLev.ptr<double>(i - 1);
double* pMedLevCur = medLev.ptr<double>(i);
double* pMedLevAft = medLev.ptr<double>(i + 1);
double* pBotLevPre = botLev.ptr<double>(i - 1);
double* pBotLevCur = botLev.ptr<double>(i);
double* pBotLevAft = botLev.ptr<double>(i + 1);
for (int j = 1; j < image.cols - 1; j++)
{
if ((pMedLevCur[j] >= pMedLevCur[j + 1] && pMedLevCur[j] >= pMedLevCur[j -1] &&
pMedLevCur[j] >= pMedLevPre[j + 1] && pMedLevCur[j] >= pMedLevPre[j -1] && pMedLevCur[j] >= pMedLevPre[j] &&
pMedLevCur[j] >= pMedLevAft[j + 1] && pMedLevCur[j] >= pMedLevAft[j -1] && pMedLevCur[j] >= pMedLevAft[j] &&
pMedLevCur[j] >= pTopLevPre[j + 1] && pMedLevCur[j] >= pTopLevPre[j -1] && pMedLevCur[j] >= pTopLevPre[j] &&
pMedLevCur[j] >= pTopLevCur[j + 1] && pMedLevCur[j] >= pTopLevCur[j -1] && pMedLevCur[j] >= pTopLevCur[j] &&
pMedLevCur[j] >= pTopLevAft[j + 1] && pMedLevCur[j] >= pTopLevAft[j -1] && pMedLevCur[j] >= pTopLevAft[j] &&
pMedLevCur[j] >= pBotLevPre[j + 1] && pMedLevCur[j] >= pBotLevPre[j -1] && pMedLevCur[j] >= pBotLevPre[j] &&
pMedLevCur[j] >= pBotLevCur[j + 1] && pMedLevCur[j] >= pBotLevCur[j -1] && pMedLevCur[j] >= pBotLevCur[j] &&
pMedLevCur[j] >= pBotLevAft[j + 1] && pMedLevCur[j] >= pBotLevAft[j -1] && pMedLevCur[j] >= pBotLevAft[j] ) ||
(pMedLevCur[j] < pMedLevCur[j + 1] && pMedLevCur[j] < pMedLevCur[j -1] &&
pMedLevCur[j] < pMedLevPre[j + 1] && pMedLevCur[j] < pMedLevPre[j -1] && pMedLevCur[j] < pMedLevPre[j] &&
pMedLevCur[j] < pMedLevAft[j + 1] && pMedLevCur[j] < pMedLevAft[j -1] && pMedLevCur[j] < pMedLevAft[j] &&
pMedLevCur[j] < pTopLevPre[j + 1] && pMedLevCur[j] < pTopLevPre[j -1] && pMedLevCur[j] < pTopLevPre[j] &&
pMedLevCur[j] < pTopLevCur[j + 1] && pMedLevCur[j] < pTopLevCur[j -1] && pMedLevCur[j] < pTopLevCur[j] &&
pMedLevCur[j] < pTopLevAft[j + 1] && pMedLevCur[j] < pTopLevAft[j -1] && pMedLevCur[j] < pTopLevAft[j] &&
pMedLevCur[j] < pBotLevPre[j + 1] && pMedLevCur[j] < pBotLevPre[j -1] && pMedLevCur[j] < pBotLevPre[j] &&
pMedLevCur[j] < pBotLevCur[j + 1] && pMedLevCur[j] < pBotLevCur[j -1] && pMedLevCur[j] < pBotLevCur[j] &&
pMedLevCur[j] < pBotLevAft[j + 1] && pMedLevCur[j] < pBotLevAft[j -1] && pMedLevCur[j] < pBotLevAft[j] ))
{
SBlob blob;
blob.position = Point(j, i);
blob.sigma = ivecSigmaArray[k];
blob.value = pMedLevCur[j];
allBlobs.push_back(blob);
}
}
}
}
vector<bool> delFlags(allBlobs.size(), true);
for (size_t i = 0; i != allBlobs.size(); i++)
{
if (delFlags[i] == false)
{
continue;
}
for (size_t j = i; j != allBlobs.size(); j++)
{
if (delFlags[j] == false)
{
continue;
}
double distCent = sqrt((allBlobs[i].position.x - allBlobs[j].position.x) * (allBlobs[i].position.x - allBlobs[j].position.x) +
(allBlobs[i].position.y - allBlobs[j].position.y) * (allBlobs[i].position.y - allBlobs[j].position.y));
if ((allBlobs[i].sigma + allBlobs[j].sigma) / distCent > 2)
{
if (allBlobs[i].value >= allBlobs[j].value)
{
delFlags[j] = false;
delFlags[i] = true;
}
else
{
delFlags[i] = false;
delFlags[j] = true;
}
}
}
}
for (size_t i = 0; i != allBlobs.size(); i++)
{
if (delFlags[i])
{
blobs.push_back(allBlobs[i]);
}
}
sort(blobs.begin(), blobs.end(), compareBlob);
}
Mat feat::getHOGKernel(Size& ksize, double sigma)
{
Mat kernel(ksize, CV_64F);
Point centPoint = Point((ksize.width -1)/2, ((ksize.height -1)/2));
// first calculate Gaussian
for (int i=0; i < kernel.rows; i++)
{
double* pData = kernel.ptr<double>(i);
for (int j = 0; j < kernel.cols; j++)
{
double param = -((i - centPoint.y) * (i - centPoint.y) + (j - centPoint.x) * (j - centPoint.x)) / (2*sigma*sigma);
pData[j] = exp(param);
}
}
double maxValue;
minMaxLoc(kernel, NULL, &maxValue);
for (int i=0; i < kernel.rows; i++)
{
double* pData = kernel.ptr<double>(i);
for (int j = 0; j < kernel.cols; j++)
{
if (pData[j] < EPS* maxValue)
{
pData[j] = 0;
}
}
}
double sumKernel = sum(kernel)[0];
if (sumKernel != 0)
{
kernel = kernel / sumKernel;
}
// now calculate Laplacian
for (int i=0; i < kernel.rows; i++)
{
double* pData = kernel.ptr<double>(i);
for (int j = 0; j < kernel.cols; j++)
{
double addition = ((i - centPoint.y) * (i - centPoint.y) + (j - centPoint.x) * (j - centPoint.x) - 2*sigma*sigma)/(sigma*sigma*sigma*sigma);
pData[j] *= addition;
}
}
// make the filter sum to zero
sumKernel = sum(kernel)[0];
kernel -= (sumKernel/(ksize.width * ksize.height));
return kernel;
}
bool feat::compareBlob(const SBlob& lhs, const SBlob& rhs)
{
return lhs.value > rhs.value;
}
2.sobel 算法实现
#include "imgFeat.h"
void feat::extBlobFeat(Mat& imgSrc, vector<SBlob>& blobs)
{
double dSigmaStart = 2;
double dSigmaEnd = 15;
double dSigmaStep = 1;
Mat image;
cvtColor(imgSrc, image, cv::COLOR_BGR2RGB);
image.convertTo(image, CV_64F);
vector<double> ivecSigmaArray;
double dInitSigma = dSigmaStart;
while (dInitSigma <= dSigmaEnd)
{
ivecSigmaArray.push_back(dInitSigma);
dInitSigma += dSigmaStep;
}
int iSigmaNb = ivecSigmaArray.size();
vector<Mat> matVecLOG;
for (size_t i = 0; i != iSigmaNb; i++)
{
double iSigma = ivecSigmaArray[i];
Size kSize(6 * iSigma + 1, 6 * iSigma + 1);
Mat HOGKernel = getHOGKernel(kSize, iSigma);
Mat imgLog;
filter2D(image, imgLog, -1, HOGKernel); // why imgLog must be an empty mat ?
imgLog = imgLog * iSigma *iSigma;
matVecLOG.push_back(imgLog);
}
vector<SBlob> allBlobs;
for (size_t k = 1; k != matVecLOG.size() - 1 ;k++)
{
Mat topLev = matVecLOG[k + 1];
Mat medLev = matVecLOG[k];
Mat botLev = matVecLOG[k - 1];
for (int i = 1; i < image.rows - 1; i++)
{
double* pTopLevPre = topLev.ptr<double>(i - 1);
double* pTopLevCur = topLev.ptr<double>(i);
double* pTopLevAft = topLev.ptr<double>(i + 1);
double* pMedLevPre = medLev.ptr<double>(i - 1);
double* pMedLevCur = medLev.ptr<double>(i);
double* pMedLevAft = medLev.ptr<double>(i + 1);
double* pBotLevPre = botLev.ptr<double>(i - 1);
double* pBotLevCur = botLev.ptr<double>(i);
double* pBotLevAft = botLev.ptr<double>(i + 1);
for (int j = 1; j < image.cols - 1; j++)
{
if ((pMedLevCur[j] >= pMedLevCur[j + 1] && pMedLevCur[j] >= pMedLevCur[j -1] &&
pMedLevCur[j] >= pMedLevPre[j + 1] && pMedLevCur[j] >= pMedLevPre[j -1] && pMedLevCur[j] >= pMedLevPre[j] &&
pMedLevCur[j] >= pMedLevAft[j + 1] && pMedLevCur[j] >= pMedLevAft[j -1] && pMedLevCur[j] >= pMedLevAft[j] &&
pMedLevCur[j] >= pTopLevPre[j + 1] && pMedLevCur[j] >= pTopLevPre[j -1] && pMedLevCur[j] >= pTopLevPre[j] &&
pMedLevCur[j] >= pTopLevCur[j + 1] && pMedLevCur[j] >= pTopLevCur[j -1] && pMedLevCur[j] >= pTopLevCur[j] &&
pMedLevCur[j] >= pTopLevAft[j + 1] && pMedLevCur[j] >= pTopLevAft[j -1] && pMedLevCur[j] >= pTopLevAft[j] &&
pMedLevCur[j] >= pBotLevPre[j + 1] && pMedLevCur[j] >= pBotLevPre[j -1] && pMedLevCur[j] >= pBotLevPre[j] &&
pMedLevCur[j] >= pBotLevCur[j + 1] && pMedLevCur[j] >= pBotLevCur[j -1] && pMedLevCur[j] >= pBotLevCur[j] &&
pMedLevCur[j] >= pBotLevAft[j + 1] && pMedLevCur[j] >= pBotLevAft[j -1] && pMedLevCur[j] >= pBotLevAft[j] ) ||
(pMedLevCur[j] < pMedLevCur[j + 1] && pMedLevCur[j] < pMedLevCur[j -1] &&
pMedLevCur[j] < pMedLevPre[j + 1] && pMedLevCur[j] < pMedLevPre[j -1] && pMedLevCur[j] < pMedLevPre[j] &&
pMedLevCur[j] < pMedLevAft[j + 1] && pMedLevCur[j] < pMedLevAft[j -1] && pMedLevCur[j] < pMedLevAft[j] &&
pMedLevCur[j] < pTopLevPre[j + 1] && pMedLevCur[j] < pTopLevPre[j -1] && pMedLevCur[j] < pTopLevPre[j] &&
pMedLevCur[j] < pTopLevCur[j + 1] && pMedLevCur[j] < pTopLevCur[j -1] && pMedLevCur[j] < pTopLevCur[j] &&
pMedLevCur[j] < pTopLevAft[j + 1] && pMedLevCur[j] < pTopLevAft[j -1] && pMedLevCur[j] < pTopLevAft[j] &&
pMedLevCur[j] < pBotLevPre[j + 1] && pMedLevCur[j] < pBotLevPre[j -1] && pMedLevCur[j] < pBotLevPre[j] &&
pMedLevCur[j] < pBotLevCur[j + 1] && pMedLevCur[j] < pBotLevCur[j -1] && pMedLevCur[j] < pBotLevCur[j] &&
pMedLevCur[j] < pBotLevAft[j + 1] && pMedLevCur[j] < pBotLevAft[j -1] && pMedLevCur[j] < pBotLevAft[j] ))
{
SBlob blob;
blob.position = Point(j, i);
blob.sigma = ivecSigmaArray[k];
blob.value = pMedLevCur[j];
allBlobs.push_back(blob);
}
}
}
}
vector<bool> delFlags(allBlobs.size(), true);
for (size_t i = 0; i != allBlobs.size(); i++)
{
if (delFlags[i] == false)
{
continue;
}
for (size_t j = i; j != allBlobs.size(); j++)
{
if (delFlags[j] == false)
{
continue;
}
double distCent = sqrt((allBlobs[i].position.x - allBlobs[j].position.x) * (allBlobs[i].position.x - allBlobs[j].position.x) +
(allBlobs[i].position.y - allBlobs[j].position.y) * (allBlobs[i].position.y - allBlobs[j].position.y));
if ((allBlobs[i].sigma + allBlobs[j].sigma) / distCent > 2)
{
if (allBlobs[i].value >= allBlobs[j].value)
{
delFlags[j] = false;
delFlags[i] = true;
}
else
{
delFlags[i] = false;
delFlags[j] = true;
}
}
}
}
for (size_t i = 0; i != allBlobs.size(); i++)
{
if (delFlags[i])
{
blobs.push_back(allBlobs[i]);
}
}
sort(blobs.begin(), blobs.end(), compareBlob);
}
Mat feat::getHOGKernel(Size& ksize, double sigma)
{
Mat kernel(ksize, CV_64F);
Point centPoint = Point((ksize.width -1)/2, ((ksize.height -1)/2));
// first calculate Gaussian
for (int i=0; i < kernel.rows; i++)
{
double* pData = kernel.ptr<double>(i);
for (int j = 0; j < kernel.cols; j++)
{
double param = -((i - centPoint.y) * (i - centPoint.y) + (j - centPoint.x) * (j - centPoint.x)) / (2*sigma*sigma);
pData[j] = exp(param);
}
}
double maxValue;
minMaxLoc(kernel, NULL, &maxValue);
for (int i=0; i < kernel.rows; i++)
{
double* pData = kernel.ptr<double>(i);
for (int j = 0; j < kernel.cols; j++)
{
if (pData[j] < EPS* maxValue)
{
pData[j] = 0;
}
}
}
double sumKernel = sum(kernel)[0];
if (sumKernel != 0)
{
kernel = kernel / sumKernel;
}
// now calculate Laplacian
for (int i=0; i < kernel.rows; i++)
{
double* pData = kernel.ptr<double>(i);
for (int j = 0; j < kernel.cols; j++)
{
double addition = ((i - centPoint.y) * (i - centPoint.y) + (j - centPoint.x) * (j - centPoint.x) - 2*sigma*sigma)/(sigma*sigma*sigma*sigma);
pData[j] *= addition;
}
}
// make the filter sum to zero
sumKernel = sum(kernel)[0];
kernel -= (sumKernel/(ksize.width * ksize.height));
return kernel;
}
bool feat::compareBlob(const SBlob& lhs, const SBlob& rhs)
{
return lhs.value > rhs.value;
}
3. Hog实现
#include "imgFeat.h"
void feat::extBlobFeat(Mat& imgSrc, vector<SBlob>& blobs)
{
double dSigmaStart = 2;
double dSigmaEnd = 15;
double dSigmaStep = 1;
Mat image;
cvtColor(imgSrc, image, cv::COLOR_BGR2RGB);
image.convertTo(image, CV_64F);
vector<double> ivecSigmaArray;
double dInitSigma = dSigmaStart;
while (dInitSigma <= dSigmaEnd)
{
ivecSigmaArray.push_back(dInitSigma);
dInitSigma += dSigmaStep;
}
int iSigmaNb = ivecSigmaArray.size();
vector<Mat> matVecLOG;
for (size_t i = 0; i != iSigmaNb; i++)
{
double iSigma = ivecSigmaArray[i];
Size kSize(6 * iSigma + 1, 6 * iSigma + 1);
Mat HOGKernel = getHOGKernel(kSize, iSigma);
Mat imgLog;
filter2D(image, imgLog, -1, HOGKernel); // why imgLog must be an empty mat ?
imgLog = imgLog * iSigma *iSigma;
matVecLOG.push_back(imgLog);
}
vector<SBlob> allBlobs;
for (size_t k = 1; k != matVecLOG.size() - 1 ;k++)
{
Mat topLev = matVecLOG[k + 1];
Mat medLev = matVecLOG[k];
Mat botLev = matVecLOG[k - 1];
for (int i = 1; i < image.rows - 1; i++)
{
double* pTopLevPre = topLev.ptr<double>(i - 1);
double* pTopLevCur = topLev.ptr<double>(i);
double* pTopLevAft = topLev.ptr<double>(i + 1);
double* pMedLevPre = medLev.ptr<double>(i - 1);
double* pMedLevCur = medLev.ptr<double>(i);
double* pMedLevAft = medLev.ptr<double>(i + 1);
double* pBotLevPre = botLev.ptr<double>(i - 1);
double* pBotLevCur = botLev.ptr<double>(i);
double* pBotLevAft = botLev.ptr<double>(i + 1);
for (int j = 1; j < image.cols - 1; j++)
{
if ((pMedLevCur[j] >= pMedLevCur[j + 1] && pMedLevCur[j] >= pMedLevCur[j -1] &&
pMedLevCur[j] >= pMedLevPre[j + 1] && pMedLevCur[j] >= pMedLevPre[j -1] && pMedLevCur[j] >= pMedLevPre[j] &&
pMedLevCur[j] >= pMedLevAft[j + 1] && pMedLevCur[j] >= pMedLevAft[j -1] && pMedLevCur[j] >= pMedLevAft[j] &&
pMedLevCur[j] >= pTopLevPre[j + 1] && pMedLevCur[j] >= pTopLevPre[j -1] && pMedLevCur[j] >= pTopLevPre[j] &&
pMedLevCur[j] >= pTopLevCur[j + 1] && pMedLevCur[j] >= pTopLevCur[j -1] && pMedLevCur[j] >= pTopLevCur[j] &&
pMedLevCur[j] >= pTopLevAft[j + 1] && pMedLevCur[j] >= pTopLevAft[j -1] && pMedLevCur[j] >= pTopLevAft[j] &&
pMedLevCur[j] >= pBotLevPre[j + 1] && pMedLevCur[j] >= pBotLevPre[j -1] && pMedLevCur[j] >= pBotLevPre[j] &&
pMedLevCur[j] >= pBotLevCur[j + 1] && pMedLevCur[j] >= pBotLevCur[j -1] && pMedLevCur[j] >= pBotLevCur[j] &&
pMedLevCur[j] >= pBotLevAft[j + 1] && pMedLevCur[j] >= pBotLevAft[j -1] && pMedLevCur[j] >= pBotLevAft[j] ) ||
(pMedLevCur[j] < pMedLevCur[j + 1] && pMedLevCur[j] < pMedLevCur[j -1] &&
pMedLevCur[j] < pMedLevPre[j + 1] && pMedLevCur[j] < pMedLevPre[j -1] && pMedLevCur[j] < pMedLevPre[j] &&
pMedLevCur[j] < pMedLevAft[j + 1] && pMedLevCur[j] < pMedLevAft[j -1] && pMedLevCur[j] < pMedLevAft[j] &&
pMedLevCur[j] < pTopLevPre[j + 1] && pMedLevCur[j] < pTopLevPre[j -1] && pMedLevCur[j] < pTopLevPre[j] &&
pMedLevCur[j] < pTopLevCur[j + 1] && pMedLevCur[j] < pTopLevCur[j -1] && pMedLevCur[j] < pTopLevCur[j] &&
pMedLevCur[j] < pTopLevAft[j + 1] && pMedLevCur[j] < pTopLevAft[j -1] && pMedLevCur[j] < pTopLevAft[j] &&
pMedLevCur[j] < pBotLevPre[j + 1] && pMedLevCur[j] < pBotLevPre[j -1] && pMedLevCur[j] < pBotLevPre[j] &&
pMedLevCur[j] < pBotLevCur[j + 1] && pMedLevCur[j] < pBotLevCur[j -1] && pMedLevCur[j] < pBotLevCur[j] &&
pMedLevCur[j] < pBotLevAft[j + 1] && pMedLevCur[j] < pBotLevAft[j -1] && pMedLevCur[j] < pBotLevAft[j] ))
{
SBlob blob;
blob.position = Point(j, i);
blob.sigma = ivecSigmaArray[k];
blob.value = pMedLevCur[j];
allBlobs.push_back(blob);
}
}
}
}
vector<bool> delFlags(allBlobs.size(), true);
for (size_t i = 0; i != allBlobs.size(); i++)
{
if (delFlags[i] == false)
{
continue;
}
for (size_t j = i; j != allBlobs.size(); j++)
{
if (delFlags[j] == false)
{
continue;
}
double distCent = sqrt((allBlobs[i].position.x - allBlobs[j].position.x) * (allBlobs[i].position.x - allBlobs[j].position.x) +
(allBlobs[i].position.y - allBlobs[j].position.y) * (allBlobs[i].position.y - allBlobs[j].position.y));
if ((allBlobs[i].sigma + allBlobs[j].sigma) / distCent > 2)
{
if (allBlobs[i].value >= allBlobs[j].value)
{
delFlags[j] = false;
delFlags[i] = true;
}
else
{
delFlags[i] = false;
delFlags[j] = true;
}
}
}
}
for (size_t i = 0; i != allBlobs.size(); i++)
{
if (delFlags[i])
{
blobs.push_back(allBlobs[i]);
}
}
sort(blobs.begin(), blobs.end(), compareBlob);
}
Mat feat::getHOGKernel(Size& ksize, double sigma)
{
Mat kernel(ksize, CV_64F);
Point centPoint = Point((ksize.width -1)/2, ((ksize.height -1)/2));
// first calculate Gaussian
for (int i=0; i < kernel.rows; i++)
{
double* pData = kernel.ptr<double>(i);
for (int j = 0; j < kernel.cols; j++)
{
double param = -((i - centPoint.y) * (i - centPoint.y) + (j - centPoint.x) * (j - centPoint.x)) / (2*sigma*sigma);
pData[j] = exp(param);
}
}
double maxValue;
minMaxLoc(kernel, NULL, &maxValue);
for (int i=0; i < kernel.rows; i++)
{
double* pData = kernel.ptr<double>(i);
for (int j = 0; j < kernel.cols; j++)
{
if (pData[j] < EPS* maxValue)
{
pData[j] = 0;
}
}
}
double sumKernel = sum(kernel)[0];
if (sumKernel != 0)
{
kernel = kernel / sumKernel;
}
// now calculate Laplacian
for (int i=0; i < kernel.rows; i++)
{
double* pData = kernel.ptr<double>(i);
for (int j = 0; j < kernel.cols; j++)
{
double addition = ((i - centPoint.y) * (i - centPoint.y) + (j - centPoint.x) * (j - centPoint.x) - 2*sigma*sigma)/(sigma*sigma*sigma*sigma);
pData[j] *= addition;
}
}
// make the filter sum to zero
sumKernel = sum(kernel)[0];
kernel -= (sumKernel/(ksize.width * ksize.height));
return kernel;
}
bool feat::compareBlob(const SBlob& lhs, const SBlob& rhs)
{
return lhs.value > rhs.value;
}
4. canny实现
#include "imgFeat.h"
void feat::getCannyEdge(const Mat& imgSrc, Mat& imgDst, double lowThresh, double highThresh, double sigma)
{
Mat gray;
if (imgSrc.channels() == 3)
{
cvtColor(imgSrc, gray, cv::COLOR_BGR2GRAY);
}
else
{
gray = imgSrc.clone();
}
gray.convertTo(gray, CV_64F);
gray = gray / 255;
double gaussianDieOff = .0001;
double percentOfPixelsNotEdges = .7; // Used for selecting thresholds
double thresholdRatio = .4; // Low thresh is this fraction of the high
int possibleWidth = 30;
double ssq = sigma * sigma;
for (int i = 1; i <= possibleWidth; i++)
{
if (exp(-(i * i) / (2* ssq)) < gaussianDieOff)
{
possibleWidth = i - 1;
break;
}
}
if (possibleWidth == 30)
{
possibleWidth = 1; // the user entered a reallly small sigma
}
// get the 1D gaussian filter
int winSz = 2 * possibleWidth + 1;
Mat gaussKernel1D(1, winSz, CV_64F);
double* kernelPtr = gaussKernel1D.ptr<double>(0);
for (int i = 0; i < gaussKernel1D.cols; i++)
{
kernelPtr[i] = exp(-(i - possibleWidth) * (i - possibleWidth) / (2 * ssq)) / (2 * CV_PI * ssq);
}
// get the derectional derivatives of gaussian kernel
Mat dGaussKernel(winSz, winSz, CV_64F);
for (int i = 0; i < dGaussKernel.rows; i++)
{
double* linePtr = dGaussKernel.ptr<double>(i);
for (int j = 0; j< dGaussKernel.cols; j++)
{
linePtr[j] = - (j - possibleWidth) * exp(-((i - possibleWidth) * (i - possibleWidth) + (j - possibleWidth) * (j - possibleWidth)) / (2 * ssq)) / (CV_PI * ssq);
}
}
/* smooth the image out*/
Mat imgSmooth;
filter2D(gray, imgSmooth, -1, gaussKernel1D);
filter2D(imgSmooth, imgSmooth, -1, gaussKernel1D.t());
/*apply directional derivatives*/
Mat imgX, imgY;
filter2D(imgSmooth, imgX, -1, dGaussKernel);
filter2D(imgSmooth, imgY, -1, dGaussKernel.t());
Mat imgMag;
sqrt(imgX.mul(imgX) + imgY.mul(imgY), imgMag);
double magMax;
minMaxLoc(imgMag, NULL, &magMax, NULL, NULL);
if (magMax > 0 )
{
imgMag = imgMag / magMax;
}
if (lowThresh == -1 || highThresh == -1)
{
highThresh = getCannyThresh(imgMag, percentOfPixelsNotEdges);
lowThresh = thresholdRatio * highThresh;
}
Mat imgStrong = Mat::zeros(imgMag.size(), CV_8U);
Mat imgWeak = Mat::zeros(imgMag.size(), CV_8U);
for (int dir = 1; dir <= 4; dir++)
{
Mat gradMag1(imgMag.size(), imgMag.type());
Mat gradMag2(imgMag.size(), imgMag.type());
Mat idx = Mat::zeros(imgMag.size(), CV_8U);
if (dir == 1)
{
Mat dCof = abs(imgY / imgX);
idx = (imgY <= 0 & imgX > -imgY) | (imgY >= 0 & imgX < -imgY);
idx.row(0).setTo(Scalar(0));
idx.row(idx.rows - 1).setTo(Scalar(0));
idx.col(0).setTo(Scalar(0));
idx.col(idx.cols - 1).setTo(Scalar(0));
for (int i = 1; i < imgMag.rows - 1; i++)
{
for (int j = 1; j < imgMag.cols - 1; j++)
{
gradMag1.at<double>(i,j) = (1 - dCof.at<double>(i,j)) * imgMag.at<double>(i,j + 1) + dCof.at<double>(i,j) * imgMag.at<double>(i - 1,j + 1);
gradMag2.at<double>(i,j) = (1 - dCof.at<double>(i,j)) * imgMag.at<double>(i,j - 1) + dCof.at<double>(i,j) * imgMag.at<double>(i + 1,j - 1);
}
}
}
else if(dir == 2)
{
Mat dCof = abs(imgX / imgY);
idx = (imgX > 0 & -imgY >= imgX) | (imgX < 0 & -imgY <= imgX);
for (int i = 1; i < imgMag.rows - 1; i++)
{
for (int j = 1; j < imgMag.cols - 1; j++)
{
gradMag1.at<double>(i,j) = (1 - dCof.at<double>(i,j)) * imgMag.at<double>(i - 1,j) + dCof.at<double>(i,j) * imgMag.at<double>(i - 1,j + 1);
gradMag2.at<double>(i,j) = (1 - dCof.at<double>(i,j)) * imgMag.at<double>(i + 1,j) + dCof.at<double>(i,j) * imgMag.at<double>(i + 1,j - 1);
}
}
}
else if(dir == 3)
{
Mat dCof = abs(imgX / imgY);
idx = (imgX <= 0 & imgX > imgY) | (imgX >= 0 & imgX < imgY);
for (int i = 1; i < imgMag.rows - 1; i++)
{
for (int j = 1; j < imgMag.cols - 1; j++)
{
gradMag1.at<double>(i,j) = (1 - dCof.at<double>(i,j)) * imgMag.at<double>(i - 1,j) + dCof.at<double>(i,j) * imgMag.at<double>(i - 1,j - 1);
gradMag2.at<double>(i,j) = (1 - dCof.at<double>(i,j)) * imgMag.at<double>(i + 1,j) + dCof.at<double>(i,j) * imgMag.at<double>(i + 1,j + 1);
}
}
}
else
{
Mat dCof = abs(imgY / imgX);
idx = (imgY <0 & imgX <= imgY) | (imgY > 0 & imgX >= imgY);
for (int i = 1; i < imgMag.rows - 1; i++)
{
for (int j = 1; j < imgMag.cols - 1; j++)
{
gradMag1.at<double>(i,j) = (1 - dCof.at<double>(i,j)) * imgMag.at<double>(i,j - 1) + dCof.at<double>(i,j) * imgMag.at<double>(i - 1,j - 1);
gradMag2.at<double>(i,j) = (1 - dCof.at<double>(i,j)) * imgMag.at<double>(i,j + 1) + dCof.at<double>(i,j) * imgMag.at<double>(i + 1,j + 1);
}
}
}
Mat idxLocalMax = idx & ((imgMag >= gradMag1) & (imgMag >= gradMag2));
imgWeak = imgWeak | ((imgMag > lowThresh) & idxLocalMax);
imgStrong= imgStrong| ((imgMag > highThresh) & imgWeak);
}
imgDst = Mat::zeros(imgWeak.size(),imgWeak.type());
for (int i = 1; i < imgWeak.rows - 1; i++)
{
uchar* pWeak = imgWeak.ptr<uchar>(i);
uchar* pDst = imgDst.ptr<uchar>(i);
uchar* pStrPre = imgStrong.ptr<uchar>(i - 1);
uchar* pStrMid = imgStrong.ptr<uchar>(i);
uchar* pStrAft = imgStrong.ptr<uchar>(i + 1);
for (int j = 1; j < imgWeak.cols - 1; j++)
{
if (!pWeak[j])
{
continue;
}
if (pStrMid[j])
{
pDst[j] = 255;
}
if (pStrMid[j-1] || pStrMid[j+1] || pStrPre[j-1] || pStrPre[j] || pStrPre[j+1] || pStrAft[j-1] || pStrAft[j] ||pStrAft[j+1])
{
pDst[j] = 255;
}
}
}
}
double feat::getCannyThresh(const Mat& inputArray, double percentage)
{
double thresh = -1.0;
// compute the 64-hist of inputArray
int nBins = 64;
double minValue, maxValue;
minMaxLoc(inputArray, &minValue, &maxValue, NULL, NULL);
double step = (maxValue - minValue) / nBins;
vector<unsigned> histBin(nBins,0);
for (int i = 0; i < inputArray.rows; i++)
{
const double* pData = inputArray.ptr<double>(i);
for(int j = 0; j < inputArray.cols; j++)
{
int index = (pData[j] - minValue) / step;
histBin[index]++;
}
}
unsigned cumSum = 0;
for (int i = 0; i < nBins; i++)
{
cumSum += histBin[i];
if (cumSum > percentage * inputArray.rows * inputArray.cols)
{
thresh = (i + 1) / 64.0;
break;
}
}
return thresh;
}
main函数
#include "imgFeat.h"
int main(int argc, char** argv)
{
Mat image = imread("test.jpg");
Mat cornerMap;
feat::getSobelEdge(image ,cornerMap);
feat::drawCornerOnImage(image, cornerMap);
cv::namedWindow("corners");
cv::imshow("corners", image);
cv::waitKey();
return 0;
}