数据结构成神篇4：树（下）

Position Find( ElementType X, BinTree BST):从二叉搜索树BST中查找元素X，返回其所在结点的地址;
Position FindMin( BinTree BST ):从二叉搜索树BST中查找并返回最小元素所在结点的地址;
Position FindMax( BinTree BST):从二叉搜索树BST中查找并返回最大元素所在结点的地址。
P BinTree Insert( ElementType X, BinTree BST )
P BinTree Delete( ElementType X, BinTree BST )

1，Find（查找）

查找从根结点开始，如果树为空，返回NULL

若搜索树非空，则根结点关键字和X进行比较，并进行不同处理:
①若X小于根结点键值，只需在左子树中继续搜索;
②如果X大于根结点的键值，在右子树中进行继续搜索;
③若两者比较结果是相等，搜索完成，返回指向此结点的指针。.

代码实现：

尾递归：

Posi tion Find( ElementType X，BinTree BST )
{   
    if.(!BST)returnNULL;/*如果为空，返回NULL*/
    if.(X.>BST->Data)
        return FindT X, BST->Right ) ; /*在右子树中继续查找*,
    else if( X< BST->Data )
        return Find( x, BST->left ) ; /*在左子树中继续查找*/
    else     /* X == BST->Data */
        return BST; /*查找成功，返回结点的找到结点的地址*/
}

迭代函数：由于非递归函数的执行效率高，可将“尾递归” 函数改为迭代函数

Position IterFind( E1ementType X, BinTree BST )
{    
    while( BST ) {
        if( X > BST->Data )
            BST = BST->Right; /*向右子树中移动，继续查找*/
        else if( X < BST->Data )
            BST = BST->Ieft; /*向左子树中移动，继续查找*/
        else /* X == BST->Data */
            return BST; /*查找成功，返回结点的找到结点的地址*/
    }
    return NULL; /*查找失败*/
}

查找最大和最小元素
1）最大元素一定是在树的最右分枝的端结点上
2）最小元素一定是在树的最左分枝的端结点上

找最小元素：

Position FindMin( BinTree BST )
{
    if( !BST )     return NULL; /*空的二叉搜索树，返回NULL*/
    else if( !BST-> Left )
        return BST; / *找到最左叶结点并返回*/
    else
        return FindMin( BST->Left ) ; /*沿左分支继续查找*/
}

找最大元素：

Position FindMax( BinTree BST )
{
    if (BST )
        while ( BST-> >Right )
            BST = BST->Right ;
                /*沿右分支继续查找， 直到最右叶结点*/
    return BST ;
}

2，Insert（插入）

BinTree Insert( E1ementType X，BinTree BST )
{
    if( !BST ) {
        /*若原树为空， 生成并返回一个结点的二叉搜索树*/
        BST = malloc(sizeof (struct TreeNode) ) ;
        BST->Data = X;
        BST->Left = BST->Right = NULL;
    }else / *开始找要插入元素的位置*/
        if( X < BST->Data )
            BST->Left = Insert( X，BST-> Left) ;
                /*递归插入左子树*/
        else if( X > BST->Data )
            BST->Right = Insert( X, BST->Right) ;
                        /*递归插入右子树*/ .
        /* else x已经存在，什么都不做*/
    return BST ;
}

3，delete（删除）

1）删叶结点：

要删除的是叶结点:直接删除，并再修改其父结点指针--置为NULL

2）要删除的结点只有一个孩子结点:将其父结点的指针指向要删除结点的孩子结点

3）要删除的结点有左、右两棵子树:

用另一结点替代被删除结点:右子树的最小元素或者左子树的最大元素

代码实现：

BinTree Delete ( E1ementType X，BinTree BST )
{    
    Position Tmp;
    if( !BST ) printf ("要删除的元素未找到") ;
    else if ( X < BST->Data )
        BST->Left = Delete( x，BST->Ieft) ; /*左子树递归删除*/
    else if( X > BST->Data )
        BST->Right = Delete( X，BST->Right) ; /*右子树递归删除*/
    else / *找到要删除的结点*/
        if( BST->Left && BST->Right ) { /*被删除结点有左右两个子结点*/
            Tmp = FindMin( BST->Right ) ;
                /*在右子树中找最小的元素填充删除结点*/
            BST->Data = Tmp->Data;
            BST->Right = Delete( BST->Data， BST->Right) ;
                /*在删除结点的右子树中删除最小元素*/
        } else { /*被删除结点有一个或无子结点*/
            Tmp=BST;
            if( !BST->Ieft ) /* 有右孩子或无子结点*/
                BST = BST- >Right;
            else if( !BST->Right ) /*有左孩子或无子结点*/
                BST = BST->Left;
            free( Tmp ) ;
    return BST ;
}

平衡二叉树：

一，什么是平衡二叉树？

平衡因子( Balance Factor,简称BF) : BF(T)= hL-hR,其中hL和hR分别为T的左、右子树的高度。

平衡二叉树( Balanced Binary Tree) ( AVL树)
空树，或者
任一结点左、右子树高度差的绝对值不超过1，即|BF(T)|S 1

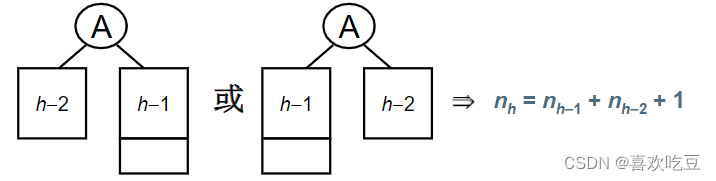
平衡二叉树的高度能达到log2n吗?
设nh高度为h的平衡二叉树的最少结点数。结点数最少时:

二，平衡二叉树的调整

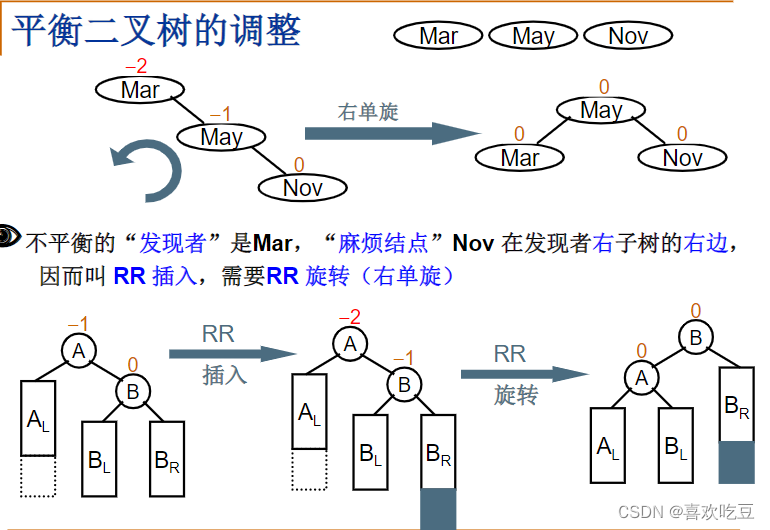
对二叉树的一些操作会导致其平衡失调，所以我们要对其做出调整。

1，右单旋

2，左单旋

3，左右单旋

4，右左单旋

堆（heap）：

优先队列(Priority Queue) :特殊的“队列”，取出元素的顺序是依照元素的优先权(关键字)大小，而不是元素进入队列的先后顺序。

1，问题:如何组织优先队列?

一般的数组、链表?
有序的数组或者链表?
二叉搜索树? AVL树?

2，是否可以采用二叉树存储结构?

二叉搜索树?
如果采用二叉树结构，应更关注插入还是删除?
➢树结点顺序怎么安排?
➢树结构怎样?

➢堆的两个特性
结构性:用数组表示的完全二叉树;
有序性:任一结点的关键字是其子树所有结点的最大值(或最小值)

最大堆(MaxHeap)”,也称“大顶堆”:最大值
最小堆(MinHeap)” ,也称“小顶堆”:最小值

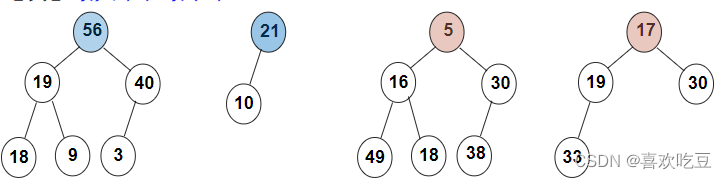
一，堆的抽象数据类型描述

类型名称:最大堆(MaxHeap)
数据对象集:完全二叉树，每个结点的元素值不小于其子结点的元素值
操作集:最大堆H∈MaxHeap,元素item∈ElementType,主要操作有:
●MaxHeap Create( int MaxSize ):创建一 - 个空的最大堆。
●Boolean IsFull( MaxHeap H):判断最大堆H是否已满。
●Insert( MaxHeap H, ElementType item):将元素item插入最大堆H。
●Boolean IsEmpty( MaxHeap H );判断最大堆H是否为空。
●ElementType DeleteMax( MaxHeap H):返回H中最大元素(高优先级)。

1，最大堆的创建：

typedef struct HeapStruct *MaxHeap;
struct HeapStruct {
    ElementType *Elements; /* 存储堆元素首地址*/
    int Size;/*堆的当前元素个数*/
    int Capacity;/*堆的最大容量/
};

MaxHeap Create ( int MaxSize )
{
    /*创建容量为MaxSize的空的最大堆*/
    MaxHeap H = malloc( sizeof( struct HeapStruct ) ) ;
    H->Elements = mal1oc( (MaxSize+1) * sizeof (ElementType) ) ;
    H->Size = 0 ;
    H- >Capacity = MaxSize;
    H->Elements[0] = MaxData ;
        /*定义“哨兵”为大于堆中所有可能元素的值，便于以后更快操作*/
    return H ;
}

2，最大堆的插入：

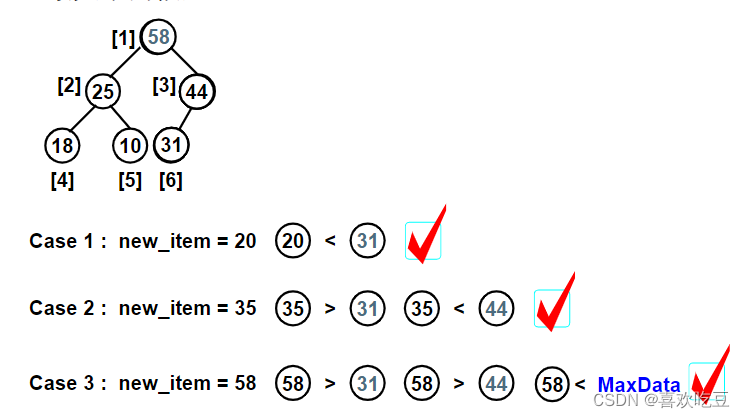
将新增结点插入到从其父结点到根结点的有序序列中

void Insert( MaxHeap H，ElementType item )
{ /*将元素item插入最大堆H，其中H->Elements[0]已经定义为哨兵*/
    int i;
    if ( IsFu11(H) ) {
        printf ("最大堆已满") ;
        return;
    }
    i = ++H->Size; /* i指向插入后堆中的最后一个元素的位置*/
    for ( ; H->E1ements[i/2] < item ; i/=2 )
        H->E1ements[i] = H->Elements[i/2]; /*向下过滤结点*/
        H->E1ements[i] = item; /*将item插入*/
}

哨兵的作用：i>1

T(N)=O(logN)

3，最大堆的删除：

取出根结点(最大值)元素，同时删除堆的一个结点。

ElementType DeleteMax( MaxHeap H )
{ /*从最大堆8中取出键值为最大的元素，并删除-一个结点*/
    int Parent， Child;
    E1ementType MaxItem，temp ;
    if ( IsEmpty (H) ) {
        printf ("最大堆已为空") ;
        return ;
    }
    MaxItem = H->E1ements[1]; /*取出根结点最大值*/
        /*用最大堆中最后一个元素从根结点开始向上过滤下层结点*/
    temp = H- > Elements[H->Size--] ;
    for( Parent=1; Parent*2<=H->Size; Parent=Child ) {
        Child = Parent ★2 ;
        if( (Child!= H->Size)&&(H->Elements [Chi1d] < H->Elements [Chi1d+1]) )
            Child++; /* Child指向左右子结点的较大者*/
        if( temp >= H-> Elements [Chi1d] ) break ;
        else /*移动temp元素到下一层*/
            H->Elements [Parent] = H->Elements [Child] ;
    }
    H->Elements [Parent] = temp ; 
    return MaxItem :
}

4，最大堆的建立：

建立最大堆:将已经存在的N个元素按最大堆的要求存放在一个一维数组中

方法1: 通过插入操作，将N个元素一个个相继插入到一个初始为空的堆中去，其时间代价最大为O(N logN)。
方法2:在线性时间复杂度下建立最大堆。
(1)将N个元素按输入顺序存入，先满足完全二叉树的结构特性
(2)调整各结点位置，以满足最大堆的有序特性。

哈夫曼树与哈夫曼编码

一，哈夫曼树的定义

带权路径长度(WPL):设二叉树有n个叶子结点，每个叶子结点带有权值Wk;从根结点到每个叶子结点的长度为Ik,则每个叶子结点的带权路径长度之和就是:

最优二叉树或哈夫曼树: WPL最小的二叉树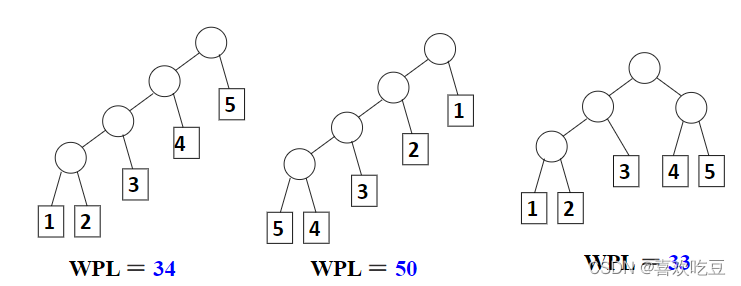

二，哈夫曼树的构造

每次把权值最小的两棵子树合并

typedef struct TreeNode * Huf fmanTree ;
struct TreeNode {
    int Weight;
    HuffmanTree Left, Right;
}
Huf fmanTree Huffman( MinHeap H )
{     /*假设H->Size个权值已经存在H->Elements []->Weight里*/
    inti;
    Huf fmanTree T ;
    BuildMinHeap(H) ; /*将H->Elements []按权值调整为最小堆*/
    for(i = 1; i < H->Size; i++) { /*做H->Size-1次合并*/
        T = malloc( sizeof( struct TreeNode) ) ; /*建立新结点*/
        T->Left = DeleteMin(H) ;
            /*从最小堆中删除-一个结点， 作为新T的左子结点*/
        T->Right = DeleteMin(H) ;
            /*从最小堆中删除-一个结点，作为新T的右子结点*/
        T->Weight = T->Left->Weight+T->Right->Weight ;
            /*计算新权值*/
        Insert( H，T ) ; /*将新T插入最小堆*/
    }
    T =DeleteMin(H) ;
        //整体复杂度为O(N logN)
    returnT;
}

三，哈夫曼树的特点

没有度为1的结点;
n个叶子结点的哈夫曼树共有2n-1个结点;
哈夫曼树的任意非叶节点的左右子树交换后仍是哈夫曼树;
对同一组权值{w1 ,W2, .... wn}，是否存在不同构的两
棵哈夫曼树呢?
对一组权值{1,2,3,3}，不同构的两棵哈夫曼树: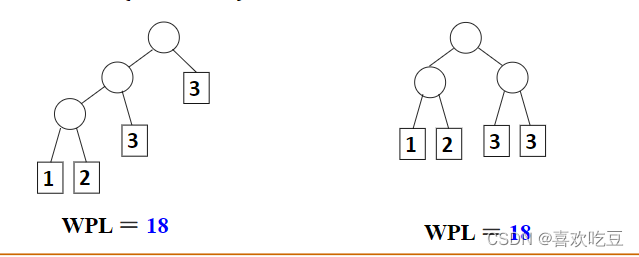

四，哈夫曼编码

给定一段字符串，如何对字符进行编码，可以使得该字符串的编码存储空间最少?

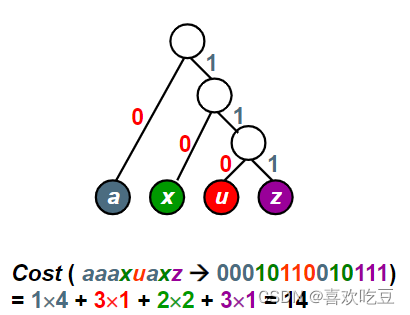
[例]假设有一段文本，包含58个字符，并由以下7个字符构: a, e, i,s, t,空格(sp)，换行(nl) ;这7个字符出现的次数不同。如何对这7个字符进行编码，使得总编码空间最少?

[分析]
(1)用等长ASCII编码: 58 X8 = 464位;
(2)用等长3位编码: 58 X3= 174位;
(3)不等长编码:出现频率高的字符用的编码短些，出现频率低的字符则可以编码长些?

怎么进行不等长编码?
如何避免二义性?
⑨前缀码prefix code:任何字符的编码都不是另一字符编码的前缀
◆可以无二义地解码

二叉树用于编码
用二叉树进行编码:
(1)左右分支: 0、1
(2)字符只在叶结点上