本篇博客预备知识：
线性回归 最小二乘法的求解推导与基于Python的底层代码实现
线性回归 特征扩展的原理与python代码的实现

1 正则项的含义

在线性回归中，正则项是一种用于控制模型复杂度的技术，它通过将系数的大小加入到损失函数中，以限制模型的复杂度。在线性回归中，通常使用L1正则项或L2正则项。正则项的形式可以表示为：

L1正则项（Lasso）：

$$L_1=\lambda \sum _{i=1}^p\left|w_i\right|$$

L2正则项（Ridge）：

$$L_2=\lambda \sum _{i=1}^p{w}_i^2$$

其中，$p$是系数的数量，$w_i$是第$i$个系数，$\lambda$是正则化参数，用于控制正则化的强度。

L1正则项将系数的绝对值之和作为正则化项，可以促使模型中的某些系数变为0，从而实现特征选择的效果。这意味着，L1正则项可以在模型中选择最重要的特征，从而提高模型的泛化能力。

L2正则项将系数的平方和作为正则化项，可以防止模型中的系数过大，从而减少模型的过拟合。L2正则项在许多机器学习任务中都被广泛使用。

以L2正则项为例，加入正则项前，损失函数为：$$J(w)=\frac{1}{2m}\sum _{i=1}^m{\left(h_w(x^{(i)})-y^{(i)}\right)}^2$$
加入正则项后，损失函数变为:$$J(w)=\frac{1}{2m}\sum _{i=1}^m{\left(h_w(x^{(i)})-y^{(i)}\right)}^2+\frac{\lambda }{2m}\sum _{j=1}^n{w}_j^2$$
其中，$h_w(x^{(i)})$是预测值，$y^{(i)}$是实际值，$w_j$是第$j$个特征的权重，$\lambda$是正则化参数，用于控制正则化的强度。

这就意味着，在模型拟合中，将会寻找模型在训练集的表现与模型复杂度之中的平衡点。在实践中，通常使用交叉验证来选择最佳的正则化参数$\lambda$，以获得最好的性能和泛化能力。正则项是一种非常有效的技术，可以帮助解决过拟合问题，并提高模型的泛化能力。

2 L1与L2正则项的区别

除了前面提到的L1与L2在算法上的区别之外，还有一个重要的区别在于L1正则项的解不是唯一的，而L2正则项的解是唯一的。这是由于L1正则项的正则化图形是一个菱形，其边界在坐标轴上，而L2正则项的正则化图形是一个圆形，其边界是一个平滑的曲线。这个区别使得L1正则项的解在特定情况下可能不是唯一的。具体见下图：

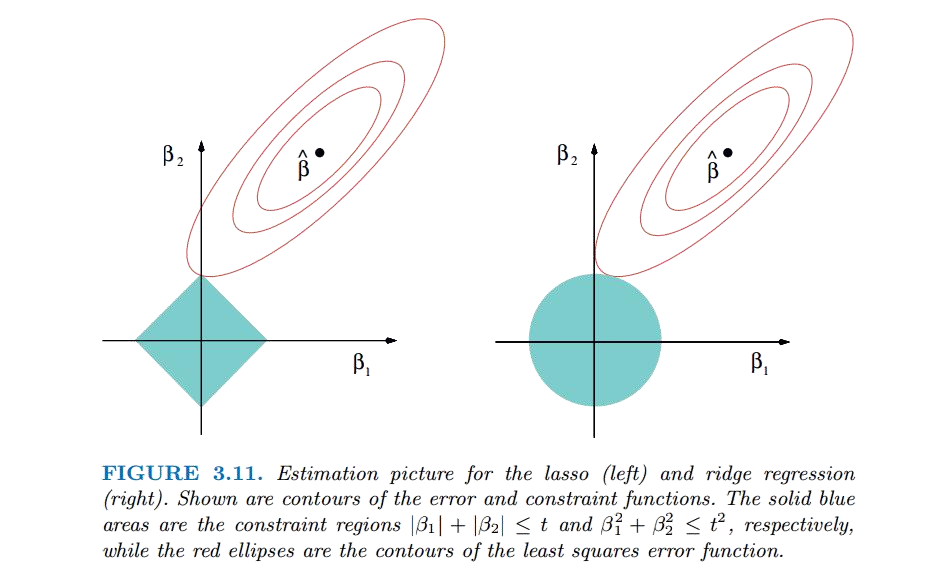
同时，这一图片也解释了为什么L1正则可以在模型中选择最重要的特征，因其交点更容易出现在坐标轴上，而坐标轴上的点意味着某个$\theta$变为了0。

通常情况下很难说L1和L2正则哪个更好，因此出现了Elastic Net正则化技术，即把L1正则和L2正则结合起来。

Elastic Net的正则化项可以表示为：

$$L_{1,2}={\lambda }_1\sum _{i=1}^p\left|w_i\right|+{\lambda }_2\sum _{i=1}^p{w}_i^2$$

其中，${\lambda }_1$和${\lambda }_2$分别是L1正则项和L2正则项的正则化参数，$p$是系数的数量，$w_i$是第$i$个系数。

Elastic Net的主要优点是可以克服L1和L2正则项各自的缺点，并同时利用它们的优点。通过调整L1和L2正则项的权重，可以控制特征选择和平滑效果之间的权衡，从而实现更好的性能和泛化能力。

3 正则的python实现

3.1 Lasso 正则

使用from sklearn.linear_model import Lasso即可导入Lasso回归的包，之后的建模顺序如下：

1. 导入所需的库和数据（这里和上篇博客一样，也是用波士顿房价）

from sklearn.linear_model import Lasso
from sklearn.datasets import load_boston
boston = load_boston()
X = boston.data
y = boston.target

2. 创建Lasso模型对象

lasso = Lasso(alpha=1.0)

3. 拟合模型

lasso.fit(X, y)

4. 访问模型的系数

print(lasso.coef_)

5. 预测

y_pred = lasso.predict(X)

6. 模型性能评价

from sklearn.metrics import r2_score
print(r2_score(y, y_pred))

这段函数的输出为：

可以看到，部分$\theta$的值为0，加入Lasso正则化成功的起到了特征筛选的作用。

3.2 Ridge正则

在python中使用from sklearn.linear_model import Ridge即可使用Ridge回归，之后的模型训练与使用与Lasso完全相同，非常的简单，这里就不重复讲解。
同样使用波士顿数据集，Ridge正则的代码结果为：

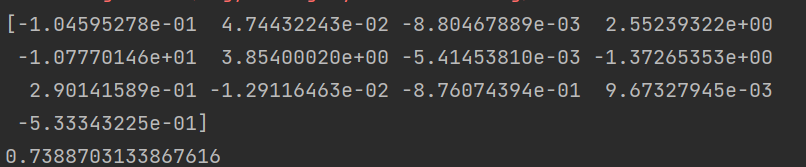
可以看到，这次的$\theta$不再有零值了，但是不重要的特征所对应的$\theta$变得非常小。起到了前面所说的防止模型中的系数过大，从而减少模型的过拟合作用。

3.3 Elastic Net正则

在python中使用from sklearn.linear_model import ElasticNet即可使用Elastic Net回归。与前面两个方法1相比，在创建类市Elastic Net多了一个接收参数：

elastic_net = ElasticNet(alpha=1.0, l1_ratio=0.5)

L1_ratio参数控制L1正则化和L2正则化之间的权重，取值在0-1之间。取1即等同于Lasso，取0等同于Ridge。其他部分的方法与上面也完全一致。

4 案例实例

下面我们使用波士顿房价数据集进行对比三种正则的表现。
首先，我们导入数据，并对数据进行二阶多项式扩展。这里二项式扩展一是为了复习上一篇博客的内容，二是为了模拟日常项目中遇到的无用特征过多的情况。

import numpy as np  
from sklearn.datasets import load_boston  
from sklearn.preprocessing import PolynomialFeatures  
from sklearn.linear_model import LinearRegression, Lasso, Ridge, ElasticNet  
from sklearn.model_selection import cross_val_score, KFold  
  
# 加载波士顿房价数据集  
boston = load_boston()  
X = boston.data  
y = boston.target  
  
# 进行2阶多项式扩展  
poly = PolynomialFeatures(degree=2, include_bias=False)  
X_poly = poly.fit_transform(X)

随后，分别定义定义LinearRegression、Lasso、Ridge、ElasticNet模型。这里Ridge回归的惩罚系数给的非常高，远高于另外两种模型。这是因为博主对这个数据集已经进行过尝试，找到了合适的超参范围。实际项目中，建议根据实际情况进行网格搜索（GridSearch）。

# 定义LinearRegression、Lasso、Ridge、ElasticNet模型  
lr = LinearRegression()  
lasso = Lasso(alpha=1.0)  
ridge = Ridge(alpha=100.0)  
elastic_net = ElasticNet()

为了对模型的评价更加客观，我们使用5折交叉验证，评估模型的表现。

# 定义5折交叉验证  
cv = KFold(n_splits=5, shuffle=True, random_state=1)  
  
# 使用交叉验证评估模型性能  
scores_lr = cross_val_score(lr, X_poly, y, scoring='r2', cv=cv)  
scores_lasso = cross_val_score(lasso, X_poly, y, scoring='r2', cv=cv)  
scores_ridge = cross_val_score(ridge, X_poly, y, scoring='r2', cv=cv)  
scores_elastic_net = cross_val_score(elastic_net, X_poly, y, scoring='r2', cv=cv)

最后，计算并输出每个模型的分数，选择最佳的模型。

# 计算交叉验证的R平方分数  
r2_lr = np.mean(scores_lr)  
r2_lasso = np.mean(scores_lasso)  
r2_ridge = np.mean(scores_ridge)  
r2_elastic_net = np.mean(scores_elastic_net)  
  
# 输出每个模型的R平方分数  
print('Linear Regression R2:', r2_lr)  
print('Lasso R2:', r2_lasso)  
print('Ridge R2:', r2_ridge)  
print('ElasticNet R2:', r2_elastic_net)

这段代码的整体输出结果为：

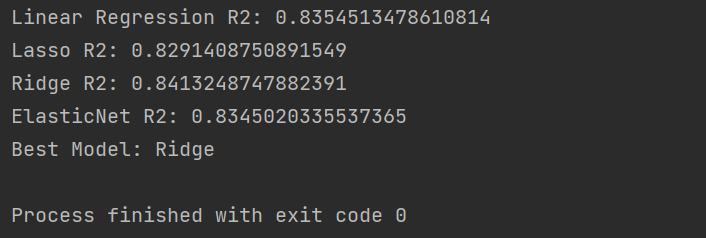
可以看到各个模型的表现相差不大。这主要是因为波士顿数据集量足够且相对规范，各个模型的表现均较为良好。同时，我们也没有选择各个模型的最佳超参数。

最后提醒大家，如果需要使用模型的话，需要将最佳的模型与超参数取出，重新训练。因为在cv过程中，我们得到了5个模型，无法判断那个最佳，最好是使用全部数据集再训练一次。

点此可免费下载这篇文章的完整代码