二阶常微分方程的数值解法（中心差分法和有限体积法）

这里我们介绍中心差分法和有限体积法求解方程。
题目：
用差分法的中心差分格式和有限体积法求解两点边值问题
$u^{\prime \prime }-\alpha \left(2x-1\right)u^{\prime }-2\alpha u=0,0<x<1u\left(0\right)=u\left(1\right)=1,$
其中，参数$\alpha =10$，得到不同网格最大误差和收敛阶。

问题分析

Step 1：网格剖分：首先取 N + 1 个节点为： $a=x_0<x_1<x_2<\cdots <x_N=b$,
将区间 [a,b] 作等距剖分，划分为 N 个小区间,记 $h=x_{i+1}-x_i,i=1,2,\cdots ,N-1$为网格步长.再进行对偶剖分：取相邻节点 $x_{i+1},x_i$ 的中点$x_{i+\frac{1}{2}}=\frac{1}{2}\left(x_{i+1}-x_i\right),i=1,2,\cdots ,N-1.$由这些节点构成的剖分为对偶剖分.
(i)中心差分法：
$\frac{1}{h^2}\left(u_{i+1}-2u_i+u_{i-1}\right)-\frac{\alpha \left(2x_i-1\right)}{2h}\left(u_{i+1}-u_{i-1}\right)-2\alpha u_i=0$
$\Rightarrow$
$\left(\frac{1}{h^2}-r_i\right)u_{i+1}+\left(-\frac{2}{h^2}-2\alpha \right)u_i+\left(\frac{1}{h^2}+r_i\right)u_{i-1}=0$,

where $r_i=\frac{\alpha \left(2x_i-1\right)}{2h}.$
Let $A=\left[\begin{array}{cccccc}-\frac{2}{h^2}-2\alpha & \frac{1}{h^2}-r_1& 0& \cdots & 0& 0\\ \frac{1}{h^2}+r_2& -\frac{2}{h^2}-2\alpha & \frac{1}{h^2}-r_2& \cdots & 0& 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& 0& 0& \cdots & \frac{1}{h^2}+r_{N-1}& -\frac{2}{h^2}-2\alpha \end{array}\right],$
$$\begin{gathered} U={\left(u_1,u_2,\cdots ,u_{N-1}\right)}^T, \\ b={\left(-u_0\left(\frac{1}{h^2}+r_1\right),0,0,\cdots ,0,-u_N\left(\frac{1}{h^2}+r_{N-1}\right)\right)}^T \end{gathered}$$.
Then AU=b.
接着解出U即可.

(ii)有限体积法：
Let $W\left(x\right)=\frac{du}{dx}$, then $\frac{dW}{dx}-\alpha \left(2x-1\right)W\left(x\right)-2\alpha u=0.$
两边同时积分得：
$W(x_{i+\frac{1}{2}})-W(x_{i-\frac{1}{2}})-{\int }_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\alpha (2x-1)W(x)dx-{\int }_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}2\alpha udx=0.$
运用积分中值定理可得：
$W(x_{i+\frac{1}{2}})-W(x_{i-\frac{1}{2}})-W(x_i){\int }_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\alpha (2x-1)dx-u_i{\int }_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}2\alpha dx=0.$
$\Rightarrow$
$W(x_{i+\frac{1}{2}})-W(x_{i-\frac{1}{2}})-W(x_i)(x_{i+\frac{1}{2}}+x_{i-\frac{1}{2}}-1)h\alpha -2\alpha u_{i}h=0$
$\Rightarrow$
$\frac{1}{h}\left(u_{i+1}-2u_i+u_{i-1}\right)-\frac{\alpha }{4}\left(x_{i+1}+2x_i+x_{i-1}\right)\left(u_{i+1}-u_{i-1}\right)+\frac{\alpha }{2}\left(u_{i+1}-u_{i-1}\right)-{2\alpha u}_{i}h=0$
$\Rightarrow$
$\left(\frac{1}{h}-l_i+\frac{\alpha }{2}\right)u_{i+1}+\left(-\frac{2}{h}-2\alpha h\right)u_i+\left(\frac{1}{h}+l_i-\frac{\alpha }{2}\right)u_{i-1}=0,$
where$l_i=\frac{\alpha }{4}\left(x_{i+1}+2x_i+x_{i-1}\right)$.
Let $A=\left[\begin{array}{cccccc}-\frac{2}{h}-2\alpha h& \frac{1}{h}-l_1+\frac{\alpha }{2}& 0& \cdots & 0& 0\\ \frac{1}{h}+l_2-\frac{\alpha }{2}& -\frac{2}{h}-2\alpha h& \frac{1}{h}-l_2+\frac{\alpha }{2}& \cdots & 0& 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& 0& 0& \cdots & \frac{1}{h}+l_{N-1}-\frac{\alpha }{2}& -\frac{2}{h}-2\alpha h\end{array}\right],$

$U={\left(u_1,u_1,\cdots ,u_{N-1}\right)}^T,F={\left(-u_0\left(\frac{1}{h}+l_1-\frac{\alpha }{2}\right),0,0,\cdots ,0,-u_N\left(\frac{1}{h}-l_{N-1}+\frac{\alpha }{2}\right)\right)}^T$
Then AU=F.
接着解出U即可.

全部代码如下(matlab)

function E=Centered(h)%中心差分法
u0=1;
uN=1;
N=1/h;
x=zeros(1,N+1);
for i=1:(N)
    x(i+1)=x(i)+h;
end
R=zeros(1,N+1);
for i=1:(N+1)
    R(i)=10*(2*x(i)-1)/(2*h);
end
A=zeros(N-1,N-1);
A(1,1)=-2/(h*h)-20;
A(1,2)=1/(h*h)-R(2);
A(N-1,N-1)=-2/(h*h)-20;
A(N-1,N-2)=1/(h*h)+R(N)
for i=2:(N-2)
        A(i,i)=-2/(h*h)-20;
        A(i,i+1)=1/(h*h)-R(i+1);
        A(i,i-1)=1/(h*h)+R(i+1);
end
b=zeros(1,N-1);
b(1)=-u0*(1/(h*h)+R(2));
b(N-1)=-uN*(1/(h*h)-R(N));
y=A\b';
Y=zeros(N+1,1);
Y(1,1)=1;
Y(N+1,1)=1;
for i=2:N
    Y(i,1)=y(i-1,1);
end
plot(x,Y ,'r*-');
hold on;
exa = dsolve('D2u = 10*(2*x-1)*Du+20*u', 'u(0)=1','u(1)=1', 'x');       %求出解析解
ezplot(exa, [0,1]);       %画出解析解的图像
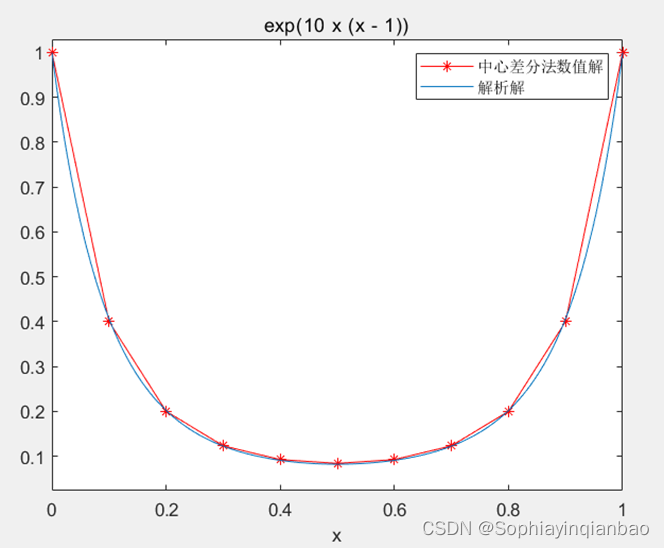
legend('中心差分法数值解','解析解' );
u=zeros(1,N+1);
exa=inline(exa);
for i=1:(N+1)
    u(i)=feval(exa,x(i));
    e(i)=abs(u(i)-Y(i));
end
E=max(e);

function E=V(h)%有限体积法
u0=1;
uN=1;
N=1/h;
x=zeros(1,N+1);
for i=1:(N)
    x(i+1)=x(i)+h;
end
R=zeros(1,N+1);
for i=2:N
    R(i)=2.5*(x(i+1)+2*x(i)+x(i-1));
end
A=zeros(N-1,N-1);
A(1,1)=-2/h-20*h;
A(1,2)=1/h+5-R(2);
A(N-1,N-1)=-2/h-20*h;
A(N-1,N-2)=1/h-5+R(N);
for i=2:(N-2)
        A(i,i)=-2/h-20*h;
        A(i,i+1)=1/h+5-R(i+1);
        A(i,i-1)=1/h-5+R(i+1);
end
b=zeros(1,N-1);
b(1)=-u0*(1/h-5+R(2));
b(N-1)=-uN*(1/h+5-R(N));
y=A^(-1)*b';
Y=zeros(N+1,1);
Y(1,1)=1;
Y(N+1,1)=1;
for i=2:N
    Y(i,1)=y(i-1,1);
end
plot(x,Y ,'r*-');
hold on;
exa = dsolve('D2u = 10*(2*x-1)*Du+20*u', 'u(0)=1','u(1)=1', 'x');       %求出解析解
ezplot(exa, [0,1]);       %画出解析解的图像
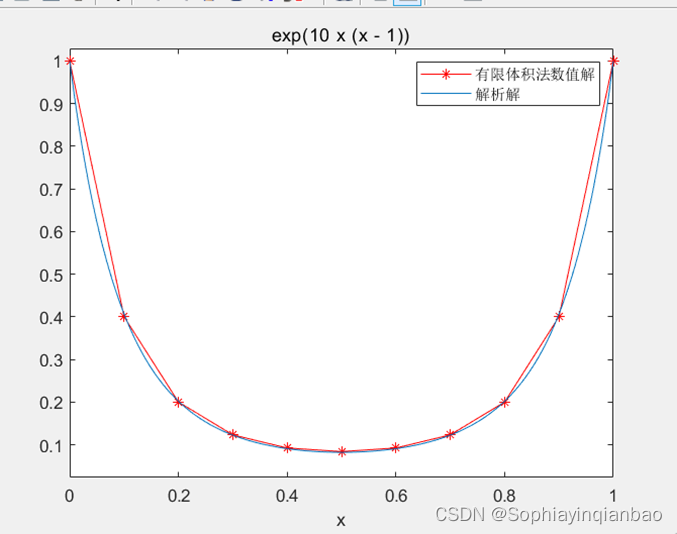
legend('有限体积法数值解','解析解' );
u=zeros(1,N+1);
exa=inline(exa);
for i=1:(N+1)
    u(i)=feval(exa,x(i));
    e(i)=abs(u(i)-Y(i));
end
E=max(e);
%调试
clear all;clc;close  all;
h=[0.1,0.2,0.01,0.02,0.05];
for i=1:5
    E(i)=V(h(i));
    F(i)=Centered(h(i));
end

问题结果

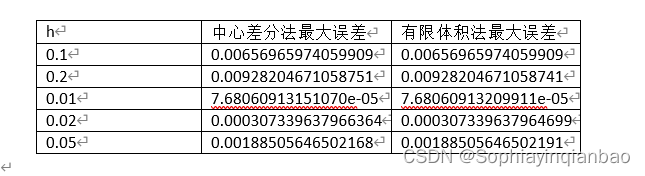
我们发现中心差分法的最大误差与有限体积法的最大误差相差较小，阶数相同，因此我们可以认为中心差分法与有限体积法两者的收敛阶相同，而我们已知中心差分法的收敛阶为2阶，因此有限体积法的收敛阶也是二阶。

（以h=0.1为例，我们画出了两种方法数值解与解析解的图像）