3.1.1动态博弈( dynamic game)

• 序贯博弈( sequential game)
• 参与人集合(N，虚拟参与人，自然的选择的概率分布)
• 参与人的行动顺序(the order of moves)
• 参与人的行动空间(action set)
• 参与人的信息集(information set) :博弈进程方面的信息
• 参与人的支付函数（是所有行动的函数）

【引例】房地产开发博弈

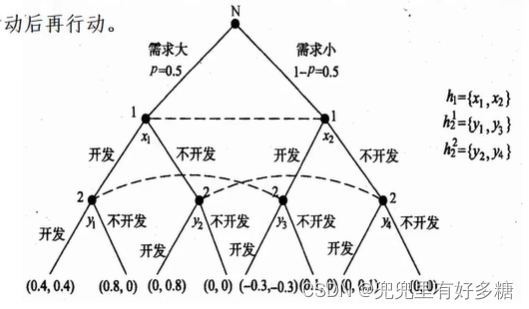
房地产开发商$A,B$正考虑是否要在某地段投资开发一座商住楼，他们面临的选择是开发或不开发。如果开发，就需要投入1亿元资金。假如房地产市场可能出现市场需求大与需求小两种状态，且概率均为0.5。如果市场上同时有两座楼出售，市场需求大时每栋楼售价为1.4亿元，需求小时每栋楼售价为0.7亿元;如果市场上只有一栋楼出售，需求大时售价为1.8亿元，需求小时售价为1.1亿元。试就以下情况画出博弈树并给出参与人的信息集。
(1)$A$首先行动选择开发或不开发，在$A$行动后自然选择市场状态，$B$在观察到$A$的行动和市场需求状况后决定开发或不开发。
(2)$A、B$(参与人1、2）都不知道市场状态，但$A$先行动，$B$在观察到$A$的行动后再行动
【解】
本题中指明A是先进行决策的那一方，B是后进行决策的那一方。可以理解为A一开始进行决策时并没有考察市场，而在A做完决策后，B进行决策的时候，B是调查市场过后的决策。

【引例】

首先参与人1从行动空间$A_1=A,B$中选择行动$a_1$。其次参与人2观察到参与人1的行动后从行动空间$A_2=C,D$中选择行动$a_2$。然后参与人3如果观察到参与人1，2的行动组合$(a_1，a_2)$是$(B,D)$，则他从行动空间$A_{31}=E,F$中选择$a_3$;如果是$(A,C)$或$(A,D)$或$(B,C)$，但参与人3不能分辨，则他从行动空间$A_{32}=L,R$中选择行动$a_3$。
(1)画出博弈树;
(2)写出参与人的信息集。

【解】
(1)

(2)参与人的信息集：
参与人1的信息集;{ $x_1$}
参与人2的信息集;{ $y_1,y_2$}
参与人3的信息集;{ $z_1,z_2,z_3$}{ $z_4$}

【引例】

企业A正在开发某种新产品，其成本有高、低两种可能。A在知道生产过程是高或低成本时，选择是否建新车间。企业B不能观察到A新生产过程的成本高低但可观察到A是否建了新车间。随后，B要决定是否进入该市场与A竞争，如果A的生产过程是高成本，B将会从进入市场获利200万元;但如果A的生产过程是低成本，B进入市场将损失400万元。如果生产过程采用低成本，将增加A利润400万元。如果新生产过程是低成本，则建一个新车间将使A的利润再增加200万元。但如果新生产过程是高成本，则建一个新车间会使A的利润减少400万元。无论新生产过程是高或低成本，也无论A是否建了新车间，B进入市场都会降低A的利润600万元，试画出该博弈的博弈树。

【解】

动态博弈中的基本概念：

• 阶段:动态博弈中参与人的一次行为。
• 路径:从第一阶段到达博弈结束的某个终端各参与人的行为组合。
• 战略:针对每种可能的情况如何选择的完整行动计划。

可信性问题
指动态博弈中先行为的参与人是否该相信后行为的参与人会采取对自己有利或不利的行为。分为“许诺的可信性”和“威胁的可信性”。
子博弈

• 即能够自成一个博弈的某个动态博弈的从其某个阶段开始的后续阶段。
• 必须有一个初始信息集。（前面是怎么到达这个节点的）
• 具备博弈所需要的各种信息。
• 第一个节点不能作为子博弈的初始节点。（也即原博弈不能称为子博弈）

【判断下面两个图各有几个子博弈】

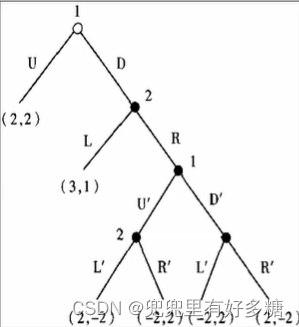
这个图中有且仅有一个子博弈。因为左侧的三个下节点均不能确定其明确的来源，有可能是(U,L)(U,R)或者是(D,L)来的，属于是来源不清楚。而右边的2节点也不能称作子博弈，因为他的去向不明了。所以只有右下角的3节点往下这一个子博弈。

子博弈精炼（完美）纳什均衡
（求解的思路是从子博弈开始分析，精炼是指剔除掉不可信守的威胁或者许诺，并且必须满足纳什均衡的定义）。
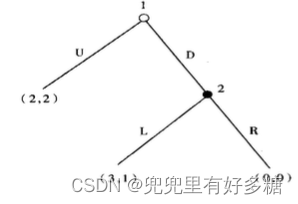
【例题】

【解】
从后往前倒退求纳什均衡解。
先看2选择什么：2选择R的话，得到的是0，选择L得到的是1，所以2一定会倾向选择L。而1选择U的话得到2，选择D的话会到（D，L）结束得到3。因此1会选择D。
所以纳什均衡的最佳战略是（D，L）。
但是如果用静态博弈的方法看纳什均衡，就要列出如下表格：

用划线法确定静态的纳什均衡可以得到两个双划线战略：（U，L）和（D，L）。但是这就是静态博弈的问题所在，因为：如果参与人1选择U，则参与人2的信息集不能达到，即参与人2的信息集不在均衡路径(out of equilibrium path)。所以这两个战略就要被精炼掉，剔除掉。剩余的（D，L）就是子博弈精炼纳什均衡。

动态博弈均衡必须满足:既是纳什均衡，从而具有战略稳定性;又不能包含任何的不会信守的许诺或威胁。
泽尔腾（ 1965):如果动态博弈中各参与人的战略在动态博弈本身和所有子博弈中都构成一个纳什均衡，则称该战略组合为一个“子博弈精练纳什均衡”。

• 方案的完整性
• 个体理性:序贯理性（(sequcntial rationality) 、

逆推归纳法(backward induction) 从动态博弈的最后一个阶段或最后一个子博弈开始，逐步向前倒推以求解动态博弈的方法。

【例题】求该博弈树的子博弈精炼纳什均衡

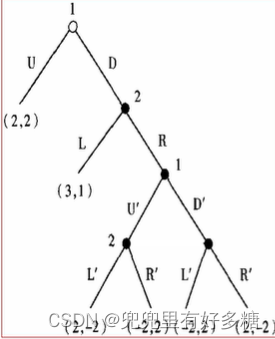
从最后一个阶段开始往前倒退：
最后一个阶段有两个子博弈：（因为这个是参与人2的选择，所以我们的目标是参与人2的收益最大化）左边这个博弈中：参与人2在$L^{\prime }$得到的收益是-2，在$R^{\prime }$中得到的收益是2，所以左边这个博弈我们选择$R^{\prime }$。
对于右边这个博弈：在$L^{\prime }$中获得的收益是2，在$R^{\prime }$中获得的收益是-2。所以右边这个博弈我们选择$L^{\prime }$。

上一个阶段（是参与人1的选择阶段，目标是使得参与人1的收益最大化）：如果参与人1选择$U^{\prime }$，那么会到达（$U^{\prime }$,$R^{\prime }$）,从而得到-2的收益。如果选择$D^{\prime }$，那么会到达（$D^{\prime }$,$L^{\prime }$），然后得到-2的收益。所以这一个阶段对于参与人1来说没有区别。

再往上一个阶段：参与人2选择$L$得到1的收益，选择$R$的话最终会下沉到最后一阶段的博弈，不论从哪里到达他得到的收益都是2。

再往上一个阶段，参与人1选择$U$的话得到2，选择$D$的话最终会下沉到最后一个阶段，从而得到收益为-2.

所以最终的博弈最优解是第一阶段1直接选择$U$，博弈结束。两个人都得到2的收益。

【例题】求该博弈树的子博弈精炼纳什均衡

这个博弈树是没有子博弈的。
因为最后一个子博弈是一个概率事件，就没有办法确定他的确定值，就没有办法往前倒推。
这种情况就得分析$U^{\prime }$和$D^{\prime }$的概率是多少了，然后去分析下面$L^{\prime }$和$R^{\prime }$的期望收益是多少，进而决定是选择哪一个。

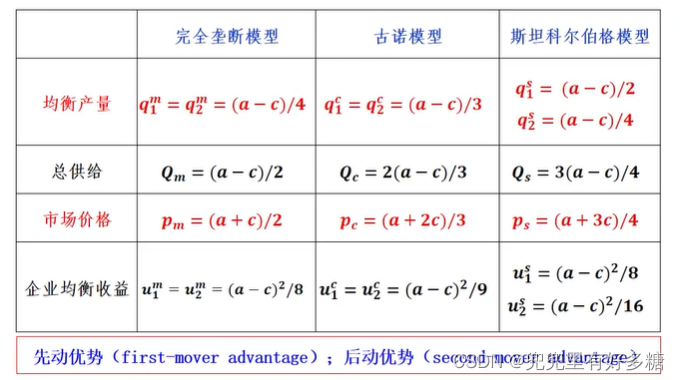
【例题】寡占的斯塔克尔博格模型(Stackelberg，1934)。（行为无限的动态博弈问题）

设两寡头为厂商1和厂商2的战略空间（$q_1、q_2的集合$）都是（$0，Q_{max}$）中的所有实数;厂商1是领头厂商( lcader)，因此他先选择，厂商2是追随企业（follower) ;设价格函数$P=P(Q)=8-Q$（其中$Q=q_1+q_2$，边际生产成本$C_1=C_2=2$，且没有固定成本。
【解】
两厂商的得益函数分别为:
$$u_1=6q_1-q_1^2-q_1{q}_2{u}_2=6q_2-q_2^2-q_1{q}_2$$
但这只是静态博弈的结论。但这里是动态博弈，也就是他们不是同时决策，厂商1决策完的产量和需求会影响到厂商2的决策。
这个动态博弈我们假设就是两个阶段：
第一阶段，厂商1进行决策，然后第二阶段厂商2进行决策。
首先要分析第二阶段厂商2的决策。在$q_1$已经确定的情况下求使$u_2$实现最大值的$q_2$，$q_2$必须满足:
让$u_2$对$q_2$求直接导数，而不是偏导。因为这个阶段$q_1$不是未知数，而是一个已知量，是一个常数。
得到如下式子：
$$u_2=6q_2-q_2^2-q_1{q}_{2}6-2q_2-q_1=0q_2=3-q_1/2$$
厂商1知道厂商2的这种决策思路，他在选择$q_1$时就知道将是根据上式确定的，因此可将上式代入他自己的得益函数，然后再求其最大值。即求使:
将 $q_2=3-q_1/2$带入$u_1=6q_1-q_1^2-q_1{q}_2$中：
$$u_1=6q_1-q_1^2-q_1\left(3-\frac{q_1}{2}\right)=3q_1-\frac{1}{2}{q}_1^2$$
得最大值的$q_1^{\ast }$，令上式对$q_1$的导数为0，可得$q_1^{\ast }=3$。
然后将此结果带入$q_2=3-q_1/2$中求得
$$q_2^{\ast }=3-1.5=1.5$$
双方的得益分别为4.5和2.25。

【例】

两企业进行价格竞争博弈，$p、q$分别是企业1、2的价格。企业1的利润函数是:${\pi }_1=-(p-aq+c{)}^2+q$
企业2的利润函数是:${\pi }_2=-(q-b{)}^3+p$
(1)两个企业同时决策的纳什均衡。
(2)企业1先决策的纳什均衡。
(3)企业2先决策的纳什均衡。
(4)讨论使两个企业都希望自己先决策的参数a、b、c的范围。
【解】
第一小问是静态博弈问题，对各自的反应函数求导然后联立
第二三问是动态博弈问题，先对后决策的进行求导，然后代入。

【例题】设两个参与人之间的三阶段动态博弈如图

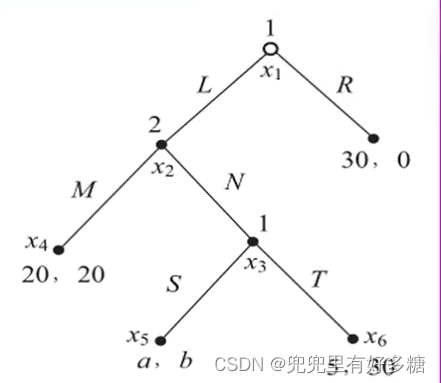
(1)若a和b分别等于10和15，该博弈的子博弈精炼Nash均衡是什么?
(2)x1→x2→x3 →x6是否可能构成该博弈的子博弈精炼Nash均衡路径?为什么?
(3)在什么情况下，博弈的子博弈精炼Nash均衡路径为:x1→x2→x3 →x5 ?
【解】
(1)该博弈的子博弈精炼纳什均衡是$((R,S),M)$（这里表示的是参与人1的所有涉及到他选择时他会进行的最佳选择，实际上的精炼纳什均衡只有一个，就是R）。如果让写出均衡路径就是直接是R。
(2)这条路径不可能构成该博弈的子博弈精炼Nash均衡路径，因为这条路径对应的结构中参与人1的收益5小于参与人1的决策结点x选择R的收益30。
(3)当a >30，b > 20时，博弈的子博弈精炼Nash均衡路径为x1→x2→x3→x5 .

【例题】

假设在Stackellberg模型中两种产品不是同质而是替代的，企业1生产产品1，产品1的边际成本为C1，企业2生产产品2，产品2的边际成本为c2。企业1选择产量q1，企业2选择产量q2。需求函数为:
$$\{\begin{array}{l}{p}_1\left(q_1,q_2\right)=a_1-q_1+k_1{q}_2\\ p_2\left(q_1,q_2\right)=a_2-q_2+k_2{q}_1\end{array}\left(a_1>c_1,a_2>c_2,0\le k_1,k_2\le 1\right)$$
求两个企业的均衡产出数量。
【解】
在该Stackellberg博弈中,两个企业的支付函数为:
$$\{\begin{array}{l}{\pi }_1\left(q_1,q_2\right)=p_1{q}_1-q_1{c}_1=\left(a_1-q_1-k_1{q}_2\right)q_1-q_1{c}_1\\ {\pi }_2\left(q_1,q_2\right)=p_2{q}_2-q_2{c}_2=\left(a_2-q_2-k_2{q}_1\right)q_2-q_2{c}_2\end{array}$$
首先考虑第二阶段，企业2先决策，由②式支付最大化的一阶条件得：
$$\frac{d{\pi }_2}{d{q}_2}=a_2-2q_2-k_2{q}_1-c_2=0\Rightarrow q_2=\frac{a_2-k_2{q}_1-c_2}{2}$$
第一阶段，将后面这个式子带入①式。化简得：
$${\pi }_1=\left(a_1-\frac{2q_1-k_1{k}_2{q}_1-k_1{c}_2+k_1{a}_2}{2}\right)q_1-q_1{c}_1$$
由上式的一阶条件得：
$$\begin{array}{rl}& \frac{d{\pi }_1}{d{q}_1}=a_1-\frac{4q_1-2k_1{k}_2{q}_1-k_1{c}_2+k_1{a}_2}{2}-c_1=0\\ & \Rightarrow q_1^{\ast }=\frac{2\left(a_1-c_1\right)+k_1\left(c_2-a_2\right)}{4-2k_1{k}_2}\end{array}$$
于是将上式带入③式：
$$q_2^{\ast }=\frac{\left(4-k_1{k}_2\right)\left(a_2-c_2\right)-2k_2\left(a_1-c_1\right)}{8-4k_1{k}_2}$$
由⑤⑥式得该问题的子博弈精炼纳什均衡为：
$$\left\{\frac{2\left(a_1-c_1\right)+k_1\left(c_2-a_2\right)}{4-2k_1{k}_2},\frac{\left(4-k_1{k}_2\right)\left(a_2-c_2\right)-2k_2\left(a_1-c_1\right)}{8-4k_1{k}_2}\right\}$$

【例题】

有两人就如何分割1万元进行谈判，并且已经定下了这样的规则:首先由甲提出一个分割比例，对此，乙可以接受也可以拒绝;如果乙拒绝甲的方案，则他自己应提出另一个方案，让甲选择接受与否。如此循环。在上述循环过程中，只要有任何一方接受对方的方案博弈就告结束，而如果方案被拒绝，则被拒绝的方案就与以后的讨价还价过程不再有关系。每次一方提出一个方案和另一方选择是否接受为一个阶段。再假设讨价还价每多进行一个阶段，由于谈判费用和利息损失等，双方的得益都要打一次折扣，折扣率称为消耗系数。如果限制讨价还价最多只能进行三个阶段，到第三阶段乙必须接受甲的方案，则称为三阶段的讨价还价博弈。(bargaining game of alternating offers)
【解】

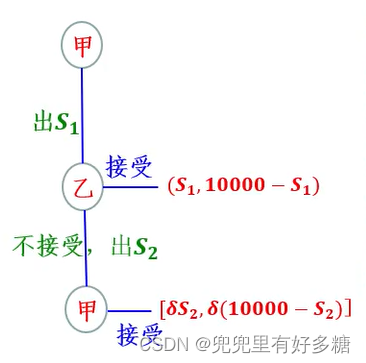
第一阶段，甲的方案是自己得$S_1$,乙得$10000-S_1$,乙可以选择接受或不接受，接受则双方得益分别为见和$10000-S_1$，谈判结束，如果已不接受，则开始下一阶段;
第二阶段，乙的方案是甲得$S_2$，自己得$10000-S_2$，由甲选择是否接受，接受则双方得益分别为$\delta S_2$和$\delta (10000-S_2)$，谈判结束，如甲不接受则进行下一阶段;
第三阶段,甲提出自己得$S$，乙得$10000—S$，这时乙必须接受，双方得益为${\delta }^{2}S$和${\delta }^2(10000-S)$。

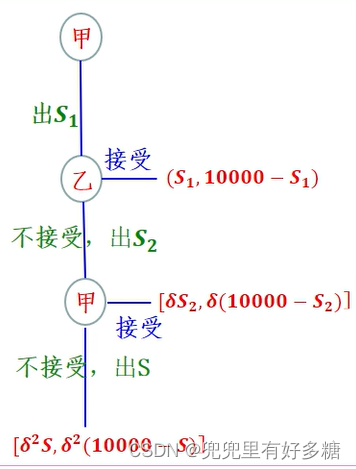
那么我们从第三阶段开始分析：
第三阶段，甲得${\delta }^{2}S$,乙得$(10000-S){\delta }^2$

我们想要得到我们自己想得到的，那么我们提出方案的时候首先要满足对方的要求，你的方案才有可能实现。所以提出方案的时候就是先满足对方想要的，然后在这个基础上实现自己的利益的最大化。
那么问题在于我们如何让他接收我们的方案呢，那就是我们的方案中我们给他的利益不能少于他拒绝过后他自己的得益。
所以我们自己提出的方案能不能实现取决于对方接不接受，而对方接不接受取决于他接受过后的收益值不能小于他拒绝过后他自己提出的收益值。

第二阶段，$\delta S_2$应该满足不小于${\delta }^{2}S$，那么我们为了满足我们的利益最大化，此处取等于即可，也就是以最低要求满足他。$\delta S_2={\delta }^{2}S$,此时乙得$\delta (10000-S\delta )>{\delta }^2(10000-S)$,也就是我们提出的这个方案中我们自己得到的比他拒绝过后他给我们的利益要高，并且也满足了他拒绝过后他要求的利益，所以这个方案才能实现。
第一阶段，$S_1$应满足$10000-S_1=\delta (10000-\delta S)$,即$S_1=10000-10000\delta +{\delta }^{2}S$，此时甲得收益为$S_1=10000-10000\delta +{\delta }^{2}S>{\delta }^{2}S$

若把上述第三回合理解成从第一阶段开始的无限回合博弈的第三回合，则由于甲在第三回合的出价是最终出价，因此这个无限回合博弈相当于一个前面讨论过的，甲在第三回合的出价有强制力的三回合讨价还价博弈。根据前面对三回合讨价还价博弈的逆推归纳法的结论可知，该博弈的解是甲在第一回合出价:
$S_1=10000-10000\delta +{\delta }^{2}S$
$S=S_1=10000-10000\delta +{\delta }^{2}S$
$S^{\ast }=\frac{10000}{1+\delta }$
$10000-S^{\ast }=\frac{10000\delta }{1+\delta }$

【例题】关税和不完全国际竞争

设国家1和国家2确定对进口商品征收关税的税率，两国各有一个企业(企业1和企业2）生产既内销又出口的相互竞争的商品，消费者在各自的国内市场上购买国货或进口货。首先由两国政府同时制订关税率$t_1$和$t_2$﹔然后企业1和企业2根据$t_1$和$t_2$同时决定各自的内销和出口产量$(h_1,e_1)$和$(h_2,e_2)$。两企业的边际生产成本同为常数C且都无固定成本。市场出清价格$P=a-Q$($Q$为国内市场上的商品总量）。

【解】
本题参与人一共有四个（两个国家，两个企业）。
动态博弈不是每个阶段只能有一个人行动，他的每个阶段也可以有多个人同时进行静态博弈。

先从第二阶段开始：
假设两国已经选择关税率分别为$t_1$和$t_2$，则如果$(h_i^{\ast },e_i^{\ast })$是在设定$t_1$和$t_2$情况下两个企业之间的一个纳什均衡，那么$(h_i^{\ast },h_j^{\ast },e_i^{\ast },e_j^{\ast })$必须是满足下述最大值问题的解：${\max }_{h_i,e_i\ge 0}\left({\mathbf{t}}_{\mathbf{i}},{\mathbf{t}}_{\mathbf{j}},{\mathbf{h}}_{\mathbf{i}},{\mathbf{h}}_{\mathbf{j}}^{\ast },{\mathbf{e}}_{\mathbf{i}},{\mathbf{e}}_{\mathbf{j}}^{\ast }\right)$
$$\begin{array}{rl}& {\pi }_i\left(t_i,t_j,h_i,h_j,e_i,e_j\right)=P_i{h}_i+P_j{e}_i-c\left(h_i+e_i\right)-t_j{e}_i\\ & =\left[a-\left(h_i+e_i\right)\right]h_i+\left[a-\left(h_j+e_i\right)\right]e_i-c\left(h_i+e_i\right)-t_j{e}_i\end{array}$$
上述最大值问题就可分解为：
max ⁡ h i ≥ 0 { h i [ a − ( h i − e j ∗ ) − c ] } max ⁡ e i ≥ 0 { e i [ a − ( e i − h ∗ j ) − c ] − t j e i } \max _{h_i \geq 0}\left\{h_i\left[a-\left(h_i-e_j^*\right)-c\right]\right\} \quad \max _{e_i \geq 0}\left\{e_i\left[a-\left(e_i-h^*{ }_j\right)-c\right]-t_j e_i\right\} hi​≥0max​{ hi​[a−(hi​−ej∗​)−c]}ei​≥0max​{ ei​[a−(ei​−h∗j​)−c]−tj​ei​}
此时有两个决策变量：国内生产多少，国外出口多少。
$$\begin{array}{rl}& h_i^{\ast }=\frac{1}{2}\left(a-e_j^{\ast }-c\right)e_i^{\ast }=\frac{1}{2}\left(a-h^{\ast }{}_j-c-t_j\right)\\ & h_i^{\ast }=\frac{a-c+t_i}{3}{e}_i^{\ast }=\frac{a-c-2t_j}{3}\end{array}$$
回到第一阶段：两国家同时进行$t_1$和$t_2$的决策
$$\begin{array}{c}{w}_i=w_i\left(t_i,t_j,h_i,h_j,e_i,e_j\right)=\frac{1}{2}{\left(h_i+e_j\right)}^2+{\pi }_i+t_i{e}_j\\ w_i\left(t_i,t^{\ast }{}_j\right)=\frac{{\left[2(a-c)-t_i\right]}^2}{18}+\frac{{\left(a-c+t_i\right)}^2}{9}+\frac{{\left(a-c-2t_j^{\ast }\right)}^2}{9}+\frac{t_i\left(a-c-2t_j^{\ast }\right)}{3}\\ t^{\ast }{}_i=\frac{a-c}{3},i=1,2h_i^{\ast }=\frac{4(a-c)}{9}{e}_i^{\ast }=\frac{a-c}{9}\end{array}$$

【例题】

【例题】劳资谈判

设厂商的利润是内部信息，工会只知道其标准分布于区间[0，1]上。工人不被该厂商雇佣就会失去全部收入，即收入为0;设厂商和工会的讨价还价最多只能进行两个回合，每个回合都是先由工会提出工资要求，由厂商选择是否接受。如果第一个回合厂商就接受工会的工资要求则博弈结束，否则开始第二个回合。若第二个回合厂商不接受则表示厂商不雇佣工会的工人了;如果协议在第二个回合达成，则双方得益都要打折扣。

【解】
（先上结果）该博弈的唯一的完美贝叶斯均衡

• 工会第一回合要求工资：

$$W_1^{\ast }=\frac{(2-\delta {)}^2}{2(4-3\delta )}$$

• 如果厂商的利润超过${\pi }_1^{\ast }=\frac{2-\delta }{4-3\delta }$，则厂商接收$W_1^{\ast }$，否则拒绝$W_1^{\ast }$。
• 如果第一回合工资被拒绝，工会将对厂商利润的判断修改为标准分布于$[0,{\pi }_1^{\ast }]$。第二回合要求工资

$$W_2^{\ast }=\frac{{\pi }_1^{\ast }}{2}=\frac{2-\delta }{2(4-3\delta )}$$

• 如果厂商的利润超过$W_2^{\ast }$,则接受该工资要求，否则仍然拒绝。

先看第二回合：
厂商的选择：只要$\pi >=W_2^{\ast }$，选择接受，得益是：$\delta (\pi -W_2^{\ast })$。
工会的选择：$ma{x}_{w_2}(W_2\times p_{2a}+0\times p_{2r})$
p 2 a = p { π ≥ W 2 } = ( π 1 − W 2 ) / π 1 p 2 r = p { π < W 2 } = W 2 / π 1 max ⁡ W 2 [ W 2 ( π 1 − W 2 π 1 ) ] \begin{aligned} &\begin{aligned} & p_{2 a}=p\left\{\pi \geq W_2\right\}=\left(\pi_1-W_2\right) / \pi_1 \\ & p_{2 r}=p\left\{\pi<W_2\right\}=W_2 / \pi_1 \end{aligned}\\ &\max _{W_2}\left[W_2\left(\frac{\pi_1-W_2}{\pi_1}\right)\right] \end{aligned} ​​p2a​=p{ π≥W2​}=(π1​−W2​)/π1​p2r​=p{ π<W2​}=W2​/π1​​W2​max​[W2​(π1​π1​−W2​​)]​

在没有进行第一回合的时候，工会对厂商的利润分布水平的预估是$[0,1]$这个范围，但是在一回合结束之后厂商还没有同意，那么工会就了解到厂商的利润水平没有那么高，就会对预估进行调整。
上式中的${\pi }_1$是第一回合厂商没有接受工会的要求之后，工会对厂商的利润区间做的重新估计，就是估计为$[0,{\pi }_1]$。
所以第二回合工会就会在这个区间内提出工资水平。而因为这都是均匀分布的，所以线段的长度就等于相应的概率。
所以计算第二回合工会被接受的概率，就是计算厂商的利润水平大于工会工资的那一部分长度，就是${\pi }_1-W_2$，然后除以总长度$\pi$就是概率。

因此，工会的最佳选择就是对上式求$W_2$的偏导数并令其为0，则可以求得：$W_2^{\ast }={\pi }_1/2$
如果进行到第二回合，并且厂商接受要求，则双方得益为：
工会：$\delta {\pi }_1/2$,厂商：$\delta (\pi -{\pi }_1/2)$

回到第一回合：
本回合厂商选择接收的条件：$\pi -W_1^{\ast }>=\delta (\pi -{\pi }_1/2)$

意思是这个这个阶段的利润$\pi$减去工资支出$W_1^{\ast }$之后得出的得益不小于“这一阶段拒绝过后在第二阶段得到的收益。

整理可得：$$\pi \ge \frac{W_1^{\ast }-\delta {\pi }_1/2}{1-\delta }$$
令：
$${\pi }_1=\frac{W_1^{\ast }-\delta {\pi }_1/2}{1-\delta }则整理过后得：{\pi }_1=\frac{2W_1^{\ast }}{2-\delta }$$
工会所选择的工资$W_1^{\ast }$使得自己的期望得益最大，即满足：
$ma{x}_{w_1}[W_1\times p_{1a}+\delta W_2(W_1)\times p_{ra}]$
（这一阶段被接受的概率乘上这一阶段的工资收益，加上：这一阶段被拒绝但是下一阶段被接受的概率乘上下一阶段的工资收益乘折现率）

如图：第一阶段提出的工资被接受的概率是提出$W_1$这样的工资之后厂商发现自己的利润${\pi }_1$大于$W_1$，所以也就是${\pi }_1$在$[W_1,1]$之间。所以也可以称$W_1$为${\pi }_1$。其区间长度就是$1-{\pi }_1$，概率就是$\frac{1-{\pi }_1}{1}$。

所以可以得到被接受的概率：
$$p_{1a}=\frac{1-{\pi }_1}{1}=1-\frac{2W_1}{2-\delta }=\frac{2-\delta -2W_1}{2-\delta }$$
从而可以得到被拒绝的概率$p_{1r}$
$$p_{ra}=p_{1r}\times p_{2a}=\frac{2W_1}{2-\delta }\times \frac{{\pi }_1-W_2}{{\pi }_1}=\frac{2{\pi }_1}{2-\delta }\times \frac{{\pi }_1-{\pi }_1/2}{{\pi }_1}=\frac{W_1}{2-\delta }$$
从而可以得到工会的支付函数是：
$$\underset{w_1}{\max }\left[W_1\times \frac{2-\delta -2W_1}{2-\delta }+\delta \frac{W_1}{2-\delta }\times \frac{W_1}{2-\delta }\right]$$
求其对$W_1$的一阶微分让其为0可以得到：
$$W_1^{\ast }=\frac{(2-\delta {)}^2}{2(4-3\delta )}$$
所以就得到了一开始我们写出的那个纳什均衡。

【例题】
某行业N个企业均以平均成本C生产同质产品，需求函数为:
$$p=a-b\left(\sum _{i=1}^n{q}_i\right)$$
如果N个企业中的F个是边缘企业，余下的K个组成一个联合群体。所有企业决定产量并寻求利润最大化，其中联合群体先决定群体的最优总产量，边缘企业在观察到联合群体的产量后各自同时决定自己的最优产量。则下列描述正确的有:
A.如果所有企业能构成一个联合群体，则$N\le 4$
B.如果所有企业能构成一个联合群体，则$N\ge 4$
C.两类群体企业数量不变化的条件为$$\frac{F^2+F+1}{F}\le K\le \frac{F^2+4F+4}{F+1}$$
D.市场稳定时应满足的条件为：
$$\frac{K^2+K+1}{K}\le F\le \frac{K^2+4K+4}{K+1}$$
【解】
(1)求纳什均衡。本博弈是完全信息的两阶段动态博弈，同时第二阶段又是一个完全信息静态博弈。运用逆推归纳法求解如下:
①第二阶段，F个企业在观察到联合群体总产量后同时决定产量，设每个企业的产量为$q_f(f=1,2,\dots \dots ，F)$，其得益函数为: $${\pi }_f=(p-c)q_f=\left[a-b\left(Q_K+\sum _{f=1}^F{q}_f\right)-c\right]q_f$$
由其一阶条件等于零有:即$\frac{d{\pi }_f}{d{q}_f}=0$得:$$a-b\left(Q_K+q_1+q_2+\cdots +q_{f-1}+2q_f+q_{f+1}\dots +q_F\right)-c=0$$所以反应函数为:
$$q_f=\frac{a-c}{2b}-\frac{1}{2}\left(Q_K+q_1+q_2+\cdots +q_{f-1}+q_{f+1}\dots +q_F\right)$$
记$$S=\frac{a-c}{b},Q_{F-f}=q_1+q_2+\cdots +q_{f-1}+q_{f+1}\dots +q_F\text{, 于是有 }{q}_f=\frac{S}{2}-\frac{1}{2}\left(Q_K+Q_{F-f}\right)=\frac{S-Q_K-Q_{F-f}}{2}$$
上述反应函数有F个，联立求得对称解为:
$$q_f=\frac{S-Q_k}{F+1}.....①$$
②第一阶段，设联合群体的总产量为$Q_k$，则联合群体得益函数为:
$$\begin{array}{rl}& {\pi }_K=(p-c)Q_K=\left[a-b\left(Q_K+\sum _{f=1}^F{q}_f\right)-c\right]Q_K.....②\\ & \text{ 将①带入②得: }{\pi }_K=\left[a-b\left(Q_K+\frac{F\left(S-Q_K\right)}{F+1}\right)-c\right]Q_K\\ & {\pi }_K=\left[a-b\frac{FS+Q_K}{F+1}-c\right]Q_K,\text{ 即 }{\pi }_K=b\left[\frac{a-c}{b}-\frac{FS+Q_K}{F+1}\right]Q_K\\ & {\pi }_K=b\left[S-\frac{FS+Q_K}{F+1}\right]Q_K,\text{ 即 }{\pi }_K=b\left[\frac{S-Q_K}{F+1}\right]Q_K\end{array}$$
由一阶条件等于零得:
$$b\frac{S-2Q_K}{F+1}=0\text{, 解得: }{Q}_K=\frac{S}{2}.....③$$将③带入①得:$q_f=\frac{S}{2(F+1)}$
于是得到纳什均衡解为:联合群体的每个企业生产$q_K=\frac{S}{2K}$,每个边缘企业生产$q_f=\frac{S}{2(F+1)}$
(2）确定边缘群体和联合群体企业数量不再变化，即市场稳定状态时应满足的条件。由(1）可得企业的得益:联合群体中每个企业的得益为$${\pi }_k(F,K)=\frac{b{S}^2}{4K(F+1)}$$
边缘企业的得益为$${\pi }_f(F,K)=\frac{b{s}^2}{4(F+1{)}^2}$$
若边缘群体和联合群体企业数量不再变化，意味着边缘企业进入联合企业之后边缘企业的利益会减少，联合企业进入边缘企业之后联合企业的利润会减少。则边缘企业也不愿意成为联合企业，联合企业也不愿意成为边缘企业。则需满足的条件为:
1)联合群体中的企业的得益大于出来成为边缘企业的得益，即:${\pi }_k(F,K)>{\pi }_f(F+1,K-1)$,于是有:$$\frac{b{S}^2}{4K(F+1)}>\frac{b{S}^2}{4(F+1+1{)}^2}\text{, 得 }K<\frac{F^2+4F+4}{F+1}.....④$$
2)边缘企业的得益大于进入联合群体后的得益，即:${\pi }_k(F-1,K+1)<{\pi }_f(F,K)$，于是有:$$\frac{b{S}^2}{4(K+1)(F-1)}<\frac{b{S}^2}{4(F+1{)}^2}\text{, 得 }K>\frac{F^2+F+2}{F-1}.....⑤$$
⑤
于是联合④⑤得到边缘群体和联合群体企业数量不再变化，即市场稳定状态时应满足的条件为:
$$\frac{F^2+F+2}{F-1}<K<\frac{F^2+4F+4}{F+1}$$
看题目中的选项：如果全部联合起来，则边缘企业数量$F=0$。则可以算出K是在2到4这个范围内。

重复博弈

重复博弈及其特点
重复博弈:同样结构的博弈重复多次,特殊的动态博弈

• 每次博弈称为阶段博弈(stage game)
• 分为有限次重复博弈和无限次重复博弈

由于长期利益的制约，一次博弈中不可信的威胁或许诺会变为可信，存在合作的可能性及更有效率的均衡。
博弈的均衡结果有多种可能性。影响博弈均衡结果的主要因素是博弈重复次数和信息的完备性(completeness)
子博弈完美性是判断均衡是否稳定可靠的依据。

有限次重复博弈

给定一个博弈G，重复进行T次G，并且在每次重复之前各参与人都能观察到以前博弈的结果，这样的博弈过程称为G的一个“T次重复博弈”，记为G (T)。而G则称为G(T)的原博弈。G (T)中的每次重复称为G(T)的一个阶段。

【例9】有限次零和博弈

猜硬币博弈:不会创造出任何新的利益，双方不存在合作的可能性，参与人的战略是在每次重复时都采用一次性博弈中所采用的纳什均衡战略，也即各以0.5的概率随机选正面和反面的混合战略。双方每次重复的平均期望得益和期望总得益都为0。
所有以零和博弈为原博弈所构成的重复博弈，各参与人的战略就是在每次重复中都采用一次性博弈中的纳什均衡战略。

【例10】唯一NE的有限次重复博弈，囚徒困境:重复两次

第二阶段:仍是困境博弈，实现自身在本阶段中的最大利益是两参与人在该阶段决策的唯一原则，结果就是原博弈的一次性博弈的NE（坦白，坦白)，双方得益为(-5，-5)。

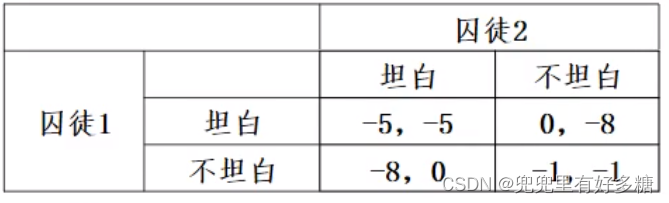
第一阶段，参与人对后一阶段出现的结果一清二楚，双方的最终得益就是在本阶段的得益上加-5。该等价博弈的唯一NE仍然是（坦白，坦白)，得益则为(-10，-10）。

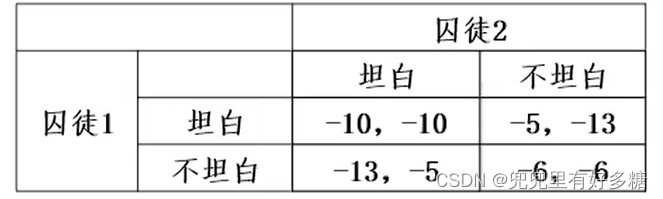
如果原博弈存在唯一的纯战略NE，则有限次重复博弈的均衡解即各参与人在每阶段都采用原博弈的NE（NE就是纳什均衡）。

定理:设原博弈G有唯一纯战略纳什均衡，则对任意正整数T,重复博弈G(T)有唯一的子博弈精练解，即各参与人每个阶段都采用G的纳什均衡战略。各参与人在G(T)中的总得益为在G中得益的T倍，平均每阶段得益等于原博弈G中的得益。

【思考】连锁店悖论

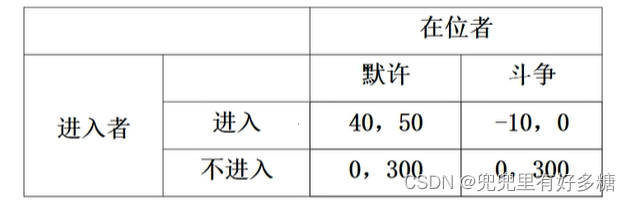
如果按上面的定理来解决这个问题发现是违背常理的，所以是不对的。所以这是一个悖论。
该博弈有唯一的子博弈精练纳什均衡（进入，默许)，得益为( 40，50）。
20次重复博弈:在位者有20个市场，进入者每次进入一个市场。
在位者倾向于选择对进入者进行斗争，从而获得300的收益，而不是采用原来的纳什均衡策略。

【例题】有两个NE的重复博弈

该博弈有两个纯战略纳什均衡$(A，B)$和$(B，A)$，得益分别为$(1,4)$和$(4,1)$。此外它还有混合战略纳什均衡，即厂商$1$和厂商$2$都以相同的概率在$A、B$之间随机选择，双方期望得益都等于$0.25\times (3+4+1+0)=2$。
两次重复博弈
轮换战略:厂商1在第一阶段去A，第二阶段去B;厂商2在第一阶段去B，第二阶段去A。均衡路径是第一次博弈（A，B)，第二次（B，A)。两次重复双方的每阶段平均得益是（4+1)/2=2.5，比采用混合战略期望得益高。
连续两次都出现原博弈的同一个NE:第一次是（A，B)，第二次还是（A，B）和第一次是(B，A)，第二次还是（B，A)。平均得益就分别是（1，4）和（4，l)。
两厂商两次重复都采用混合战略，双方平均期望得益都是2。
两次重复中，一次是纯战略NE(A，B)或(B，A)，另一次是混合战略均衡，双方(期望）得益为（ 1.5，3）和(3，1.5)

重复三次
厂商1:第一阶段选A;如果第一阶段结果是（A，A)，则第二阶段选A;如果第一阶段结果是（A，B)，则第二阶段选B;第三阶段无条件选B。
厂商2:第一阶段选A;第二阶段无条件选B;如果第一阶段结果是（A，A)，则第三阶段选A;如果第一阶段是（B，A），则第三阶段选B。
这条路径双方每阶段平均得益都为（3+1+4）/3=2.67，大于所有每阶段都采用原博弈的NE战略组合的路径所能取得的平均得益或平均期望得益。

过渡到无限次的时候就要采用新的模型了：

扳机战略（触发战略，trigger strategy;冷酷战略，grim strategy) :参与人首先试探合作，一旦发觉对方不合作则也用不合作相报复，利用有后续阶段博弈的制约作用达成均衡的战略。