前言引入:
假设现在有一个数组,我们需要不断地根据题意给出的Left 和 Right(区间)输出该数组的对应区间和。如a : {1,2,3,4,5} 令数组第一位置为0,当Left=1,Right=5时,答案为15。由于该数组只有五个数,哪怕是遍历一次求时间也极短。
int sum = 0;
for(int i = Left;i <= Right; i++)
{
sum + = a[i];
}
cout << sum;但是当我的Left=1,Right极限为2e5,以至于更大时。那么你还会选择遍历吗?好,你说遍历一次也不耗时间,那如果我让你查询N(2e5)次Left=1,Right=2e5时的区间和呢?好,你说单独定义一个sum记录一模一样的Left和Right,那如果我查询完一次又让你修改数组某一位置呢?不难发现,这种写法时间复杂度为O(N*N)。
在这里引入两种算法:树状数组和线段树。
本篇文章详解树状数组。
其建树复杂度:nlogn.
区间查询和单点修改:logn.
什么是树状数组:
在这里,树状数组是一个一维数组,其每一个位置上代表的值为为原数组中某一段区间和。
树状数组是用来干什么的:
如上文所言,树状数组可用于快速求区间和,同时可以完成另一项操作:对于数组的某单一位置进行修改并不影响后续区间和输出。即:
单点修改,区间查询
我们为什么称这个数组为 树状 数组呢?
对于一般数组而言,如下图为a : {1,2,3,4,5}。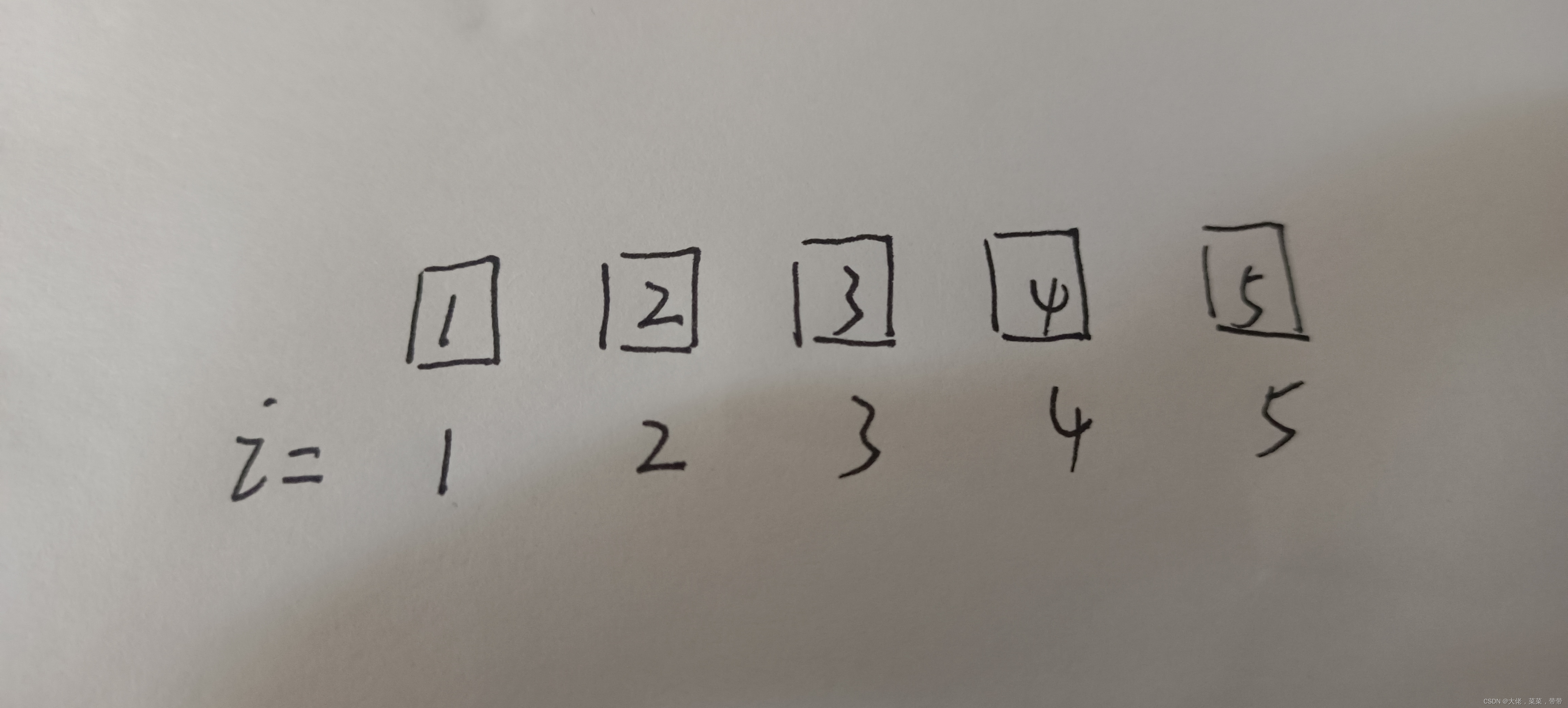
但是若用该数组建立一个树状数组,那么将会变成如下图:

我们所建立的数组tree并不和a对等,其中tree[1]=1,tree[2]=3,tree[3]=3,tree[4]=10,tree[5]=5.
由于其构图形似一颗树。
由于该图十分简单,我们可以直观的发现一些规律,我已经用箭头表示了出来:
比如tree[4]=10=tree[2]+tree[3]+a[4]=a[1]+a[2]+a[3]+a[4]。即树状数组存储的是某一段的区间和。我们可以发现,tree[4]是由所说a数组中四个数所影响到的,但是又看tree[3]又是直接由a[3]的值构成,但影响tree[4],而tree[5]为什么又不由先前数组所影响呢?可以看出对于数组数组tree[ids](ids为tree下标),该数组内容tree[ids]一定包含了a[ids]。其次,该数还受之前的tree[id]影响。
如ids=4时,tree[4]=tree[2]+tree[3]+a[4] ,ids=8时id= tree[6]+tree[4]+a[8]=a[1]+...+a[8]。(如下图)。即后来的tree受到先前的某一部分tree节点的影响,我们令下图中tree[8]为最后一层,那么该数的第二层如tree[2]=a[1]+a[2]。所有的该层节点都由其下方两数组成,将图稍微分开一点,不难看出其实就为二叉树。
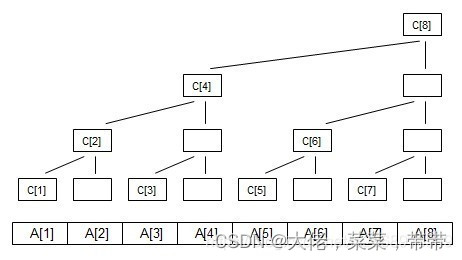
不要被迷惑了,其实总结一下对于每一个数a[id],它会影响到很多的tree[ids]。
左边的数会影响到右边的tree[id]。
我们之所以这么画图,是为了让你更好的看出其影响的规律。不然如果没有那么多空白的格子出来,所有的线都连到一个格子,那么就极其紊乱了(比如tree[8]我要是不画那么多空白格,那真的太棒了)。那么到底是影响哪些ids呢?
规律为lowbit函数所带来的值:
ll lowbit(ll x)
{
return x & (-x);//x&(~x+1)
}举几个个例子:
在a[1]影响的tree,其影响到的tree[ids]为 1(本身) 2 4 8.你看:
lowbit(1)=1;1+1=2;
lowbit(2)=2;2+2=4;
lowbit(4)=4;4+4=8;
在a[5]影响的的tree,其影响到的tree[ids]为5(本身) 6 8.你看:
lowbit(5)=1;5+1=6;
lowbit(6)=2;6+2=8;
在a[6]影响的的tree,其影响到的tree[ids]为6(本身) 8.你看:
lowbit(6)=2;6+2=8;
之所以到ids到8就停止是应为树状数组的建立边界同为原数组的边界,如上文所言,tree[ids]一定包含了a[ids],那么要是a[ids]都不存在,那么自然无法建立tree[ids]。

建树代码:
int a[N], tree[N], n;
int lowbit(int x)
{
return x & (-x);//x&(~x+1)
}
void build(int id)
{
while (id <= n)//右边界
{
tree[id] += a[id];
id += lowbit(id);
}
}
signed main()
{
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
build(i);
}
}我们发现,这个数组a其实毫无用处,我们只需要根据id不断更新tree就可以了,所以代码可以改为:
int tree[N], n;
int lowbit(int x)
{
return x & (-x);//x&(~x+1)
}
void update(int id, int num)
{
while (id <= n)//右边界
{
tree[id] += num;
id += lowbit(id);
}
}
signed main()
{
cin >> n;
int a;
for (int i = 1; i <= n; i++)
{
cin >> a;
update(i, a);
}
}这时候建树就建立完了。每一个tree[id]代表的意义也理解了。
是时候输出区间和了!
好了,那就试试区间Left=1,Right=8吧,明显,tree[8]就是答案,输出即可,但是要是Left=1,Right=5呢?(要是不记得了上去翻图)。
Left=1,Right=5很明显此时区间和为tree[5]+tree[4].
Left=1,Right=7,此时区间和应当为tree[7]+tree[6]+tree[4]
Left=1,Right=4,区间和就为tree[4]
Left=1,Right=8,区间和就为tree[8]
有了之前的Lowbit,不难发现这个区间和影响的也是lowbit
Left=1,Right=7,sum+=tree[7];
lowbit(7)=1;7-1=6;sum+=tree[6];
lowbit(6)=2;6-2=4;sum+=tree[4];
lowbit(4)=4;4-4=0;sum+=tree[0](0);
而如
Left=1,Right=8,sum+=tree[8];
lowbit(8)=8;8-8=0;sum+=tree[0](0);
其他同理。
但是如果Left并不是1呢?其实学到这里了已经不难发现了。
Left=3,Right=5;如果我们没有学树状数组,也知道使用前缀和的差值来算。
前缀和:
int ss[N];
int x[N];
signed main()
{
for (int i = 1; i <= n; i++)
{
cin >> x[i];
ss[i] = ss[i - 1] + x[i];
}
//此时的ss[i]表示的值为x[1]+x[2]+x[3]+...+x[i];
//如果我们要输出区间为left-right 的x区间和
cout << ss[right] - ss[left - 1] << endl;
}在树状数组同理使用前缀和:
区间查询:
int tree[N], n;
int lowbit(int x)
{
return x & (-x);//x&(~x+1)
}
void update(int id, int num)
{
while (id <= n)
{
tree[id] += num;
id += lowbit(id);
}
}
int query(int id)
{
int sum = 0;
while (id > 0)
{
sum += tree[id];
id -= lowbit(id);
}
return sum;
}
signed main()
{
cin >> n;
int a;
for (int i = 1; i <= n; i++)
{
cin >> a;
update(i, a);
}
int left, right;
cin >> left >> right;
cout << query(right) - query(left - 1) << endl;
//由于query中的while限制条件为id>0,意思就是求1-id的区间和
//那么query(right) - query(left - 1)就是left——right的区间和
}单点修改:
好了,现在题目要求你修改该数组中某一个位置的值,然后再让你输出后边的区间查询结果,那么怎么更新呢?我们已经理解了树状数组,明白原数组中的值只会由(lowbit)影响到后面部分tree的值,那么我们自然需要更改所有其影响到的tree[ids]。好说好说:
int tree[N], n;
int x[N];
int lowbit(int x)
{
return x & (-x);//x&(~x+1)
}
void update(int id, int num)
{
while (id <= n)
{
tree[id] += num;
id += lowbit(id);
}
}
signed main()
{
cin >> n;
int a;
for (int i = 1; i <= n; i++)
{
cin >> a;
update(i, a);
}
int id, num;
cin >> id >> num;
update(id, num);//把a[id]加上num
update(id, -num);//把a[id]减去num
//把a[id]改成num,这时候就需要保留原数组了
update(id, num - x[id]);
}最后注意数据范围看是否要开long long。
对于复杂度而言,由于Lowbit的关系,所以得证。
树状数组相对于线段树而言功能较少,但是代码简洁,在面对单点修改和区间查询问题时更优。
写这个东西真的很累,因为自己明白初学者刚见到树类数组时的不理解与无奈,所以写的时候就会大量的阐述想要解释明白。希望这篇能够帮到大家吧。
哈哈其实这篇文章是写给一个小屁孩的。嗷嗷嗷~~~~~~。