SVM(一)

一.什么是SVM

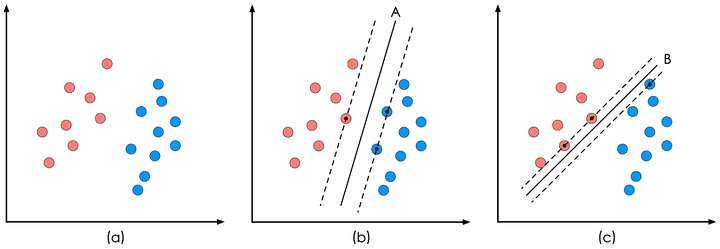
通俗来讲，SVM就是一个能把数据分的最开的lr，它也是构造一个线性分类超平面。能将两类数据分开的超平面有很多，lr是找出能让所有数据远离的超平面，而svm只专注于那些离超平面最近的点，因为这些点才是比较难分容易混淆的点。如下图，很自然的能

理解A比B要好，因为B中那些离分离面近的点我们不太确定属于哪类。

二.线性SVM

从第一节可以看到，svm优化的是决策面到离超平面最近点的距离，这里提出函数间隔和几何间隔

函数间隔： y(wTx + b) = yf(x)
函数间隔y*f(x)可以表示分类正确性和分类确定性(大小和正负)，但是这只能相对的表示大小，如果成比例的改变w和b的大小，函数间隔也会改变，因此提出几何间隔。

几何间隔：

比起函数间隔，我们更想知道这些数据点到分离平面的距离，也就是点到直线的距离，下面就是点到直线的距离公式

$d = \frac{|\boldsymbol{\omega}^T\boldsymbol{x}+\gamma|}{||\boldsymbol{\omega}||}$

距离公式仍旧有一些问题，比如不能表示样本点分类正确性，我们的目的只是让支持向量的样本点到分离面的距离最小而不是全部的点。我们将y标签分为+1，-1(此处取任意两个数也可以，但是取+-1是为了计算方便且可表示函数结果的正负)，那么分类：

$\left\{\begin{array}{ll} \boldsymbol{\omega}^T\boldsymbol{x}_i+\gamma>0 & \textrm{for~~} y_i=1\\\boldsymbol{\omega}^T\boldsymbol{x}_i+\gamma<0 & \textrm{for~~} y_i=-1\end{array}\right.$

假设现在已经找到了决策面，该决策面应该是在间隔区域中间，支持向量到决策面的距离为d，那么上式可写成

$\left\{\begin{array}{ll} (\boldsymbol{\omega}^T\boldsymbol{x}_i+\gamma)/||\boldsymbol{\omega}||\geq d & \forall~ y_i=1\\(\boldsymbol{\omega}^T\boldsymbol{x}_i+\gamma)/||\boldsymbol{\omega}||\leq -d & \forall~y_i=-1\end{array}\right.$

将上式左右除以d后变为下式，注意此时的w和r已经不是上式的w和r了，而是除以||w||*d之后了

$\left\{\begin{array}{ll} \boldsymbol{\omega}^T\boldsymbol{x}_i+\gamma\geq 1 & \textrm{for~~} y_i=1\\\boldsymbol{\omega}^T\boldsymbol{x}_i+\gamma\leq -1 & \textrm{for~~} y_i=-1\end{array}\right.$

统一化表达成 $y_i(\boldsymbol{\omega}^T\boldsymbol{x}_i+\gamma)\geq 1~\forall \boldsymbol{x}_i$ ，这是约束条件。

由于我们要优化的是支持向量到分离面的距离，那么支持向量应该满足 $\boldsymbol{\omega}^T\boldsymbol{x}_i+\gamma= 1~~\textrm{or}~~-1$ ，带入到直线距离公式d中可得 $d = \frac{|\boldsymbol{\omega}^T\boldsymbol{x}_i+\gamma|}{||\boldsymbol{\omega}||}=\frac{1}{||\boldsymbol{\omega}||},~~\textrm{if} ~\boldsymbol{x}_i \textrm {is a support vector}$ ，最大化d即是最小化w，整理得优化目标函数：

$\begin{array}{l} \min_{\boldsymbol{\omega},\gamma}\frac{1}{2}||\boldsymbol{\omega}||^2\\ ~\\ \textrm{s. t.}~ ~y_i(\boldsymbol{\omega}^T\boldsymbol{x}_i+\gamma)\geq 1,~~i = 1,2,...,m \end{array}$

猜你喜欢