欧拉函数

初步认识：

在数论，对正整数n，欧拉函数是小于n的正整数中与n互质的数的数目（φ(1)=1）。此函数以其首名研究者欧拉命名(Euler's totient function)，它又称为Euler's totient function、φ函数、欧拉商数等。 例如φ(8)=4，因为1,3,5,7均和8互质。 从欧拉函数引伸出来在环论方面的事实和拉格1.

通式：

其中p1, p2……pn为x的所有质因数，x是不为0的整数。

φ(1)=1（和1互质的数(小于等于1)就是1本身）。

注意：每种质因数只一个。 比如12=2*2*3那么φ（12）=12*（1-1/2）*(1-1/3)=4

若n是质数p的k次幂，

，因为除了p的倍数外，其他数都跟n互质。

设n为正整数，以 φ(n)表示不超过n且与n互素的正整数的个数，称为n的欧拉函数值

φ：N→N，n→φ(n)称为欧拉函数。

欧拉函数是积性函数——若m,n互质，

特殊性质：当n为奇数时，

, 证明与上述类似。

若n为质数则

对于素数p, φ(p)=p-1，对于对两个素数p,q φ（pq）=pq-1朗日定理构成了欧拉定理的证明。

求法模板：

int ou_lar( )
{
    int i , j, k;
    memset( enlur, 0, sizeof( enlur ));
    memset( visit  , 0, sizeof( visit ));
    visit[1] = 1;
    enlur[1] = 0;
    for( i = 2; i<=1000005; i++)
    {
        if( !enlur[i] )
        {
            visit[i] = 1;
            enlur[i] = i-1;
            for( j = 2*i; j <= 1000005; j = j+i)
            {
                if( !visit[j] )
                {
                    enlur[j] = j;
                    visit[j] = 1;
                }
                enlur[j] = enlur[j]/i*( i-1 );
            }
        }
    }
}

例题跟踪：

A - Bi-shoe and Phi-shoe

 LightOJ - 1370 

Bamboo Pole-vault is a massively popular sport in Xzhiland. And Master Phi-shoe is a very popular coach for his success. He needs some bamboos for his students, so he asked his assistant Bi-Shoe to go to the market and buy them. Plenty of Bamboos of all possible integer lengths (yes!) are available in the market. According to Xzhila tradition,

Score of a bamboo = Φ (bamboo's length)

(Xzhilans are really fond of number theory). For your information, Φ (n) = numbers less than n which are relatively prime (having no common divisor other than 1) to n. So, score of a bamboo of length 9 is 6 as 1, 2, 4, 5, 7, 8 are relatively prime to 9.

The assistant Bi-shoe has to buy one bamboo for each student. As a twist, each pole-vault student of Phi-shoe has a lucky number. Bi-shoe wants to buy bamboos such that each of them gets a bamboo with a score greater than or equal to his/her lucky number. Bi-shoe wants to minimize the total amount of money spent for buying the bamboos. One unit of bamboo costs 1 Xukha. Help him.

Input

Input starts with an integer T (≤ 100), denoting the number of test cases.

Each case starts with a line containing an integer n (1 ≤ n ≤ 10000) denoting the number of students of Phi-shoe. The next line contains n space separated integers denoting the lucky numbers for the students. Each lucky number will lie in the range [1, 106].

Output

For each case, print the case number and the minimum possible money spent for buying the bamboos. See the samples for details.

Sample Input

3

5

1 2 3 4 5

6

10 11 12 13 14 15

2

1 1

Sample Output

Case 1: 22 Xukha

Case 2: 88 Xukha

Case 3: 4 Xukha

/////互质即只有公因数1；若n为素数 则欧拉值即为 n-1

/题意  竹子长度为k 得分为小于等于k并且与k互质的数的个数
///即为欧拉函数的值 ， 现在给定n个幸运数字 要求所买竹子的得分必须大于等于
///对应的数字 并且单位长度为1元 求最小花费

///思路 : 欧拉函数打表 ， 要想得分大于等于n  则竹子长度必须大于等于n
///即逐渐找欧拉函数值大于n的相加
 

///tip; 本题是小于n的与n互质的个数  所以1时为0 其余不变

代码

#include<cstdio>
#include<cstring>
#include<map>
#include<algorithm>
#include <queue>
using namespace std;
int enlur[1000005];
int visit[1000005];
int ou_lar( )
{
    int i , j, k;
    memset( enlur, 0, sizeof( enlur ));
    memset( visit  , 0, sizeof( visit ));
    visit[1] = 1;
    enlur[1] = 0;
    for( i = 2; i<=1000005; i++)
    {
        if( !enlur[i] )
        {
            visit[i] = 1;
            enlur[i] = i-1;
            for( j = 2*i; j <= 1000005; j = j+i)
            {
                if( !visit[j] )   以便赋初值
                {
                    enlur[j] = j;
                    visit[j] = 1;
                }
                enlur[j] = enlur[j]/i*( i-1 );
            }
        }
    }
}

int main()
{
    int t;
    ou_lar();
    scanf("%d", &t);
    int cn = 1;
    int n , m;
    int i , j;
    while( t-- )
    {
        long long int sum = 0;
        scanf("%d", &n);
        for( i = 0; i<n; i++)
        {
            scanf("%d", &m);
            for( j = m; j; j++)
            {
                if( enlur[j] >= m )
                {
                    sum = sum + j;
                    break;
                }
            }
        }
        printf("Case %d: %lld Xukha\n", cn++, sum);
    }
    return 0;
}

唯一分解定理

算术基本定理（唯一分解定理）

一句话： 
　　　

认识：　 
任何大于１的自然数，都可以唯一分解成有限个质数的乘积

例如对于大于1的自然数n，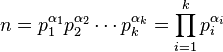 
 
这里P均为质数，其指数a是正整数。 
这样的分解称为的标准分解式。

唯一分解定理的基本应用：

① 一个大于1的正整数N，将其化成标准分解式N = p1^a1 * p2^a2 *....pn^an(例如24 = 2^3 * 3^1),那么N的正因数个数为σ1(N) = (a1+1)*(a2+1)*....(an+1)（ 因子各不相同）

（p1..pn为N的素因子，a1...an为各素数的幂）

② 所有正因数之和为σ2 = （1+p1+p1^2+...p1^a1）* (1+p2+p2^2+....p2^a2) * ..... *(1+pn+pn^2+.....pn^an);当σ2（N） = 2*N时称N为完全数，是否存在奇完全数，尚不明确

③ 利用算数基本定理可以重新定义a和b的最大公因子（a,b）和最小公倍数（a,b）， a*b= 最大公因子（a,b）* 最小公倍数（a,b）

 唯一分解定理模板

typedef long long ll;
ll fac[10050], num;//素因数,素因数的个数
void init(ll n) {//唯一分解定理
    num = 0;
    ll cpy = n;
    int m = (int)sqrt(n + 0.5);
    for (int i = 2; i <= m; ++i) {
        if (cpy % i == 0) {
            fac[num++] = i;
            while (cpy % i == 0) cpy /= i;
        }
    }
    if (cpy > 1) fac[num++] = cpy;
}